Побудова графіків тригонометричних функцій у середовищі табличного процесора Місrosoft Еxcel та дослідження їх властивостей.

Про матеріал

Метою даного уроку є:  закріпити знання про табличні дані і графіки, вміння візуального аналізу даних, користування Майстром побудови діаграм при побудові графіків;  знати властивості тригонометричних функцій у=sin(x), y=cos(x), y=tg(x), y=ctg(x) навчитися будувати їх графіки;  продовжувати роботу по формуванню і розвитку дослідницьких навиків учнів;  здобувати стійкі навички роботи при побудові графіків в Excel;  розвивати алгоритмічний стиль, логічність, нестандартність мислення; уміння застосовувати знання для побудови та дослідження графіків тригонометричних функцій;  забезпечити розвиток аналітичного мислення на етапі засвоєння теоретичних знань;  уміти порівнюваним на етапі практичної обробки результати побудови;  виробляти навички аналізу та синтезу під час дослідження графіків тригонометричних функцій;  підтримувати постійну зацікавленість предметами, мотивувати засвоєння нових знань;  виховувати культуру мовлення, уміння чітко висловлювати свої думки;  формувати цілісне сприйняття світу через єдність законів природи на прикладі між курсових і міжпредметних зв’язків;акуратність та уважність при побудові графіків;  навички самостійності й самоаналізу в роботі з електронними пристроями обробки інформації;

Перегляд файлу

10 клас

Тема: Побудова графіків тригонометричних функцій у середовищі табличного процесора Місrosoft Еxcel та дослідження їх властивостей.

Мета:

навчальна:

закріпити знання про табличні дані і графіки, вміння візуального аналізу даних, користування Майстром побудови діаграм при побудові графіків;
знати властивості тригонометричних функцій у=sin(x), y=cos(x), y=tg(x), y=ctg(x) навчитися будувати їх графіки;
продовжувати роботу по формуванню і розвитку дослідницьких навиків учнів;
здобувати стійкі навички роботи при побудові графіків в Excel;

розвивальна:

розвивати алгоритмічний стиль, логічність, нестандартність мислення; уміння застосовувати знання для побудови та дослідження графіків тригонометричних функцій;
забезпечити розвиток аналітичного мислення на етапі засвоєння теоретичних знань;
уміти порівнюваним на етапі практичної обробки результати побудови;
виробляти навички аналізу та синтезу під час дослідження графіків тригонометричних функцій

виховна:

підтримувати постійну зацікавленість предметами, мотивувати засвоєння нових знань;
виховувати культуру мовлення, уміння чітко висловлювати свої думки;
формувати цілісне сприйняття світу через єдність законів природи на прикладі між курсових і міжпредметних зв’язків;акуратність та уважність при побудові графіків;
навички самостійності й самоаналізу в роботі з електронними пристроями обробки інформації;

Тип уроку: комбінований ( із елементами дослідження) .

Матеріально-технічне оснащення уроку:

мультимедійна дошка, персональні комп’ютери;програмне забезпечення: ОС Windows, офісний пакет програм Microsoft Excel;
картки з завданнями;(Додаток 3)
Пам’ятка№1 «Алгоритм побудови графіка функції» (Додаток1);
Пам’ятки №2 і №3 «Геометричні перетворення графіків функцій» (Додаток 2)

План уроку

І. Організаційний момент

1.1 Вступне слово вчителя.

1.2 Оголошення теми та мети уроку ( на проекторній дошці написаний текст ,який відображає тему та мету уроку)

ІІ. Актуалізація опорних знань учнів

(Опитування з елементами демонстраційних прикладів)

2.1 Побудова графіків елементарних тригонометричних функцій в Excel . Властивості тригонометричних функцій.

2.2.1. Бліц-опитування.

2.2.2. Демонстраційні приклади.

2.2.3 Перетворення графіків функції( опитування , демонстраційні приклади).

ІІІ. Мотивація вивчення теми.

ІV. Закріплення знань

V. Оцінювання знань та умінь.

VІ. Домашнє завдання.

Заключне слово вчителя:

Хід уроку

І. Організаційний момент

1.1 Вступне слово вчителя.

Доброго дня всі присутнім. Сьогодні ми на уроці спробуємо використати знання і вміння з двох предметів з інформатики та алгебри. З інформатики по темі : «Побудова графіків за допомогою табличного процесора Excel» та з алгебри по темах : «Тригонометричні функції та їх властивості» та «Перетворення графіків функцій»

1.2 Оголошення теми та мети уроку ( на проекторній дошці з’являється текст ,який відображає тему та мету уроку)

Вчитель озвучує тему та мету уроку.

ІІ. Актуалізація опорних знань учнів

(Опитування з елементами демонстраційних прикладів)

2.1 Побудова графіків елементарних тригонометричних функцій в Excel . Властивості тригонометричних функцій.

2.2.1. Бліц-опитування:

Запитання:

1. Що таке Еxcel?

2. Що таке графік у Microsoft Excel?

3. Які тригонометричні функції ви вивчали на уроках алгебри?

2.2.2. Демонстраційні приклади: (вчитель викликає по одному учнів , для демонстрації побудови на проекторній дошці та для характеристики властивостей елементарних тригонометричних функцій, всі інші учні будують за вказаним алгоритмом графіки у себе на ПК. При побудові, озвучується алгоритм побудови графіка функції в середовищі Excel, який на окремих аркушах знаходиться на робочих столах учнів.( Додаток 1))

Алгоритм побудови графіка функцій на прикладі функції у= sin(x).
Властивості графіка функції у=sin(x).
Побудова графіка функцій y=cos(x),( Приклад рис.1).
Властивості функції у=сos(x).
Побудова графіка функції y=tg(x).
Властивості графіка функції y=tg(x).

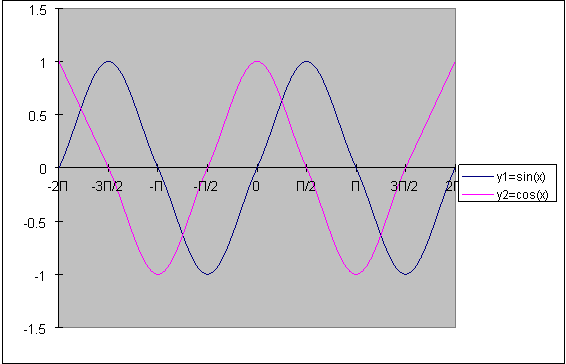
Рис. 1. Графіки функцій у=sin i y=cos x

2.2.3. Перетворення графіків функції. ( Кожен учень попередньо готує Пам’ятку про правила перетворення графіків елементарних функцій. Кожен, хто виходить до дошки розповідає їх, наводить приклад і роздає картки з правилами всім учням в класі. Вчитель викликає до дошки учнів, які наводять приклади складних тригонометричних функцій, і вказують правила за якими можна побудувати графік таких функцій, до кожного написаного прикладу викликається учень, який демонструє побудову графіків в одній системі координат. Кожен з присутніх виконує побудову на ПК.)

Проблемно-пошукова бесіда:

Які перетворення графіків функції ви знаєте? Наведіть приклади і запишіть їх на дошці

Демонстрація записаних прикладів.

Побудувати в одній системі координат записані приклади.

(Приклад рис.2.)

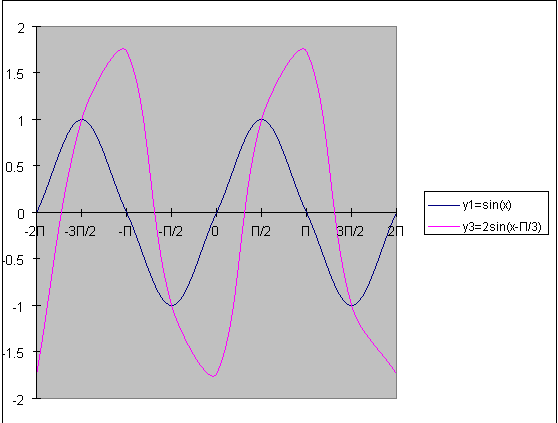
Рис.2 . Графік функції у=sinx та у=2 sin(x-π/3)

ІІІ. Мотивація вивчення теми.

Отже ми пригадали функції, їх властивості та алгоритми їх побудови.

Давайте розглянемо функцію у= 2 cos (x/2-П/6). Можливо хтось пам’ятає як ви здійснювали побудову такого графіка на уроках алгебри?

Ви здійснювали перетворення , які саме? (Викликається учень , який вказує послідовність побудови графіків і перетворення:

1) будуємо графік функції y₁=cosx; 2) y₂=cos1/2x; 3) y₃=2cos1/2x; 4)y₄=cos(1/2(x-π/3));4) y₁=2cos(1/2(x-π/3)+1 ).

Демонстрація учителем: (Вчитель будує на проекторній дошці всі графіки Рис.3-Рис.5) .

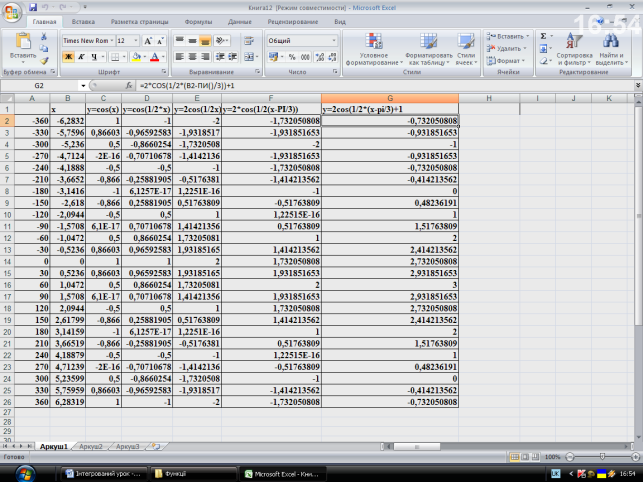
Рис.3. Таблиця , яка відображає перетворення графіка функції у=cos(x) в графік y=2cos(1/2*(x-pi/3)+1

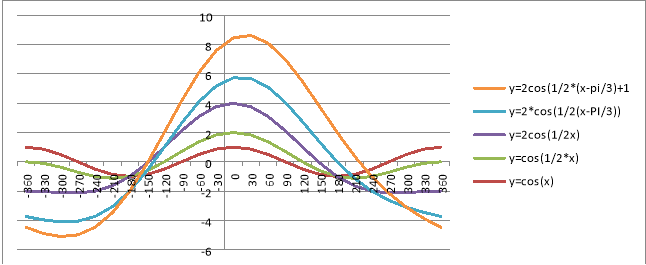
Рис.4. Графіки функцій, які відображають перетворення у=cos(x) в графік y=2cos(1/2*(x-pi/3)+1

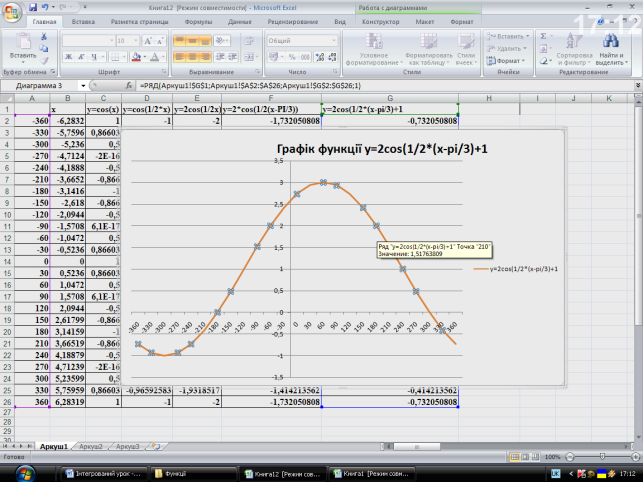
Рис.5. Графіки функцій y=2cos(1/2*(x-pi/3)+1

Якщо побудувати ці графіки в одній системі координат, використовуючи Excel? То ми побачимо всі перетворення і зрозуміємо складність побудови таких графіків на уроках алгебри.

Складності побудови ми не помітимо якщо побудувати в табличному процесорі лише графік у= 2 cos (x/2-П/6) (всі інші графіки забираються з поля побудови).

За графіком можна його дослідити: вказати область значень функції, область визначення , мінімуми і максимуми, проміжки зростання і спадання, проміжки знакосталості. (Вчитель показує на даному прикладі, як це зробити). Отже, ми з вами переконалися на власному досвіді, що використовуючи програмні засоби ми можемо швидше побудувати графік функції, зробити аналіз перетворень, дослідити функцію, але це все можливо, якщо знати і вміти застосовувати знання з алгебри та володіти знаннями і навичками роботи з комп’ютером. Зараз для того, щоб краще засвоїти матеріал уроку, ви виконаєте самостійну роботу.

ІV. Закріплення знань – виконання практичних завдань, відповідно до заданого варіанту(Додаток 3).

V. Оцінювання знань та умінь.

(Вчитель дякує за урок. Просить учнів не розчаровуватися, якщо не все вдалося . Відмічає роботу кожного і оцінюючи його роботу, наголошуючи на тому, що коли відбуваються якісь конкурси, то переможцям вручаються нагороди, а в нас нема переможців і переможених , тому нагородою буде домашнє завдання. Кожен отримує картку з домашнім завданням, щоб ті хто знає закріпили знання, а ті , хто не добре засвоїв, навчилися.)

VІ. Домашнє завдання.

Побудувати графік функції y=3/2-2sin(3x+П/4) в середовищі Еxcel або на папері. Дослідити властивості функції за графіком.

VII. Заключне слово вчителя:

Мені б хотілося закінчити заняття ось такими словами

Є. Долматовського ( на дошці відображуються поезія). Я озвучу їх мовою оригіналу:

Научись беду встречать не плача:
Горький миг – не зрелище для всех.
Знай: душа растет при неудачах
И слабеет, если скор успех.
Мудрость обретают в трудном споре.
Предначертан путь нелегкий твой
Синусоидой радости и горя,
А не вверх взмывающей кривой.

Евгений Долматовский

Додаток 1

Пам’ятка 1

Алгоритм побудови графіка функції

Побудувати таблицю значень функції, задавши інтервал з області визначення функції та крок зміни аргументу.
Виділити побудовану таблицю.
Завантажити Майстер діаграм.
На вкладці Нестандартні вибрати тип графіка Гладкі графіки.
Перевірити діапазон даних.
Вказати назву діаграми , назви осей.

При необхідності вилучити Лінії сітки.

Вибираємо розміщення графіка.
Клацаємо кнопкою Майстра діаграм Готово.
За допомогою контекстного меню відредаговуємо підписи осей та їх розміщення.

Додаток 2

Пам’ятка 2

Паралельне перенесення графіків

Вздовж осі ординат

Для побудови графіка функції g(x)=f(x)+a необхідно :

Побудувати графік функції f(x);
Перенести його на вектор k (0,а) вздовж осі ординат ,

якщо а>0 – вгору, і – вниз , при а<0.

Вздовж осі абсцис

Для побудови графіка g(x)=f(x+a) необхідно:

Побудувати графік функції f(x);
Перенести його на вектор k (-а,0),

якщо a>0 - вліво, і якщо а<0 – вправо.

Пам’ятка 3

Розтяг і стиснення графіків

До осі абсцис

Для побудови графіка g(x)=a f(x) необхідно:

Побудувати графік функції f(x);
Розтягнути до осі абсцис в а раз , якщо а>1
або стиснути до осі абсцис, якщо 0<a<1 в 1/а раз.

До осі ординат

Для побудови графіка g(x)=f( ) необхідно :

Побудувати графік функції f(x);
Розтягнути від осі ординат в а раз , якщо а>1

або стиснути до осі ординат, якщо 0<a<1 в 1/а раз.

Додаток 3

Завдання для самостійного виконання

Практичне завдання

Прізвище, ім’я учня_________________ клас_______

Варіант №1

Побудувати графіки функції відобразивши всі перетворення:

а)y=7 cos x , [-3П;3П] ,k= П/6;

б)y=tg(3x-7) [-3П;3П] ,k= П/6

Визначити:

1. Область значень функції а)________________________________________________________

б)________________________________________________________

2. Максимуми функції а)________________________________________________________

б)________________________________________________________

3.Мінімуми функції а)________________________________________________________

б)________________________________________________________

4. Проміжки зростання функції на заданому інтервалі а)________________________________________________________

б)________________________________________________________

Практичне завдання

Прізвище учня_________________ клас_______

Варіант №2

Побудувати графіки функції відобразивши всі перетворення:

а) y = 9sin х , [-3П;3П] ,k= П/6;

б)y= 2 sin(3x-П/3), [-3П;3П] ,k= П/6