Тема заняття: Поняття перпендикуляра, похилої та її проекції на площину.

Мета заняття: навчальна:

• сформувати поняття перпендикуляра до площини; похилої; проекції похилої на площину; відстань від точки до площини;
• установити взаємозв’язок між довжинами похилих, проведених з однієї точки до площини, і довжинами їхніх проекцій на площину.

розвиваюча:

• розвивати вміння застосовувати здобуті знання у побуті і для розв’язування задач.
• розвивати вміння розпізнавати вивчені фігури на моделях і рисунках;
• розвивати просторову уяву, логічне мислення, пам’ять. виховна:
• виховувати активність, самостійність, Тип заняття: заняття засвоєння нових знань.

Епіграф. Предмет математики такий серйозний, що корисно не нехтувати нагодою робити його трохи цікавим.

О.М. Крилов

Хід заняття

І. Організаційний момент.

ІІ. Актуалізація опорних знань і вмінь студентів.

Який розділ геометрії ми вивчаємо і який планіметричний матеріал вам необхідно було повторити? (Перпендикулярність прямих і площин в просторі. На домашнє завдання нам потрібно було повторити поняття перпендикуляра і похилої, проведених до прямої, ознаки подібності трикутників, а також розв’язати задачі.

На сьогоднішньому занятті ми з вами вивчимо поняття перпендикуляра і похилої до площини, тобто здобудемо нові знання і будемо вчитися застосовувати їх до розв’язування задач, продовжувати розвивати просторову уяву, працювати з моделями і з вашою допомогою зробимо серйозний урок математики цікавим.

 Фронтальне опитування.

1. Сформулюйте означення перпендикулярних прямих.
2. Дайте означення прямої, перпендикулярної до площини.
3. Сформулюйте ознаку перпендикулярності прямої та площини.
4. Скільки прямих, перпендикулярних до даної площини, можна провести через дану точку? ( Через будь-яку точку простору проходить пряма , перпендикулярна до даної площини і до того ж тільки одна )
5. Пряма перпендикулярна до двох сторін трикутника і проходить через його вершину. Чи перпендикулярна ця пряма до площини трикутника?
6. Пряма а перетинає площину α і перпендикулярна до прямої b, яка лежить у цій площині. Чи може пряма а не бути перпендикулярною до площини α?
7. Точка S лежить поза площиною ромба АВСD, причому SВ  ВС,

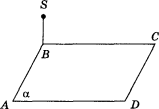SВ  АВ,  ВАD = 60°. Які з наведених тверджень правильні, а які – неправильні

1. пряма SВ перпендикулярна до площини АВС;
2. пряма АВ перпендикулярна до площини SВС;

3. пряма ВС перпендикулярна до площини АSВ;
4. пряма SВ перпендикулярна до прямої ВD?

8. Точка S лежить поза площиною трикутника АВС, причому SА  АС,

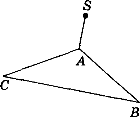АВ  АС, SА = SВ = АВ. Які з наведених тверджень правильні, а які - неправильні

1. пряма SА не перпендикулярна до площини АВС;
2. пряма АВ перпендикулярна до площини SАС;
3. пряма АС перпендикулярна до площини SАВ;
4. пряма ВС перпендикулярна до площини АSС?

 Математичний диктант

Дано прямокутний паралелепіпед АВСDMNKL . АВСD – квадрат. Користуючись зображенням, запишіть:

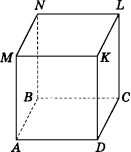1. площину, яка проходить через точку М прямої АМ і перпендикулярна до неї;
2. пряму, яка перпендикулярна до площини АВС і проходить через точку D;
3. пряму, яка перпендикулярна до площини АВС і проходить через точку N;
4. площину, яка перпендикулярна до прямої ВD;
5. прямі, які перпендикулярні до площини АМС;
6.   площини, які перпендикулярні до прямої DС. Відповіді:

1) (MNK); 2) KD; 3) BN; 4) (ACM); 5) BD і KN; 6) (ADK) і (BCL).

 Повторення планіметричного матеріалу.

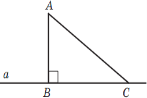1. Що ви бачите на даному рисунку?
2. Як називають відрізок АВ?
3. А як ще називають довжину відрізка АВ ?
4. Як називають відрізок АС?
5. Як називають точку В, точку С?
6. Як називають відрізок ВС?
7. Як знайти відстань від точки А до прямої а ?
8. Скільки перпендикулярів можна провести з даної точки до даної прямої?
9. Скільки похилих можна провести з даної точки до даної прямої?
10. Скільки рівних похилих можна провести з даної точки до даної прямої?
11. Якщо до прямої з однієї точки проведені перпендикуляр і похила, то що більше: перпендикуляр чи похила?
12. Якщо похилі, проведені з однієї точки до даної прямої, рівні, то що можна сказати про їх проекції?
13. Якщо проекції у похилих різні, то яка похила буде більша?

ІІІ. Вивчення нового матеріалу.

А зараз давайте дамо означення перпендикуляра до площини, похилої до площини, її проекції на площину і сформулюємо властивості перпендикуляра і похилої, а також означимо поняття відстані від точки до площини.

Запишемо тему сьогоднішнього заняття: «Поняття перпендикуляра, похилої та її проекції на площину.»

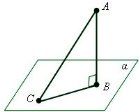Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.

Кінець цього відрізка, що лежить у площині, називається

основою перпендикуляра.

Довжина перпендикуляра називається відстанню від даної точки до площини .

На малюнку: АВ – перпендикуляр, точка В – основа перпендикуляра.

Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини.

На малюнку: АС – похила.

Відрізок ВС, який сполучає основи перпендикуляра та похилої, проведених з однієї і тієї самої точки, називають проекцією похилої АС у площині α.

 Чи існує залежність між довжинами перпендикуляра й похилої, похилої та її

 проекції?

Відповідь дає така теорема.

Теорема (властивості перпендикуляра й похилої)

Якщо з точки, взятої поза площиною, проведено до площини перпендикуляр і похилі, то:

1. перпендикуляр коротший за будь-яку похилу;
2. проекції рівних похилих є рівними й, навпаки, похилі, що мають рівні проекції, є рівними;
3. з двох похилих більша та, проекція якої більша.

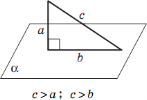
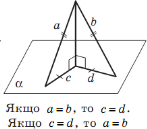
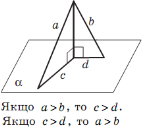
Всі розглянуті властивості випливають з теореми Піфагора і, на відміну від площини, де з даної точки до прямої можна провести скільки рівних похилих? ( тільки дві), а у просторі? (у просторі з точки до площини можна провести нескінченну множину рівних похилих.

ІV. Формування вмінь та відпрацьовування навичок.

Усні вправи

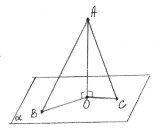
1.З точки М, що не належить площині, проведені дві похилі МВ і МА та перпендикуляр МО.

1)  Яка точка є проекцією точки М?

2)  Назвіть відрізок, довжина якого дорівнює відстані від точки М до площини α.

3) Якщо МА = 9 см, МВ = 12 см, то яка проекція буде більша?

4)  Якщо ОА = 3 см, ОВ = 1 см, то яка похила більша?

5)  Якщо МА : МВ = 5 : 6, то яка проекція буде менша?

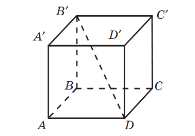
2. Дано куб АВСDA'B'C'D'.

Укажіть проекцію діагоналі B'D на площину:

а) АВС;

б) ВВ'С';

Письмові вправи

Розв’язання простіших задач на похилу та її проекцію на площину  зводиться до розв’язання прямокутного трикутника, сторонами якого є похила, її проекція на площину і перпендикуляр до площини.

Якщо такого трикутника немає на малюнку, то, щоб його утворити, проводимо допоміжні відрізки.

Задача 1. Знайдіть довжину похилої, якщо довжина перпендикуляра дорівнює 6 см, а проекції похилої на площину – 8 см.

Задача 2. Знайдіть довжину перпендикуляра, якщо довжина похилої становить 17 см, а її проекції на площину – 15 см.

Задача 3. З вершини С квадрата АВСD проведено перпендикуляр СМ до його площини. Знайдіть відстань АМ, якщо СМ дорівнює 6 см, а сторона квадрата - 4 см.

Розв’язання.

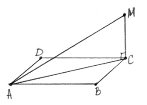Проведемо діагональ АС квадрата АВСD.  ∆АСМ – прямокутний,  оскільки СМАС за означенням перпендикулярності прямої і площини.

За даною стороною квадрата знаходимо його діагональ:

АС = АD = 4∙∙ = 8 см.

З ∆АСМ за теоремою Піфагора матимемо:

АМ = см.

Відповідь:  АМ = 10 см.

Якщо в задачі йдеться про дві похилі, проведені з однієї точки до площини, то розглядаємо два прямокутних трикутники, спільним катетом яких є перпендикуляр, опущений з даної точки на площину.

Задача 4.  З точки до площини проведені дві похилі, які дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть відстань від даної точки до площини.

Розв’язання.

Нехай  АС = 10 см,  АВ = 17 см  і  СО:ОВ = 2:5.  Позначимо проекції похилих СО = 2х  і  ОВ = 5х. З прямокутних трикутників АОС і АОВ знаходимо АО².

З ∆АОС: 

АО² = АС² – СО² = 102 – (2х)² = 100 – 4х².

З ∆АОВ:

АО² = АВ² – ОВ² = 172 – (5х)² = 289 – 25х².

Дістанемо рівняння:  100 – 4х² = 289 – 25х²;

                                     21х² = 189;

                                     х² = 9.

Отже, АО = см.

Відповідь:  АО = 8 см.

Якщо дано кілька рівних похилих, проведених з точки до площини, то їх кінці лежать на колі, центром якого є основа перпендикуляра, опущеного на площину зі спільної точки похилих.

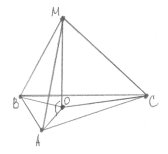
Задача 5.  З даної точки до площини проведено три рівні похилі довжиною 14 см. Відстані між кінцями похилих дорівнюють 9 см. Знайдіть відстань від даної точки до площини.

Розв’язання.

Нехай МА = МВ = МС = 14 см, АВ = ВС = АС = 9 см. Проведемо перпендикуляр МО до площини α. ОА = ОВ = ОС  

як проекції рівних похилих. Тому точка О – центр кола, яке проходить через кінці цих похилих. Знайдемо радіус кола, описаного навколо рівностороннього трикутника АВС.

R = см.

Із прямокутного трикутника МОС за теоремою Піфагора дістанемо:

МО = см.

Відповідь: МО = 13 см.

V. Підсумок заняття.

                             Кросворд.

1. Найкоротша відстань від точки до площини. (Перпендикуляр)
2. Похилі, які мають рівні проекції,   ……….  . (Рівні)
3. Трикутник це геометрична    ……….  . (Фігура)
4. Кінець перпендикуляра, що лежить у площині. (Основа)
5. Одна із сторін прямокутного трикутника. (Гіпотенуза)
6. Відрізок, який сполучає дану точку, з точкою площини, але не перпендикуляр. (Похила)
7. Відрізок, що сполучає основи перпендикуляра і похилої, проведених з однієї точки. (Проекція)

Ключове слово:  ПІФАГОР.

VІ. Домашнє завдання.

Вивчити означення і властивості перпендикуляра і похилої до площини. Розв’язати задачі:

1. Із точки до площини проведено перпендикуляр завдовжки 9 см і похилу завдовжки 11 см. Знайдіть довжину проекції цієї похилої на площину.

2. Точка, віддалена від вершин правильного трикутника на 5 см, розташована на відстані 4 см від площини трикутника. Знайдіть периметр даного трикутника.

3. Відрізок АВ перетинає площину a в точці О. Проекції відрізків АО і ВО на цю площину дорівнюють 5 см і 20 см відповідно. Знайдіть довжину відрізка АВ, якщо АО=8 см.