Порівняння аксіом шкільної геометрії і аксіом Евкліда
Друкальська Т.С.
Директор Балаклійського ліцею
Балаклійської міської ради
Харківської області
Порівняння аксіом шкільної геометрії і аксіом Евкліда
Математика вимагає точних формулювань та строгих означень. Природа та предмет математичного знання викликали увагу багатьох вчених упродовж віків, починаючи ще з античності. Відомі «Начала» Евкліда, в яких було синтезовано основні результати грецької математичної думки, довгий час були джерелом знань для багатьох наступних поколінь та слугували прикладом строгості математичного викладу. Геометрія досягла великого ступеня логічної досконалості за допомогою аксіоматичного методу Евкліда. Для кращого опанування аксіоматичного методу та його ролі в математики доцільно дослідити розвинення аксіоматики Евкліда та зіставити сучасні формулювання з оригінальними.
В таблиці 1.1 приведено зіставлення аксіом з «Начал» Евкліда з аксіомами, наведеними в підручниках:
Таблиця 1.1
|
Аксіоми Евкліда |
Аксіоми шкільної геометрії |
|
Аксіоми належності |
|
|
Які б не були дві точки |
Через точки Через будь-які дві різні точки можна провести пряму, і тільки одну [5, с. 7]. Через будь-які дві точки можна провести пряму, і до того ж тільки одну [4, с. 7;7, с. 8]. |
Продовження таблиці 2.1
|
На кожній прямій лежить принаймні дві точки. Існує три точки, які не лежать на одній прямій [2, с. 23].
|
Якою б не була пряма, існують точки які належать цій прямій і точки, які не належать їй [3, с. 47; 4, с. 7; 5, с. 7]. |
|
Аксіоми порядку |
|
|
В одному із двох напрямків для кожної точки |
Із трьох точок прямої одна, і тільки одна, лежить між двома іншими [4, с. 8; 5, с. 7; 7, с. 8]. |
|
Аксіома паралельних |
|
|
Через дану точку поза даною прямою можна провести на площині не більше однієї прямої, яка б не перетинала дану [2, с. 50]. |
Через точку, що не лежить на даній прямій, можна провести не більше ніж одну пряму, паралельну даній [7, с. 32]. Через точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній [5, с. 51].
Через точку |
У школі вивчають аксіоми вимірювання та відкладання відрізків і кутів:
Аксіома вимірювання відрізків. Кожен відрізок має певну довжину, що виражається додатним числом у заданих одиницях вимірювання. Довжина відрізка дорівнює сумі довжин частин, на які відрізок ділиться будь-якою точкою [7, с. 16].
Аксіома відкладання відрізків. На будь-якому промені від його початкової точки можна відкласти відрізок заданої довжини, і тільки один [7, с. 16].
Аксіома вимірювання кутів. Кожний кут має градусну міру, що виражається додатним числом. Розгорнутий кут дорівнює ![]() [7, с. 24].
[7, с. 24].
Аксіома відкладання кутів. Від будь-якого променя даної прямої можна відкласти в заданий бік від прямої кут із заданою градусною мірою, меншою за ![]() , і тільки один [7, с. 24].
, і тільки один [7, с. 24].
Евклід же подає це, як теореми:
Теорема для відрізків. Існує, і притому єдина, функція ![]() , визначена на всіх відрізках, яка задовольняє умовам:
, визначена на всіх відрізках, яка задовольняє умовам:
-
Для кожного відрізка
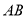
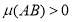 .
.
-
Якщо відрізки
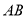 і
і 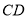 рівні, то
рівні, то 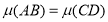 .
.
-
Якщо точка
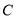 знаходиться між точками
знаходиться між точками 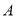 і
і 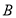 , то
, то 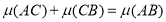 .
.
-
Для деякого відрізка
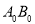
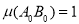 .
.
Число ![]() називається довжиною відрізка, а відрізок
називається довжиною відрізка, а відрізок ![]() – одиницею вимірювання довжини [2, с. 47].
– одиницею вимірювання довжини [2, с. 47].
Теорема для кутів. Існує, і притому єдина, функція ![]() , визначена для всіх кутів, яка задовольняє умовам:
, визначена для всіх кутів, яка задовольняє умовам:
-
Для кожного кута
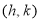
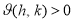 .
.
-
Якщо кути
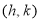 і
і 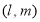 рівні, то
рівні, то 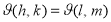 .
.
-
Якщо промінь
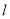 знаходиться між
знаходиться між 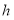 і
і 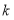 , то
, то 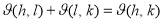 .
.
-
Для деякого кута
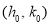 маємо
маємо 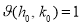 .
.
Число ![]() називається мірою кута, а кут
називається мірою кута, а кут ![]() – одиницею вимірювання кутів [2, с. 47].
– одиницею вимірювання кутів [2, с. 47].
«Начала» й досі залишаються зразком наукової строгості в шкільному викладанні, де користуються дедуктивним методом Евкліда, а не сучасним аксіоматичним методом. Багато теорем, які викладені в сучасних підручниках, за змістом співпадають з тими, які знаходяться в «Началах», методи доведення в багатьох випадках такі ж. Але деякі відмінності все ж існують: в «Началах» взагалі не згадується про вимірювання площі фігур і об’ємів тіл, а також про їх порівняння [1, с. 64].
У Евкліда немає теоремі про те, що площа трикутника дорівнює половині добутку його основи на висоту, а є лише теорема про те, трикутник рівновеликий половині паралелограма з такими ж основою і висотою. Ніде не згадується про число ![]() і його приблизному значенні. Евклід не розраховує довжин, площ і об’ємів, а знаходить за допомогою геометричних побудов відношення між геометричними величинами фігур. Тому і самі слова «довжина», «площа», «об’єм» відсутні в «Началах».
і його приблизному значенні. Евклід не розраховує довжин, площ і об’ємів, а знаходить за допомогою геометричних побудов відношення між геометричними величинами фігур. Тому і самі слова «довжина», «площа», «об’єм» відсутні в «Началах».
З сучасної точки зору найслабшими місцями в «Началах» є спроба визначити основні поняття (точка, пряма, площина) і неповнота аксіоматики [1, с. 64].
В арифметиці Евклід зробив три значних відкриття: сформулював (без доведення) теорему про ділення з остачею; придумав «алгоритм Евкліда» – швидкий спосіб знаходження НСД; першим почав вивчати властивості простих чисел і довів, що їх множина нескінченна.
Знайомство з «Началами» Евкліда корисно кожному математику в наші дні [1, с. 65].
Список використаних джерел:
- Панов В.Ф. Математика древняя и юная. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 648 с.
- А.В. Погорелов. Основания геометрии. – М.; Наука, 1979. 152 с.
- Мерзляк А.Г., Полонський В.Б, Якір М.С. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закладів. – Х.: Гімназія, 2015. – 224 с.
- Істер О.С. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закладів. – К.: Генеза, 2015. – 184 с.
- Бевз Г.П., Бевз В.Г., Владімірова Н.Г. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закладів. – К.: Видавництво «Відродження», 2015. – 192 с.
- Нелін Є.П. Геометрія (профільний рівень): підруч. для 10 кл. закл. загал. серед. освіти – Х.: Видавництво «Ранок», 2018. – 240 с.
- Єршова А.П, Голобородько В.В., Крижановський О.Ф. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закладів. – Х.: Видавництво «Ранок», 2015. 224 с.


про публікацію авторської розробки
Додати розробку
