Порівняння десяткових дробів
Тема: Порівняння десяткових дробів. М-5
Мета: Формування математичних компетентностей учня:
- формувати в учнів поняття порівняння десяткових дробів та правила порівняння десяткових дробів; уміння порівнювати десяткові дроби, використовуючи правила; використовувати правила порівняння десяткових дробів до розв’язання вправ ;
Формування групи компетенцій:
Спілкування рідною / державною мовою: розвивати вміння правильно і чітко висловлювати власні думки; вміння спілкуватися.
Соціальні та громадянські компетентності: готовність до самостійного пошуку розв’язання проблеми, прояву ініціативи, усвідомлення власного внеску в суспільну роботу.
Ініціативність і підприємливість: вміння застосовувати здобуті знання на практиці, розвивати вміння робити висновки.
Уміння вчитися впродовж життя: мати бажання до навчання, розвивати пам'ять, увагу, творчий підхід, бажання організувати власну працю з метою досягнення успішного результату.
Загальнокультурна грамотність: опанувати засади культурного спілкування в ході обговорення завдання.
Інформаційно-цифрова компетентність: вміння використовувати різну інформацію, аналізувати, систематизувати її, розширювати кругозір.
Основні компетентності в природничих науках і технологіях: навчити учнів використовувати здобуті знання з математики під час виконання завдань з інших предметів
Екологічна грамотність і здорове життя: навчити учнів правильно організовувати свою навчальну діяльність і відпочинок.
Очікувані результати:
Після уроку учні зможуть:
- читати і записувати звичайні та десяткові дроби;
Методи, форми і прийоми:
- використання ключових слів;
- Інтерактив « Займи свою позицію»
- інтерактивна гра «Яблунька»
- релаксаційний практикум;
- карусель;
- робота в парах;
- робота в групах;
- самоперевірка;
- взаємоперевірка;
- самодіагностика;
- рефлексія.
Тип уроку: урок - казка
Обладнання: комп’ютер, проектор, екран, картки для практичної роботи.
Хід уроку
І. Організаційний етап.
 Доброго дня, діти! До нас сьогодні завітали гості. Привітаємо ж їх. Але у нас є ще одна гостя
Доброго дня, діти! До нас сьогодні завітали гості. Привітаємо ж їх. Але у нас є ще одна гостя
Тітонька сова- мудра голова,
Хоч вночі літає, все на світі знає.
Різні приклади й задачки
Дуже полюбляє.
Вивчати математику
Всім допомагає.
От вона у вас і перевірить домашнє завдання.

ІІ. Перевірка домашнього завдання.
Яке завдання було вам задано додому?
(№ 1165, 1166)
3 учня йдуть до дошки , решта учнів перевіряють свої роботи.
(На дошці заготовка завдання № 1165)
ІІІ. Актуалізація опорних знань.
Що ж, тітонька Сова говорить, що перш ніж ми почнемо вивчати нову тему, потрібно повторити вже вивчене.
- Яку тему ми розпочали нещодавно вивчати?
(Десяткові дроби)
Завдання 1
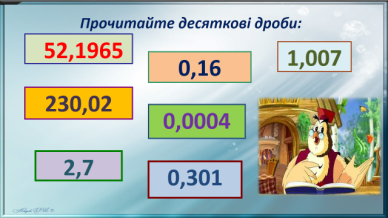
Добре. Але у тітоньки Сови є лісові друзі. І вона просить вас перевірити, чи всі рівності правильні?

Молодці.
ІV. Мотивація навчальної діяльності.
На початку нової теми я хочу запропонувати задачу:.
Задача. Під час проведення змагань з легкої атлетики Богдан стрибнув у висоту на 1,18 м, Микита — на 1,2 м, а Володимир — на 1,09 м. Хто з учнів показав найкращий результат?
- Що потрібно зробити, щоб розв’язати дану задачу?
(Потрібно порівняти числа 1,18; 1,2; 1,09)
- А чи вміємо ми порівнювати десяткові дроби?
(Ні)
- Отже, у нас сьогодні Урок тітоньки Сови: «Порівняння десяткових дробів».
- Пишемо на листках 27 лютого, Класна робота, Порівняння десяткових дробів

 .
.
- Але , щоб відкрити скриньку знань, ми маємо дещо пригадати.

Запитання 1
- Що означає порівняти два числа?
(Порівняти два натуральних числа – означає з’ясувати, яке з них більше, а яке – менше.)
Завдання 2
- Діти, самостійно придумайте два натуральних числа та порівняйте їх. Тільки початку запишіть їх а потім зачитаєте нам.
(Діти по черзі наводять приклади нерівностей)
- Так
Завдання 3
- Сформулюйте правило порівняння звичайних дробів з однаковими знаменниками.
(Із двох звичайних дробів з однаковими знаменниками більший той, у якого чисельник більший; і менший той, у якого чисельник менший.)
Завдання 4
Інтерактив « Займи свою позицію»
- Діти! У вас є листочки. Напишіть на них дріб із знаменником 27. А тепер виходьте всі до дошки та, поспілкувавшись з товаришами, станьте в ряд, починаючи зліва з найменшого звичайного дробу і закінчивши найбільшим дробом справа. Прочитайте нам свої дроби. Молодці! Ви всі добре справилися із завданням.
V. Пояснення нового матеріалу
ПОРІВНЯННЯ ДЕСЯТКОВИХ ДРОБІВ
Щоб навчитися порівнювати десяткові дроби ми виконаємо практичні завдання завдяки яким зможемо вивести правило порівняння десяткових дробів :У вас в завданнях є картки, що пояснюють, як правильно порівнбвати десяткові дроби.
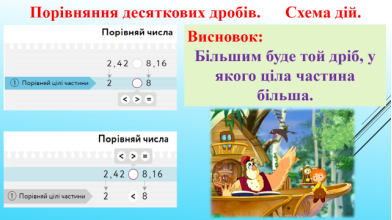
 Випадок 1: Якщо цілі частини десяткових дробів різні.
Випадок 1: Якщо цілі частини десяткових дробів різні.
- Зачитайте, які ми порівнюємо дроби:
- Як ви думаєте, з чого ми почнемо порівняння?
- правильно, з цілих частин.
2 ˂ 8, тому 2,42 ˂ 8,16
 Висновок: Більшим буде той дріб, у якого ціла частина більша.
Висновок: Більшим буде той дріб, у якого ціла частина більша.
Порівняйте дроби:
а) 85,09 і 67,99
б) 256,23 і 25,635
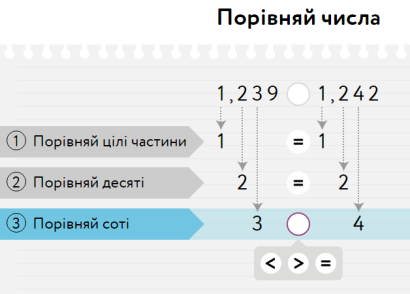
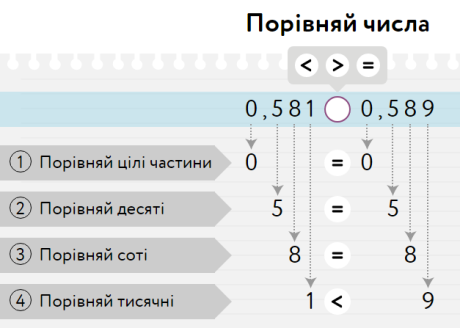
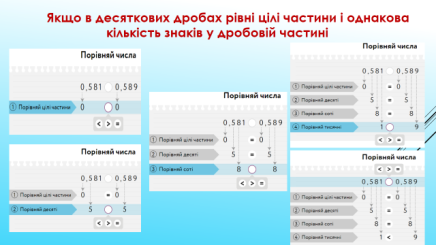 Випадок 2: Якщо в десяткових дробах рівні цілі частини і однакова кількість знаків у дробовій частині
Випадок 2: Якщо в десяткових дробах рівні цілі частини і однакова кількість знаків у дробовій частині
- 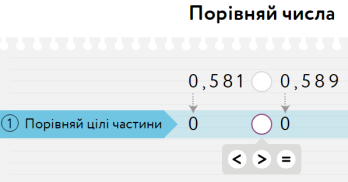 Діти, прочитайте дроби, що порівнюються… (0,581 та 0,589)
Діти, прочитайте дроби, що порівнюються… (0,581 та 0,589)
- Назвіть цілу частину даних лробів… ( Нуль цілих)
- Скільки цифр містить дробова частина?... (три)
- Як називається перший розряд після коми? (десяті)
- Як називається другий розряд після коми? (соті)
-  Як називається третій розряд після коми? (тисячні)
Як називається третій розряд після коми? (тисячні)
- Діти, подивіться уважно, з чого нам пропонують розпочати порівняння? (з десятих)
- Які вони? (5 і 5 )
- Порівняйте їх.
- Якщо вони рівні, то переходимо до порівняння сотих.
-  Назвіть їх. (8 і 8)
Назвіть їх. (8 і 8)
- Порівняйте. ( вони рівні)
- Що робимо далі? (порівнюємо тисячні)
- Назвіть їх. (1і 9)
- Порівняйте числа: (1˂ 9)
- Який зробимо висновок? (0,581 ˂ 0,589)
- У завданнях поставте необхідні знаки нерівності
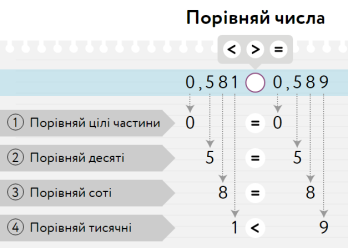

Висновок: Якщо цілі частини десяткових дробів рівні, то порівнюють їх дробові частини порозрядно, починаючи з десятих.
Давайте закріпимо наші знання порівнюючи наступні десяткові дроби.
а) 0,908 і 0,918 б) 7,643 і 7,642
 3) А тепер, перш ніж ми розглянемо порівняння десяткових дробів з однаковою цілою частиною і з різною кількістю цифр у дробовій частині, ми розглянемо…
3) А тепер, перш ніж ми розглянемо порівняння десяткових дробів з однаковою цілою частиною і з різною кількістю цифр у дробовій частині, ми розглянемо…
ВЛАСТИВІСТЬ ДЕСЯТКОВОГО ДРОБУ
Про цю властивість мудра тітонька Сова розповіла своєму учню – Неслуху, а він по секрету розкаже її нам.
Правило 1
Якщо справа до десяткового дробу дописати один або кілька нулів, то отримаємо дріб, що дорівнює даному, наприклад 0,67 = 0,670 = 0,6700 = 0,67000
і т. д. і навпаки, якщо десятковий дріб закінчується нулем або кількома нулями, то ці нулі можна відкинути. Отримаємо дріб, що дорівнює даному, наприклад, 0,800 = 0,80 = 0,8.
Вчитель: - Діти, то як же зміниться десятковий дріб, якщо праворуч приписати один нуль?
 (Дріб залишиться незмінним )
(Дріб залишиться незмінним )
Формування вмінь:
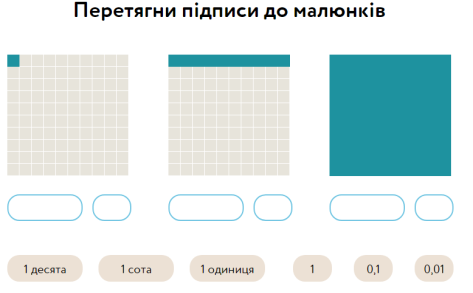
1) Запишіть і назвіть два десяткові дроби, що дорівнюють дробу: а) 0,3; б) 2,46.
1) Спростіть десяткові дроби:
а) 2,500; б) 3,0400; в) 40,0100; г) 9,000.
- Продовжимо, діти, навчатися порівнювати десяткові дроби.
 Алгоритм порівняння десяткових дробів
Алгоритм порівняння десяткових дробів
Щоб порівняти два десяткові дроби з рівними цілими частинами і різною кількістю цифр після коми, потрібно:
1) за допомогою приписування нулів справа зрівняти кількість цифр у дробових частинах;
2) порівняти отримані дробові частини порозрядно, починаючи з десятих.
Наприклад: а) 55,7 і 55,7200;
- У першому дробі ми приписуємо один нуль, а у другому дробі ми відкидаємо два нулі. Отже маємо: 55,70 і 55,72. Чи зможемо ми тепер порівняти наші дроби?
- Порівняйте їх.
- Пригадайте задачу, з якої ми розпочали урок.
 Задача. Під час проведення змагань з легкої атлетики Богдан стрибнув у висоту на 1,18 м, Микита — на 1,2 м, а Володимир — на 1,09 м.
Задача. Під час проведення змагань з легкої атлетики Богдан стрибнув у висоту на 1,18 м, Микита — на 1,2 м, а Володимир — на 1,09 м.
- Чи можемо ми тепер сказати, хто з учнів показав найкращий результат?
1,09 ˂ 1,18 ˂ 1,2
Відповідь: Найкращий результат показав Микита.
 VI. Первинне закріплення матеріалу. Формування вмінь.
VI. Первинне закріплення матеріалу. Формування вмінь.
1. Інтерактивна вправа «Яблунька»:
Діти! Я хочу пперевірити, як ви засвоїли нові правила. У вас на партах є стрілки. Придумайте і запишіть по одному десятковому дробу на кожній картці .
У нас є ще і яблука. Я розмістила їх на «ЯБЛУНЦІ ЗНАНЬ».
1) Щоб поласувати смачними яблуками, які принесуть нам нові знання, потрібно самостійно скласти східці, по яких ви зможете піднятися на деревце. Для цього виходьте до дошки і поспілкувавшись між собою, розмістіть свої дроби на східцях у порядку зростання .
2) Ви дісталися до яблук, але вони всі полетіли вниз. Щоб їх зловити, ви повинні розглянути дроби на картках і прикріпити картки – яблучка з дробами від яблуньки вниз у порядку спадання чисел.
 Час настав для відпочинку – розпочнем
Час настав для відпочинку – розпочнем
Фізкультхвилинку
VII. Вдосконалення вмінь:
Самостійна робота
Розшифруйте імя та прізвище відомого вченого- математика.
1 група
Розмістіть десяткові дроби в порядку зростання:
|
2,23 (И) |
2,03 (С) |
2,3 (М) |
3,2 (Н) |
3,02 (О) |
|
|
|
|
|
|
|
|
|
|
|
|
2 група
Розмістіть десяткові дроби в порядку спадання:
|
7,077 (В) |
7,707 (Т) |
7,77 (С) |
7,7 (Е) |
7,07 (І) |
7 (Н) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Симон Стевін
Історична довідка: Фламандський учений Симон Стевін став відомим насамперед своєю книгою «Десята», виданою фламандською і французькою мовами у 1585 р. Саме після неї в Європі почалося широке використання десяткових дробів. С. Стевін для відокремлення цілої частини від дробової ставив нуль в кружечку. Трактат Стевіна містив практичний опис арифметики десяткових дробів, а також палкий й добре аргументований заклик до їх застосування, зокрема в монетній справі.
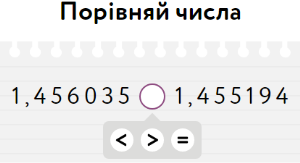
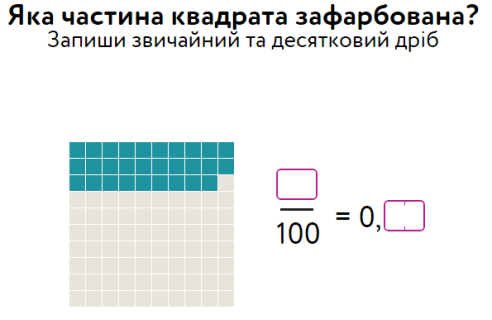
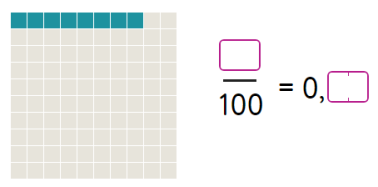
3. Порівняйте десяткові дроби
|
7,305 73,05 |
2,5006 2,0506 |
|
730,5 7305 |
2,0056 2,00560 |
|
0,7305 0,07305 |
2,506 2,50060 |
|
0,0735 0,007305 |
2,5006 2,50060 |
|
73,05 73,050 |
2,56 2,560000 |
|
7,3050 7,30500 |
25,6 25,0600 |
VII. Підсумок уроку.


За допомогою сигнальних карток визначте свій настрій.


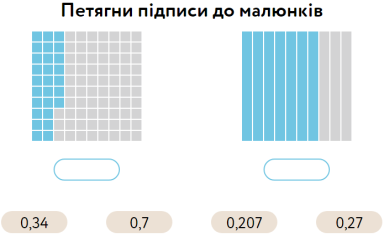

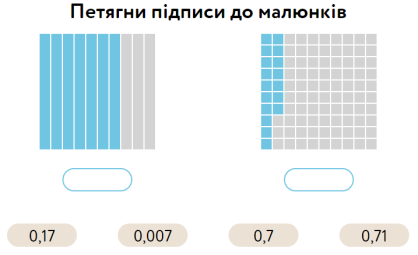

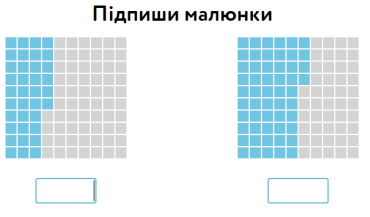
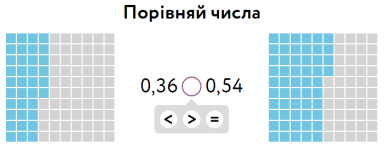
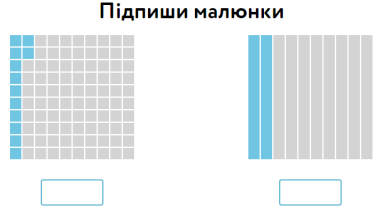
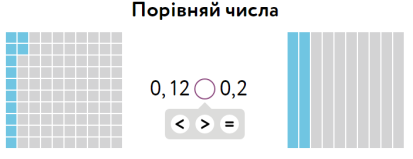
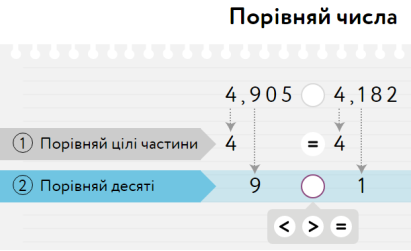
Порівняння дробів. Схема дій.
1. Якщо різні цілі частини


_______________________________________________________________________________________
2. Якщо цілі частини рівні





______________________________________________________________________________________




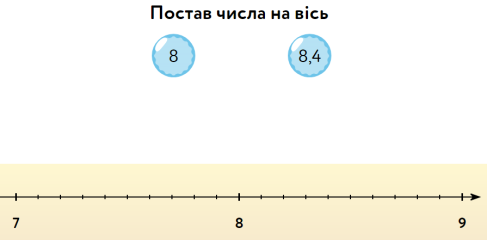
Постав числа на вісь і порівняй їх


______________________________________________________________________________________



____________________________________________________________________________________





![]()
![]()
![]()
![]()
Домашнє завдання
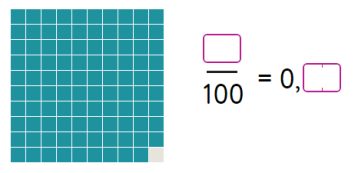



1 мм = ![]() дм
дм








про публікацію авторської розробки
Додати розробку
