Посібник для уроків геометрії І семестр 7 класу (оновлений)
Шановні семикласники!
Ви починаєте вивчати нови й шкільний предмет – геометрію. Це одна з найдавніших наук. Знати геометрію надзвичайно важливо. Це дуже цікавий предмет. Сподіваюся, ви в цьому скоро переконаєтесь. А сприяти вам буде навчальний посібник, який ви тримаєте в руках.
Посібник складається з трьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких проводиться робота з засвоєння понять, термінів і правил блоку навчальної інформації, також наведені вправи і завдання для відпрацювання практичних умінь і навичок.
-
між уроками фронтального опрацювання ви будете виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені

- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен покаже свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Нехай Бог посилає вам мудрості у вивченні геометрії!!!
Тема №1. Елементарні геометричні фігури та їх властивості
Урок №1

Елементарні геометричні фігури та їх властивості
Точка – це перша основа геометрії.
Леонардо да Вінчі
Питання
- Точки і прямі
- Відрізок і його довжина
- Промінь. Кут. Вимірювання кутів
Література
Мерзляк А.Г. та інші Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – Х.: Гімназія, 2015 рік, § 1, пункти 1 – 3, стор. 12 – 36.
Істер О.С. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – К.: Генеза, 2016 рік, § 1 – 3, стор. 6 – 24.
|
1. Точки і прямі |
||
|
1.1 |
Геометрія – це наука про геометричні фігури і їх властивості |
|
|
1.2 |
Планіметрія – це розділ геометрії, в якій вивчаються фігури, які можна розмістити на площині – плоскі. |
|
|
1.3 |
Теорема – це твердження, істинність якого встановлюють за допомогою доведення
Умова Висновок |
|
|
1.4 |
Аксіома – це твердження, яке приймають без доведень |
|
|
1.5 |
Основними фігурами у планіметрії є точка і пряма
|
|
|
1.6 |
Яка б не була пряма, існують точки, що належать цій прямій, і точки, що їй не належать
В
D |
|
|
1.7 |
Основна властивість прямої. Через будь-які дві точки можна провести пряму, і тільки одну |
|
|
1.8 |
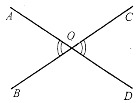
Дві прямі, які мають спільну точку, називають такими, що перетинаються. |
|
|
1.9 |
Теорема. Будь-які дві прямі, що перетинаються, мають тільки одну спільну точку |
|
|
2. Відрізок і його довжина |
||
|
2.10 |
Відрізком АВ називається частина прямої, яка складається з точок А, В та всіх точок, що лежать між ними. Точки А, В називають кінцями відрізка, а всі інші точки – внутрішніми точками. |
|
|
2.11 |
Два відрізки називаються рівними, якщо їх можна сумістити накладанням. |
|
|
2.12 |
Аксіоми вимірювання відрізків |
|
|
|
|
|
||
|
2.13 |
Відстанню між точками А і В називають довжину відрізка АВ. |
|
|
2.14 |
Серединою відрізка АВ називають таку точку |
|
|
3. Промінь. Кут. Вимірювання кутів |
||
|
3.15 |
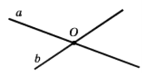
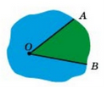
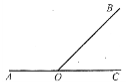
Кожна з частин прямої, утворених при поділі прямої точкою О разом з цією точкою О, називається променем. Точку О називають початком променя. |
|
|
3.16 |
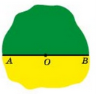
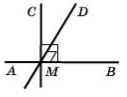
Два промені, які мають спільний початок, називають доповняльними. |
Промені ВС і ВА – доповняльні |
|
3.17 |
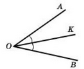
Частину площини, обмежену двома променями зі спільним початком, називають кутом. |
ОА, АВ – сторони кута, О – вершина кута ОК – бісектриса |
|
3.18 |
Промені, що обмежують кут, називають сторонами, а їх спільний початок – вершиною кута |
|
|
3.19 |
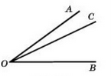
Внутрішній промінь, який розбиває кут на два рівні кути, називається бісектрисою кута |
|
|
3.20 |
Кут, сторони якого – доповняльні промені, називається розгорнутим |
|
|
3.21 |
Аксіоми вимірювання кутів |
|
Розгорнутий – 180°; Прямий – 90°; Гострий – менше 90°; Тупий – більше 90° |
||
|
|
|
Урок №2
«Своє серце зверни до навчання,
а свої уші – до розумних речей.»
Книга приповістей Соломонових 23:12
Фронтальне опрацювання матеріалу
Властивості точок і прямих
І. Робота над засвоєнням понять, термінів і правил
Завдання 1
- Повтори тези 1.1 – 1.9 блоку № 1.
- Усно дай відповідь на питання:
- Що таке геометрія?
- Які фігури називаються плоскими?
- Що таке планіметрія?
- Що називають теоремою?
- Що називають аксіомою?
- Які фігури є основними у планіметрії?
- Як розміщуються точки і прямі на площині?
- Сформулюй основну властивість прямої.
- Дай означення прямих, які перетинаються.
- Сформулюй теорему про прямі, які перетинаються.
-
 Як розміщуються три точки на прямій?
Як розміщуються три точки на прямій?
Завдання 2
Усно виконай вправи:
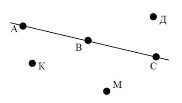
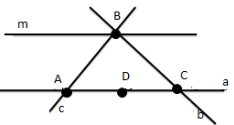
2.1. Розглянь рис.1 і дай відповіді на запитання:
- На яких прямих лежать точки А, В, С і D?
- Які прямі проходять через точку А, В, С і D? Рис.1
- В якій точці перетинаються прямі а і b, b i c, c i m, b i m?
-
У якій точці перетинаються три прямі? Назвіть ці прямі.
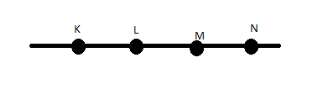
- Точка М лежить між точками К і N. Як розміщені точки М і N відносно точки К?
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи:
- Познач у зошиті точки А і В та проведи через них пряму. Назви цю пряму.
- Пряма АВ перетинає пряму АС у точці А, а пряму ВС у точці В. Чи належить точка С прямій АВ?
-
Пряма a і точки А, В такі, що
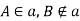 . Зобрази це на малюнку.
. Зобрази це на малюнку.
Завдання 4
Письмово виконай вправи з підручника геометрії за авторством Істера О.С., стор. 10 – 11: 8; 9; 10.
Урок №3
«Бо для Бога нема неможливої жодної речі»
Євангеліє від Луки 1:37
Фронтальне опрацювання матеріалу
Відрізок і його довжина
І. Робота над засвоєнням понять, термінів і правил
Завдання 1
- Повторити тези 2.10 – 2.14 блоку № 1.
- Усно дати відповідь на питання:
- Що називають відрізком?
- Що називають кінцями відрізка?
- Які два відрізки називаються рівними?
- Сформулюйте аксіоми вимірювання відрізків.
- Що називають відстанню між двома точками?
-
Яку точку називають серединою відрізка АВ?
- Виконайте усно вправу 26 на ст. 21.
- Пригадайте основні відомості про відрізки (презентація вчителя).
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 2.
Виконайте письмово вправи на стор. 21 – 23:
20, 30, 34 (2), 39.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних вправ
Завдання 3.
Виконайте вправу 46 на ст. 24.
Уроки №4, 5
«Гординя людини її понижає,
а честі набуває покірливий духом»
Книга приповістей Соломонових 29:23
Фронтальне опрацювання матеріалу
Промінь. Кут. Вимірювання кутів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.12 – 3.16 блоку №1.
- Усно дати відповідь на питання:
- Що називають кутом?
- Що називають сторонами, вершиною, бісектрисою кута?
- Який кут називається розгорнутим?
- Сформулювати аксіоми вимірювання кутів.
- У яких одиницях вимірюють кути?
- Яка градусна міра розгорнутого кута?
- Що називають променем?
- Які два промені називають доповняльними?
Завдання 2.
- Усно пригадайте основну інформацію про кути, яку ви вивчили у 5 класі (презентація вчителя).
- Усно виконати вправи з підручника (стор. 32): 54, 56.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Письмово виконати вправи на стор. 33 – 35:
Завдання 2.
63, 65, 70, 75.
Завдання 3.
Виконайте практичну роботу
«Найпростіші геометричні фігури і їх властивості»
Завдання 1. Накресліть відрізок завдовжки 6 см. Візьміть на відрізку довільну точку, знайдіть довжини утворених відрізків. Як перевірити, чи правильно проведене вимірювання?
Завдання 2. Точка D належить відрізку АС. Знайдіть відстань між точками А і С, якщо АD=5,3 см; СD=4,9 см.
Завдання 3. Точка К належить відрізку МN. Довжина відрізка МК дорівнює 5,2 см, а відрізок КN на 1,1 см коротший від відрізка МК. Чому дорівнює довжина відрізка МN

Завдання 4. Точки А, В, С лежать на одній прямій. Відомо, що АВ=4,7см; АС=2,1 см; ВС=6,8 см.
- Чи може точка С лежати між точками А і В?
- Чи може точка В лежати між точками А і С?
Завдання 5. На відрізку МN завдовжки 12 см взято точку К. Знайдіть довжини відрізків МК і КN, якщо:
- відрізок МК на 3 см довший від відрізка КN;
- відрізок МК у 3 рази довший від відрізка КN.
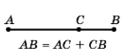
Завдання 6. На прямій АВ відмітьте точку С так, щоб точка В лежала між точками А і С. Назвіть утворені відрізки, промені. Що можна сказати про промені АВ і АС, ВА і ВС?
![]()
Завдання 7. На прямій а відмічена точка В. Відкладіть від точки В на прямій а відрізок довжиною 3,5 см. Скільки можна відкласти таких відрізків?
![]()
Завдання 8. Накресліть кут 110°. Проведіть промінь між сторонами цього кута. Виміряйте утворені кути. Як ви переконаєтесь, що вимірювання виконане правильно?
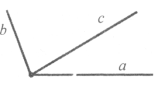
Завдання 9. Чи можуть точки А, В, С лежати на одній прямій, якщо АВ=1,8 м, АС=1,3 м, ВС=3 м? Поясніть відповідь.
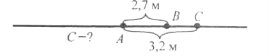
Завдання 10. Точки А, В, С лежать на одній прямій. Знайдіть довжину відрізка ВС, якщо АВ=2,7 м, АС=3,2 м. Скільки розв’язків має задача?
![]()
Завдання 11. Відстань між точками А і В дорівнює 5 см. Знайдіть на прямій АВ такі точки, для кожної з яких сума відстаней до точок А і В дорівнює 9 см.
Завдання 12. В одному ряду фруктового саду через кожні 7,8 м посаджені яблуні, всього 27 яблунь; між кожними двома сусідніми яблунями посаджено кущ смородини. Визначити відстань від крайнього в ряді куща смородини:
- до крайніх у цьому ряді яблунь;
- до середньої яблуні;
- до другого від краю куща смородини;
- до двох середніх кущів смородини.

Готуємось до індивідуального опрацювання матеріалу
- Точки К, М і N лежать на одній прямій. KM=3 см, MN=10 см. Знайдіть KN. Розгляньте два випадки.
- На прямій послідовно позначено точки А, В, С і D. АС =4 см, ВD=3 см, ВС=1,5 см. Знайдіть АD.
-
Промінь ОС ділить
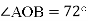 на два кути так, що один з них у 7 рази більший за другий. Знайдіть
на два кути так, що один з них у 7 рази більший за другий. Знайдіть 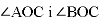 .
.
Урок №7
Ніхто більшої любови не має над ту,
як хто свою душу поклав би за друзів своїх
Євангеліє від Івана 15:13
Внутрішньопредметне узагальнення матеріалу
Елементарні геометричні фігури та їх властивості
І. Засвоєння термінології до теми
Завдання 1.
- Повторити блок № 1.
- Письмово дати відповідь на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
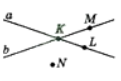 Усно виконати вправи:
Усно виконати вправи:
-
Яка із точок на малюнку не належить ані прямій
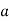 , ані прямій
, ані прямій 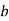 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Укажіть, який із кутів є тупим?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
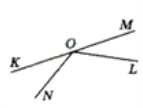 За даним малюнком укажіть пару доповняльних променів:
За даним малюнком укажіть пару доповняльних променів:
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
-
Накреслити відрізки
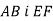 такі, що
такі, що 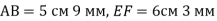 . Порівняти довжини відрізків
. Порівняти довжини відрізків 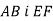 .
.
-
Накресліть кут, градусна міра якого дорівнює
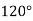 і проведіть його бісектрису.
і проведіть його бісектрису.
-
Промінь
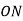 ділить кут АОВ на два кути. Знайдіть кут
ділить кут АОВ на два кути. Знайдіть кут 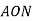 , якщо
, якщо 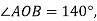
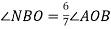 .
.
-
Точки
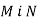 належать відрізку АВ, довжина якого дорівнює 40 см. Знайдіть довжину відрізка
належать відрізку АВ, довжина якого дорівнює 40 см. Знайдіть довжину відрізка 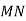 , якщо
, якщо 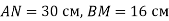 .
.
-
Відрізок
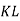 , довжина якого 11,6 см, поділено на три частини. Довжина однієї з них на 2,4см менша за довжину другої і вдвічі менша за довжину третьої. Знайдіть довжину меншої з цих сторін.
, довжина якого 11,6 см, поділено на три частини. Довжина однієї з них на 2,4см менша за довжину другої і вдвічі менша за довжину третьої. Знайдіть довжину меншої з цих сторін.
Тема №2. Взаємне розміщення прямих на площині
Урок №1

Взаємне розміщення прямих на площині
«Невдача - це просто можливість
почати знову, але вже більш мудро»
Генрі Форд
Питання
- Суміжні і вертикальні кути.
- Перпендикулярні прямі.
- Паралельні прямі.
Література
Мерзляк А.Г. та інші Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – Х.: Гімназія, 2015 рік, § 1, пункти 4 – 6, стор. 36 – 54; § 3, пункти 13 – 15, стор. 104 – 123.
Істер О.С. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – К.: Генеза, 2016 рік, § 4 – 10, стор. 25 – 69.
|
1. Суміжні і вертикальні кути |
||
|
1.1 |
Два кути називають суміжними, якщо в них одна сторона спільна, а дві інші є доповняльними променями. |
|
|
1.2 |
Теорема. Сума суміжних кутів дорівнює 180° |
|
|
1.3 |
Два кути називають вертикальними, якщо сторони одного кута є доповняльними променями сторін другого |
|
|
1.4 |
Теорема. Вертикальні кути рівні |
|
|
2. Перпендикулярні прямі |
||
|
2.5 |
Дві прямі називаються перпендикулярними, якщо при їхньому перетині утворився прямий кут.
|
|
|
2.6 |
Два відрізки називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих. |
|
|
2.7 |
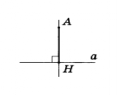
Відрізок, перпендикулярний до прямої, один кінець якого лежить на цій прямій, називають перпендикуляром, опущеним з точки на пряму. |
|
|
2.8 |
Довжину перпендикуляра називають відстанню від точки до прямої. |
|
|
2.9 |
Через кожну точку прямої проходить лише одна пряма, перпендикулярна до даної. |
|
|
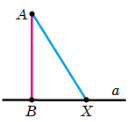
2.10 |
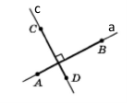
Будь-який відрізок, проведений з точки до прямої, відмінний від перпендикуляра, називається похилою. АВ – перпендикуляр; В – основа перпендикуляра АХ – похила; Х – основа похилої |
|
|
3. Паралельні прямі |
||
|
3.11 |
Дві прямі називаються паралельними, якщо вони не перетинаються
|
|
|
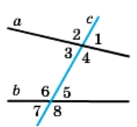
3.12 |
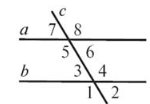
Пряма, яка перетинає дві інші прямі, називається їх січною. З двома даними прямими вона утворює 8 кутів, деякі пари яких мають окремі назви: 3 і 5, 4 і 6 – внутрішні різносторонні; 3 і 6, 4 і 5 – внутрішні односторонні; 2 і 6, 1 і 5, 3 і 7, 4 і 8 – відповідні; 2 і 8, 1 і 7 – зовнішні різносторонні; 2 і 7, 1 і 8 – зовнішні односторонні. |
|
|
3.13 |
Ознаки паралельності прямих: |
|
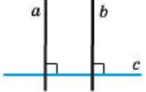
|
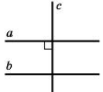
1) Дві прямі, які перпендикулярні до третьої прямої, паралельні.
|
|
|
|
2) Якщо різносторонні кути, утворені при перетині двох прямих січною, рівні, то прямі паралельні. |
|
|
|
3) Якщо сума односторонніх кутів, утворені при перетині двох прямих січною, дорівнює 180º, то прямі паралельні. |
||
|
4) Якщо відповідні кути, утворені при перетині двох прямих січною, рівні, то прямі паралельні |
||
|
3.14 |
Аксіома паралельності прямих Через точку, яка не лежить на даній прямій, проходить тільки одна пряма, паралельна даній. |
|
|
3.15 |
Властивості паралельних прямих: |
|
|
1) Якщо дві паралельні прямі перетинаються січною, то різносторонні кути рівні. |
|
|
|
2) Якщо дві паралельні прямі перетинаються січною, то сума односторонніх кутів дорівнює 180º. |
||
|
3) Якщо дві паралельні прямі перетинаються січною, то відповідні кути рівні. |
||
|
4) Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.
|
|
|
|
5) Якщо дві прямі паралельні третій прямій, то вони паралельні. |
||
|
3.16 |
Відстанню між двома паралельними прямими називають відстань від будь-якої точки однієї з прямих до другої прямої. |
|
Уроки №2, 3
«…з усіх втрат втрата часу найтяжча...»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Суміжні кути та їх властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.2 боку № 2.
- Усно дати відповідь на питання:
- Що таке геометрія?
- Які фігури називаються плоскими?
- Що таке планіметрія?
- Які фігури є основними у планіметрії?
- Що називають променем? відрізком?
- Які промені називаються доповняльними?
- Що називають кутом?
- Який кут називається розгорнутим?
- Які кути називаються суміжними?
- Яку властивість мають суміжні кути?
Завдання 2.
Усно виконати вправи з підручника (стор. 38): 88, 91, 92, 93, 94.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Письмово виконати вправи з підручника (стор. 38 – 41):
Завдання 3.
86, 98, 107, 108.
Завдання 4.
Виконати вправи за готовими малюнками:
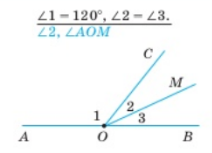
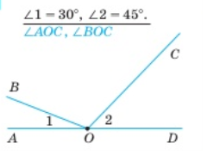
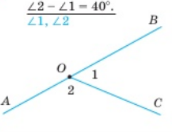
Завдання 5.
- Різниця між двома суміжними кутами дорівнює меншому з них. Знайдіть ці кути.
- Знайдіть кут, якщо сума двох кутів, суміжних з ним, дорівнює 240°.
- Різниця двох суміжних кутів відноситься до одного з них як 5 : 2. Знайдіть ці суміжні кути.
- Бісектриса кута утворює з променем, доповняльним до сторони даного кута, кут 130°. Знайдіть даний кут.
Урок №4
«Блаженна людина, що мудрість
знайшла, і людина, що розум одержала»
Книга приповістей Соломонових 3:13
Фронтальне опрацювання матеріалу
Вертикальні кути та їх властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.4 блоку № 2.
- Усно відповісти на питання:
- Які кути називаються суміжними?
- Сформулювати властивість суміжних кутів.
- Які кути називаються вертикальними?
- Сформулювати властивість вертикальних кутів.
Завдання 2.
Усно виконати вправи (стор. 38): 89, 96.
ІІ. Відпрацювання практичних умінь та навичок
Письмово виконати вправи з підручника (стор. 40):
Завдання 3.
101 (1), 104.
Завдання 4.
Накресліть прямі а і b, що перетинаються в точці О під кутом 80°.
- Позначте однаковим кольором усі пари вертикальних кутів, що утворилися на рисунку. Якими є градусні міри цих кутів?
-
Проведіть через точку О пряму
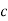 , що утворює з прямою а прямий кут. Чи буде пряма с утворювати прямий кут з прямою b?
, що утворює з прямою а прямий кут. Чи буде пряма с утворювати прямий кут з прямою b?
Завдання 5.
Накресліть таблицю в зошиті та заповніть її.
|
Даний кут |
Суміжний з ним кут |
Вертикальний йому кут |
|
60˚ |
|
|
|
170˚ |
|
|
|
10˚ |
|
|
|
90˚ |
|
|
|
50˚ |
|
|
|
120˚ |
|
|

Готуємось до індивідуального опрацювання матеріалу
- Один із суміжних кутів в 11 разів менший від другого. Знайдіть ці кути.
- Знайдіть суміжні кути, якщо їхні градусні міри відносяться як 9:11.
-
Сума двох кутів, які утворилися при перетині двох прямих, дорівнює
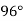 . Знайдіть кожний з кутів, утворений при перетині цих прямих.
. Знайдіть кожний з кутів, утворений при перетині цих прямих.
- Один з чотирьох кутів, що утворилися при перетині двох прямих, у 4 рази більший за суму суміжних з ним кутів. Знайдіть ці чотири кути.
Урок №6
«І пізнаєте правду, а правда
вас вільними зробить!»
Євангелія від Івана 8:32
Фронтальне опрацювання матеріалу
Перпендикулярні прямі. Перпендикуляр
І. Робота над засвоєнням понять, термінів і правил
 Завдання 1.
Завдання 1.
- Повторити тези 2.5 – 2.9 блоку № 2.
- Усно дайте відповіді на питання:
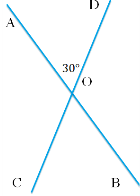
- Що зображено на малюнку?
- Назвіть вертикальні кути зображені на малюнку.
- Яку властивість вертикальних кутів ви пам’ятаєте?
- Назвіть суміжні кути, зображені на малюнку.
- Сформулюйте властивість суміжних кутів.
- Знайдіть всі інші кути, якщо ∠AOD=30°.
- Сформулюйте означення перпендикулярних прямих.
- Що називають перпендикуляром? Відстанню від точки до прямої?
- Які види кутів ви знаєте? Якими можуть бути їх градусні міри?
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 2.
-
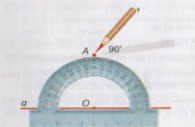 Складіть алгоритм побудови перпендикулярної прямої до даної прямої через дану точку за допомогою косинця. Виконайте дану побудову в зошиті.
Складіть алгоритм побудови перпендикулярної прямої до даної прямої через дану точку за допомогою косинця. Виконайте дану побудову в зошиті.
- Складіть алгоритм побудови перпендикулярної прямої до дано прямої через дану точку за допомогою транспортира та лінійки. Виконайте дану побудову в зошиті.
Завдання 3.
-
Прямі АВ і СD є перпендикулярними і перетинаються в точці О. Промінь ОЕ проходить між променями ОА і ОD, а промінь OF проходить між променями ОВ і ОС,
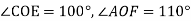 . Знайдіть кут EOF.
. Знайдіть кут EOF.
-
 Прямі
Прямі 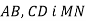 перетинаються в точці О, причому
перетинаються в точці О, причому 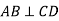 . Знайдіть
. Знайдіть 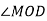 , якщо
, якщо 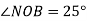 .
.
- Сума двох кутів, утворених при перетині двох прямих, у п’ять разів більша за суму двох інших. Знайти градусні міри всіх утворених кутів.
Урок №7
«Поводься так, ніби ти вже щасливий,
і ти дійсно станеш щасливішим»
Дейл Карнегі
Фронтальне опрацювання матеріалу
Перпендикулярні прямі та їх властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 2.5 – 2.9 блоку № 2.
- Усно відповісти на питання:
- Які дві прямі називають перпендикулярними?
- Яким символом позначають перпендикулярні прямі?
- Які два відрізки називають перпендикулярними?
- Що називають відстанню від точки до прямої?
-
Скільки через кожну точку прямої можна провести прямих, перпендикулярних до даної?
-
Яке із слів: пряма, промінь чи відрізок, можна поставити замість крапок, щоб утворились правильне твердження: існує …, що проходить паралельно прямій
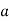 і:
і:
-
Яке із слів: пряма, промінь чи відрізок, можна поставити замість крапок, щоб утворились правильне твердження: існує …, що проходить паралельно прямій
-
Перетинає тільки пряму
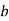 ;
;
-
Перетинає тільки пряму
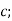
-
Не перетинає ні прямої
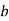 , ні прямої
, ні прямої 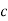 ;
;
-
Перетинає і пряму
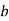 , і пряму
, і пряму 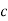 .
.
- Вправи за готовими рисунками:
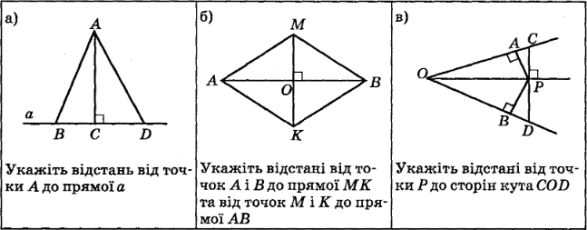
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 2.
Письмово виконайте вправи з підручника (стор. 45 – 46)
117, 123.
Завдання 3.
Пряма ![]() перпендикулярна до відрізка АВ, довжина якого 9 см, і проходить через точку С, яка належить цьому відрізку і ділить його у відношенні 8:10, починаючи з точки А. Знайдіть відстані від точок А і В до прямої
перпендикулярна до відрізка АВ, довжина якого 9 см, і проходить через точку С, яка належить цьому відрізку і ділить його у відношенні 8:10, починаючи з точки А. Знайдіть відстані від точок А і В до прямої ![]() .
.
Урок №8
«Джерело скаламучене чи зіпсутий потік –
це справедливий, що схиляється перед безбожним»
Книга приповістей Соломонових 25:26
Фронтальне опрацювання матеріалу
Паралельні прямі. Аксіома паралельних прямих
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 3.11, 3.14, 3.16 блоку № 2.
- Усно встав пропущені слова:
- Дві прямі називаються паралельними, якщо вони …
- Дві прямі називаються перпендикулярними, якщо …
- Аксіома паралельних прямих: через точку, яка … на даній прямій, можна провести …, паралельну даній.
- Відстанню між двома паралельними прямими називають …
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Вкажи паралельні прямі на малюнку, запропонованому вчителем.
- Вкажи перпендикулярні прямі на малюнку, запропонованому вчителем.
- Вкажи паралельні та перпендикулярні прямі на малюнку, запропонованому вчителем.
Завдання 4.
Письмово виконай вправи, стор. 107, 108 підручника: 285, 286, 297.
ІІІ. Відпрацювання навиків розв’язування нестандартних вправ
Завдання 5.
- Усно виконай вправу з рубрики «Це цікаво», запропоновану вчителем.
- Усно виконай вправу 299, стор. 108 підручника.
Урок №9
«Тим, хто любить Бога, хто покликаний
Його постановою, усе допомагає на добре»
Послання до римлян 8:28
Фронтальне опрацювання матеріалу
Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 3.11 – 3.14 блоку № 2.
- Усно дай відповідь на питання:
- Як можуть розміщуватись прямі на площині?
- Як називаються прямі на площині, які не перетинаються?
-
 Що допомагає нам з’ясувати чи паралельні прямі чи ні?
Що допомагає нам з’ясувати чи паралельні прямі чи ні?
- Як називається пряма, яка перетинає дві інші прямі?
- Яким приладом вимірюють кути?
- Як називаються кути 1 і 5; 2 і 6; 3 і 7; 4 і 8?
- Яку назву мають кути 3 і 6; 4 і 5?
- Як називаються кути 3 і 5; 4 і 6?
- Сформулюй ознаки паралельних прямих.
- Сформулюй аксіому паралельності прямих.
Завдання 2.
Виконай практичне завдання:
-
Проведи довільну пряму
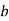 .
.
-
Постав точку
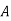 , яка не належить прямій
, яка не належить прямій 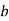 .
.
-
За допомогою косинця та лінійки побудуй пряму
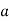 , паралельну прямій
, паралельну прямій 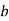 , яка проходить через точку
, яка проходить через точку  .
.
- Проведи січну.
- Познач:
- внутрішні різносторонні кути цифрами 1 і 2;
- внутрішні односторонні кути – 1 і 3;
- відповідні – 4 і 3.
- Виміряй їх величину за допомогою транспортира.
- Запиши результати вимірів у зошит.
- Зроби висновок для кожного випадку, порівнявши величини кутів.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Письмово виконай вправи, стор. 48 – 49 підручника за авторством Істера О.С.: 171; 175; 179.
- Січна перетинає дві дані прямі; при цьому утворилися внутрішні односторонні кути, різниця яких дорівнює 108°, а відношення – 4 : 1. Доведіть, що дані прямі паралельні.
Урок №10
«Шукайте ж найперш царства Божого
й правди Його…»
Євангелія від Матвія 6:33
Фронтальне опрацювання матеріалу
Ознаки паралельності прямих
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
Повторити тези 2.10 – 2.13 блоку № 2.
 Завдання 2.
Завдання 2.
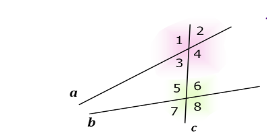
- Дивлячись на малюнок, назвіть внутрішні односторонні кути.
- Дивлячись на малюнок, назвіть відповідні кути.
- Дивлячись на малюнок, назвіть внутрішні різносторонні кути.
- Дві прямі, які лежать в одній площині і ніколи не перетинаються, називають ...
-
Один із суміжних кутів дорівнює
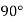 . Яка градусна міра другого?
. Яка градусна міра другого?
- Чи може одна із суміжних кутів бути розгорнутим?
-
Один з вертикальних кутів дорівнює
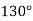 . Знайти другий вертикальний кут.
. Знайти другий вертикальний кут.
- За якої умови сума градусних мір вертикальних кутів дорівнює 180 градусів?
- Як називається твердження, яке не потребує доведення?
- Як називається пряма, яка перетинає дві інші прямі?
- Як називаються прямі, які при перетині утворюють прямий кут?
-
Чому дорівнює градусна міра вертикальних кутів, якщо сума їх градусних мір дорівнює
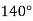 ?
?
- Сформулюйте ознаки паралельності прямих.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Усно виконати вправи, запропоновані вчителем у презентації.
Завдання 4.
-
 Письмово виконати вправи за готовими малюнками, запропоновані вчителем у презентації.
Письмово виконати вправи за готовими малюнками, запропоновані вчителем у презентації.
- За бажанням вдома виконати тестування, яке зашифроване у QR-коді:
Уроки №11, 12
«Щоб дійти до мети, треба перш за все йти»
Оноре де Бальзак
Фронтальне опрацювання матеріалу
Властивості паралельних прямих. Властивості кутів, утворених при перетині двох паралельних прямих січною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 2.10 – 2.14 блоку № 2.
- Усно відповісти на питання:
- Які прямі називаються паралельними?
- Яка пряма називається січною?
- Скільки кутів утворюється при перетині двох прямих січною? Як вони називаються?
- Сформулювати ознаки паралельності прямих.
- Як читається аксіома паралельних прямих?
-
Сформулювати властивості паралельних прямих.
- Усно виконати вправи 326 стор. 120 підручника.
- Задачі за готовими рисунками:
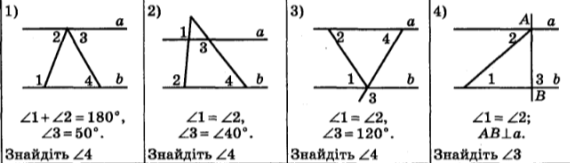
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Письмово виконати вправи з підручника, стор. 120 – 122:
Завдання 2.
328, 330 (2), 341.
Завдання 3.
Виконайте кросворд «Взаємне розміщення прямих»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- Прямі, які при перетині утворюють прямі кути .
- Положення двох прямих , які мають одну спільну точку.
- Кути, які знаходяться між прямими по один бік від січної.
- Кути, які утворюються при заміні одного з внутрішніх різносторонніх кутів на вертикальний кут.
- Прямі, які не перетинаються .
- Пряма, що перетинає дві паралельні прямі одночасно.
- Довжина відрізка, що сполучає дві точки.
- Рівні кути, що утворюються при перетині двох прямих.
- Креслярський прилад.
- Кут, який дорівнює 180 градусів.
- Фігури, розміщені на площині.
- Кути, які утворюються перпендикулярними прямими.
- Прилад для вимірювання величини кутів.
Завдання 4.
- Виконайте інтеративне тестування, яке знаходиться за посиланням https://learningapps.org/view3755782
-
За перетину двох паралельних прямих січною утворилося 8 кутів. Сума трьох із них дорівнює
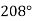 . Знайдіть величину кожного з цих восьми кутів.
. Знайдіть величину кожного з цих восьми кутів.
-
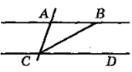 На рисунку
На рисунку 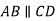 ,
, 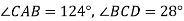 . Доведіть, що СВ – бісектриса кута ACD.
. Доведіть, що СВ – бісектриса кута ACD.

Готуємось до індивідуального опрацювання матеріалу
-
Один з восьми кутів, що утворились при перетині двох паралельних прямих січною, дорівнює 1) 46°; 2)
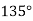 . Знайдіть решту кутів.
. Знайдіть решту кутів.
- Сума двох із восьми кутів, які утворились при перетині двох паралельних прямих січною, дорівнює 68°. Знайдіть кожний з восьми кутів.
-
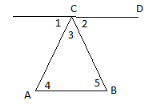
На рисунку
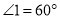 ,
, 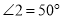 і АВ паралельна CD. Знайдіть міри кутів 3, 4 і 5.
і АВ паралельна CD. Знайдіть міри кутів 3, 4 і 5.
Урок №14
«Я все можу в Тім, Хто мене
підкріпляє, в Ісусі Христі»
Послання до филип’ян 4:13
Внутрішньопредметне узагальнення матеріалу
Взаємне розміщення прямих на площині
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторіть блок № 2.
- Дайте письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2
Усно виконати вправи:
- Укажіть пару кутів, які можуть бути суміжними?
|
А |
Б |
В |
Г |
|
|
|
|
|
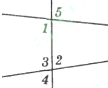
- Укажіть який з кутів є внутрішнім різностороннім з кутом 1.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
- Знайдіть величину кожного з кутів, які утворюються при перетині двох прямих, якщо сума двох з них дорівнює 84°.
-
Один із кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює
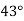 . Знайдіть решту кутів.
. Знайдіть решту кутів.
-
Через вершину D трикутника DEF проведено пряму, паралельну стороні EF. Знайдіть кут EDF, якщо
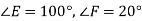 .
.
-
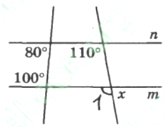 За даним малюнком знайдіть градусну міру кута
За даним малюнком знайдіть градусну міру кута 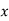 .
.
Тема №3. Трикутники. Ознаки рівності трикутників
Урок №1

Трикутники. Ознаки рівності трикутників
Геометрія – це інтуїція
Г. Гельмгольц
Питання
- Трикутник і його елементи.
- Ознаки рівності трикутників.
Література
Мерзляк А.Г. та інші Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – Х.: Гімназія, 2015 рік, § 2, пункти 7, 8, стор. 55 – 74, пункти 11, 12, стор. 87 – 97, § 3, пункт 16, стор. 124 – 133.
Істер О.С. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – К.: Генеза, 2016 рік, § 11 – 18, стор. 70 – 107.
|
||
|
1.1 |
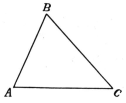
Фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки, називають трикутником.
|
А, В, С – вершини АВ, ВС, АС – сторони
Р = АВ + ВС + АС |
|
1.2 |
Суму довжин усіх сторін трикутника називають його периметром. |
|
|
1.3 |
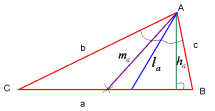
Відрізок, що сполучає вершину трикутника із серединою його протилежної сторони, називають медіаною трикутника. |
|
|
1.4 |
Відрізок бісектриси кута трикутника, який сполучає вершину трикутника з точкою протилежною сторони, називають бісектрисою трикутника. |
|
|
1.5 |
Перпендикуляр, опущений з вершини трикутника на пряму, яка містить протилежну сторону, називають висотою трикутника. |
|
|
1.6 |
Зовнішнім кутом трикутника називають кут, суміжний із кутом цього трикутника. |
|
|
1.7 |
Теорема. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним. |
|
|
1.8 |
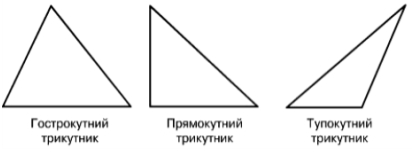
Види трикутників за кутами: 1) прямокутний – трикутник, який має один прямий кут; 2) тупокутний – трикутник, який має один тупий кут; 3) гострокутний – трикутник, у якого всі кути гострі.
|
|
|
1.9 |
Теорема. Сума кутів трикутника дорівнює 180º. |
|
|
||
|
2.10 |
Фігури, які можна сумістити накладанням, називають рівними. |
|
|
2.11 |
Якщо кожна з двох фігур дорівнює третій, то перша і друга фігури також рівні.
|
1 2 3 |
|
2.12 |
Якщо трикутники рівні, то рівні їх відповідні сторони та кути. |
|
|
2.13 |
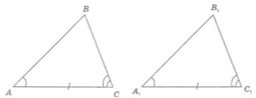
Теорема (1 ознака рівності трикутників) Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. |
За двома сторонами і кутом між ними |
|
2.14 |
Теорема (2 ознака рівності трикутників) Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні. |
За стороною і двома прилеглими кутами |
|
2.15 |
Теорема (3 ознака рівності трикутників) Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні. |
За трьома сторонами
|
Урок №2
«Хто стоїть на місці, той відстає»
Давньоримське прислів'я
Фронтальне опрацювання матеріалу
Трикутник та його елементи
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.6, 1.8 блоку № 3.
- Усно дати відповідь на питання:
- Що називають трикутником?
- Чому дорівнює периметр трикутника?
- Що називають медіаною трикутника?
- Що називають бісектрисою трикутника?
- Що називають висотою трикутника?
- Які є види трикутників за кутами?
Завдання 2.
Усно виконати вправи, стор. 72 підручника за редакцією О.С. Істера: 264; 265.
ІІ. Відпрацювання умінь та навичок розв’язування вправ
Завдання 3.
- Письмово виконати вправи стор. 72 підручника за редакцією О.С. Істера: 266.
- За малюнком запишіть умову та розв’яжіть задачу.

Завдання 4.
4.1. Письмово виконати вправи стор. 72 – 73 підручника за редакцією О.С. Істера: 276.
4.2. Виконайте інтерактивну вправу, розміщену за посиланням
https://learningapps.org/display?v=puy16wnqn16
ІІІ. Відпрацювання умінь та навичок розв’язування нестандартних вправ
Завдання 5.
У трикутнику АВС сторони АВ і ВС рівні, ВD – медіана. Периметр трикутника АВD дорівнює 21 см, а периметр трикутника СВD – 18 см. Знайдіть периметр трикутника АВС, якщо ВD = 7 см.
Урок №3
«Бджола мала, а й та працює»
Українське прислів’я
Фронтальне опрацювання матеріалу
Зовнішній кут трикутника
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.8 блоку № 3.
- Усно відповісти на питання:
- Що називають трикутником?
- Чому дорівнює периметр трикутника?
- Що називають медіаною трикутника?
- Що називають бісектрисою трикутника?
- Що називають висотою трикутника?
- Сформулюйте теорему про суміжні кути?
- Який кут називають зовнішнім кутом трикутника?
- Чому дорівнює зовнішній кут трикутника?
- Які види трикутників розрізняють за кутами?
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 2.
Письмово виконати вправи:
-
Один із зовнішніх кутів трикутника дорівнює
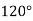 . Знайти внутрішні кути трикутника, не суміжні із даним зовнішнім кутом, якщо вони відносяться як 3:5.
. Знайти внутрішні кути трикутника, не суміжні із даним зовнішнім кутом, якщо вони відносяться як 3:5.
- Виконайте вправу 381 ст. 129.
- Внутрішні кути трикутника відносяться, як 4 : 6 : 5. Знайдіть відношення зовнішніх кутів трикутника, не знаходячи їх величин.
Завдання 3.
Виконайте кросворд, зашифрований QR-коді.

Уроки №4, 5
«Недостатньо тільки отримувати знання, треба знати їх
застосування. Недостатньо тільки бажати, треба діяти»
Й. Гете, німецький письменник
Фронтальне опрацювання матеріалу
Сума кутів трикутника
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 1.9 блоку № 3.
- Усно дайте відповідь на питання:
- Трикутником називається....
- Залежно від кутів, трикутники поділяються на такі види:
- Що називають бісектрисою трикутника?
- Що називають медіаною трикутника?
- Що називають висотою трикутника?
- Що називають зовнішнім кутом трикутника?
- Яку властивість має зовнішній кут трикутника?
- Сформулюйте теорему про суму кутів трикутника.
- Чи може у трикутнику бути два тупих кути?
- Чи буде гострокутним трикутник, кути якого дорівнюють 40º і 50º ?
- Чи буде гострокутним трикутник, два кути якого дорівнюють 45º і 55º?
- Який вид трикутника, якщо один з його кутів 910?
- Два кути трикутника дорівнюють 400 і 600. Чому дорівнює третій кут?
Завдання 2.

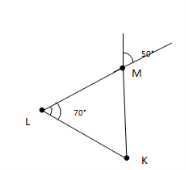
теорема про суміжні кути;
ознака паралельності прямих;
кути, утворені при перетині прямих січною;
суміжні кути;
розгорнутий кут.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Письмово виконати вправи, стор. 128 підручника: 358; 359; 371.
- Допишіть розв’язання задачі (самостійно):
Знайдіть невідомі кути трикутникa MNL.
Вказівка. Згадайте теореми : вертикальні кути рівні; сума суміжних кутів дорівнює 180 º.
<M=……………………………
<K=180°-………………………
Завдання 4.
- Письмово виконати вправи, стор. 130 підручника: 394; 400.
- Самостійно виконай кросворд і ти довідаєшся ім’я визначного математика.
1. Кут величиною 90° називається …
2. Позначення невідомого в рівнянні …
3.Трикутник - це геометрична ...
4.Твердження, яке не потребує доведення …
5.Кут величиною 89 градусів називається ….
6. Дві рівні сторони рівнобедреного трикутника називаються бічними, а третя - ……
7.Трикутники, які можна сумістити накладанням називаються …..
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- Виконай завдання «Склади пару»
1). Трикутник – це геометрична фігура що складається із трьох точок, які не лежать на одній прямій, і ...
2). Трикутник називається рівнобедреним, якщо...
3). Якщо два кути в трикутнику рівні, то...
4). Сума кутів трикутника
5). Зовнішній кут трикутника дорівнює
6). Якщо в трикутнику всі кути по 60°, то
А). Цей трикутник рівносторонній.
Б). Трьох відрізків, які попарно сполучають ці точки.
В). У нього дві сторони рівні.
Г). Цей трикутник рівнобедрений.
Д). Дорівнює 180°
Е) Сумі кутів не суміжних з ним
1-…2-…3-….4-…5-….6-…

Готуємось до індивідуального опрацювання матеріалу
- Знайдіть кути трикутника, якщо їх градусні міри відносяться як 2: 3: 7.
-
За малюнком знайдіть невідомі кути трикутника, якщо
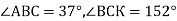
 В
В
![]()
![]()
![]()
А С К
- Одна сторона трикутника на 39 см менша від другої і у 3 рази менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 189 см.
- Два кути трикутника відносяться як 1:3, а зовнішній кут третього кута дорівнює 28°. Знайти кути трикутника.
Урок №8
«Не відкладайте на завтра те,
що можна зробити сьогодні»
Бенджамін Франклін
Фронтальне опрацювання матеріалу
Рівність геометричних фігур. Рівні трикутники
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.12 блоку № 3.
- Усно відповісти на питання:
- Що називають трикутником?
- Чому дорівнює периметр трикутника?
- Що називають медіаною трикутника?
- Що називають бісектрисою трикутника?
- Що називають висотою трикутника?
- Що називають зовнішнім кутом трикутника?
- Чому дорівнює зовнішній кут трикутника?
- Які види трикутників розрізняють за кутами?
- Чому дорівнює сума кутів трикутника?
- Які фігури називаються рівними?
- Як читається властивість рівних фігур?
- Яку властивість мають сторони і кути рівних трикутників?
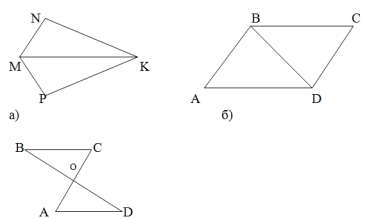
Завдання 2.
Усно виконати вправи за готовими малюнками,
запропоновані вчителем.
 ІІ. Відпрацювання практичних умінь та навичок
ІІ. Відпрацювання практичних умінь та навичок
Письмово розв’язати вправи:
Завдання 3.
Відомо, що пари трикутників на рисунку рівні.
Запишіть відповідні рівності.
Завдання 4.
- Виявіть закономірність у параметрах трикутників. Якими будуть довжини сторін у наступного?
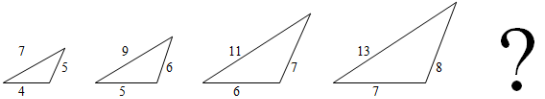
- Зіграйте в гру «Вірю – Не вірю», запропоновану вчителем.
- За допомогою стрілок покажи як рухався гном до виходу, якщо він може пересуватися тільки по клітинках з рівними трикутниками.

Завдання 5.
Вибери правильну відповідь:
- Якщо два трикутники рівні, то в них:
а) всі сторони рівні;
б) всі кути рівні;
в) відповідні сторони рівні та відповідні кути рівні;
г) навпроти рівних кутів лежать рівні сторони.
- Два трикутники будуть рівні, якщо:
а) вони обидва рівнобедрені;
б) їх можна сумістити накладанням;
в) їх назви однакові;
г) вони обидва прямокутні.
-
∆АВС =∆
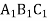 ; АВ = 5 см,
; АВ = 5 см, 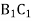 = 8 см,
= 8 см, 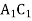 = 4 см, В = 99º. З цього випливає:
= 4 см, В = 99º. З цього випливає:
а) ![]() = 5 см, ВС = 8 см, АС = 4 см,
= 5 см, ВС = 8 см, АС = 4 см, ![]() = 99º;
= 99º;
б) ![]() = 77º , А =
= 77º , А = ![]() ;
;
в) ![]() = 8 см;
= 8 см;
г) АС = 4 см, ВС = 8 см.
-
Відомо, що ∆ PMT= ∆DCF, P = 42°, C = 91°, T = 47°. Знайти невідомі кути трикутників
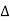 РМТ і
РМТ і 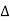 DCF.
DCF.
Урок №9, 10
«Мудріший за все час...»
Фалес Мілетський
Фронтальне опрацювання матеріалу
Перша і друга ознаки рівності трикутників
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.14 блоку № 3.
- Дайте відповіді на запитання, запропоновані вчителем у презентації.
- Гра «так» чи «ні» (якщо «так – плескаєте в долоні).
- Аксіома – це твердження, яке не потребує доведення;
- Сума кутів трикутника 180˚;
- Якщо в трикутнику кут 90˚, то він тупокутний;
- У рівностороннього трикутника усі кути рівні;
- Периметр трикутника – це сума довжин його сторін;
- Трикутники рівні, якщо в них рівні кути і сторони.
Завдання 2.
Виконайте усно вправи:
- Між якими сторонами ▲MNK лежить кут: а) М; б) N; в) К?
- Які ще, окрім позначених, елементи трикутників АВС та MNK на рисунку повинні бути рівними, щоб можна було встановити рівність трикутників за першою ознакою рівності трикутників?
-
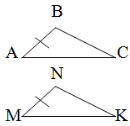
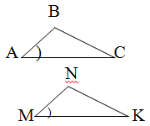
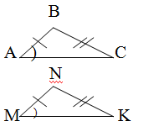 2) 3)
2) 3)
ІІ. Відпрацювання практичних умінь та навичок
Письмово виконати вправи:
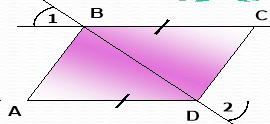 Завдання 3.
Завдання 3.
Письмово виконати вправи за готовими рисунками:
-
Довести:
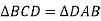 .
.
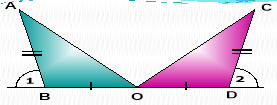
-
Довести:
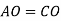 .
.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ
Завдання 4.
Письмово виконайте вправи:
- Відрізки KP і EF перетинаються в точці М так, що КМ = МР і ЕМ = МF. Знайдіть КЕ, якщо РF = 12 см.
- Точка М – середина сторони ВС трикутника АВС. На промені АМ від точки М відкладено відрізок МК, який дорівнює АМ. Доведіть рівність трикутників АСМ і КВМ.
-
На бісектрисі кута А позначили точку D, а на сторонах цього кута – такі точки В і С, що
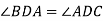 . Доведіть, що ВD = CD.
. Доведіть, що ВD = CD.
Завдання 5.
Виконати тестування, запропоноване вчителем.
Урок №11
«Хто стоїть на місці, той відстає»
Давньоримське прислів'я
Фронтальне опрацювання матеріалу
Третя ознака рівності трикутників
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези блоку № 3.
- Усно відповісти на питання:
- Що називають трикутником?
- Чому дорівнює периметр трикутника?
- Що називають медіаною трикутника?
- Що називають бісектрисою трикутника?
- Що називають висотою трикутника?
- Яку властивість мають сторони і кути рівних трикутників?
- Сформулювати першу і другу ознаки рівності трикутників.
- Сформулювати третю ознаку рівності трикутників.
Завдання 2.
Усно виконати вправи стор. 94 підручника за редакцією Істера О.С.: 376, 377.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
- Письмово виконати вправи, стор. 94 – 95 підручника за редакцією Істера О.С.: 379; 381.
-
Точки
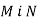 лежать в одній півплощині відносно прямої
лежать в одній півплощині відносно прямої 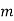 . На прямій
. На прямій 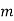 позначено такі точки
позначено такі точки 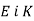 , що
, що 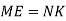 i
i 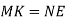 . Доведіть, що
. Доведіть, що 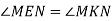 .
.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ
Завдання 4.
Скільки трикутників на малюнку?
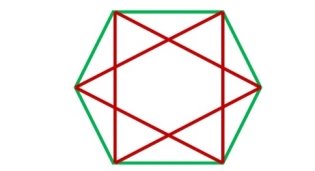
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Трикутник АВС дорівнює трикутнику KLN. KL = 5см, LN = 7см, AC = 9см. Знайдіть решту сторін кожного трикутника.
-
Трикутник АВС дорівнює трикутнику PQR.
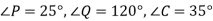 . Знайдіть решту кутів кожного трикутника.
. Знайдіть решту кутів кожного трикутника.
- Відрізки АВ і СМ перетинаються у точці О, причому АО = МО, СО = ВО. Доведіть рівність трикутників АОС і МОВ. Знайдіть периметр трикутника АОС, якщо АС = 2см, СМ = 4см.
- На медіані NK трикутника PNM взято точку L. Відомо, що L рівновіддалена від точок P і M. Довести, що PN = NM.
Урок №13
«У величезному саду геометрії кожний
може підібрати собі букет за смаком»
Давид Гільберт, німецький математик
Внутрішньопредметне узагальнення матеріалу
Трикутники. Ознаки рівності трикутників
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 3.
- Письмово дати відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Два кути трикутника дорівнюють 121° і 32°. Знайдіть міру третього кута трикутника.
|
А |
Б |
В |
Г |
|
34° |
27° |
90° |
45° |
-
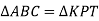 . Знайдіть кути трикутника АВС,
. Знайдіть кути трикутника АВС, 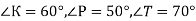 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть периметр трикутника KLM, якщо
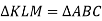 і АВ = 7 см, ВС = 8 см, АС = 6 см.
і АВ = 7 см, ВС = 8 см, АС = 6 см.
|
А |
Б |
В |
Г |
|
10 см |
15 см |
21 см |
8 см |
Завдання 3.
Письмово виконати вправи:
-
У трикутниках АВС і КМР
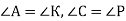 , АС = КР = 9 см, ВС = 5 см, КМ = 6 см. Доведіть рівність трикутників АВС і КМР і знайдіть периметр трикутника АВС.
, АС = КР = 9 см, ВС = 5 см, КМ = 6 см. Доведіть рівність трикутників АВС і КМР і знайдіть периметр трикутника АВС.

 В М
В М
5 6
А 9 С К 9 Р
-
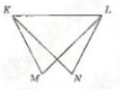 Периметр трикутника дорівнює 70 см. Чому дорівнюють довжини його сторін, якщо одна з них більша від іншої на 10 см і менша від третьої на 5 см?
Периметр трикутника дорівнює 70 см. Чому дорівнюють довжини його сторін, якщо одна з них більша від іншої на 10 см і менша від третьої на 5 см?
-
На малюнку
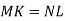 ,
, 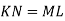 . Доведіть, що
. Доведіть, що 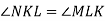 .
.
1


про публікацію авторської розробки
Додати розробку