Міністерство освіти і науки України

Департамент освіти і науки Хмельницької державної адміністрації

Управління освіти і науки Кам’янець-Подільської міської ради

Кам’янець-Подільська спеціалізована загальноосвітня школа І-ІІІ ступенів №1 з поглибленим вивченням німецької мови Хмельницької області 

 

 

 

 

І.І. Теличко вчитель фізики

 

 

 

 

 

 

 

 

 

ФІЗИКА:

ГОТУЄМОСЯ ДО ЗНО

 

Навчальний посібник

 

 

 

 

 

 

 

 

 

 

 

м. Кам’янець-Подільський

                                                                                                      2018                                                 

 

Теличко І.І. - вчитель фізики Кам’янець-Подільської спеціалізованої загальноосвітньої школи І-ІІІ ступенів №1 з поглибленим вивченням німецької мови Хмельницької області.

 

Рецензент:

Ю.М. Смольницький - вчитель фізики Кам’янець-Подільського ліцею.

 

Схвалено методичним об’єднанням вчителів природничо-математичних наук Кам’янець-Подільської спеціалізованої загальноосвітньої школи І-ІІІ ступенів №1 (протокол №2 від 09.11.2018)

 

Теличко І.І. Фізика: готуємося до ЗНО: навчальний посібник. - Кам’янець - Подільський, 2018. - 120 с.

 

 

В посібнику описані вимоги щодо структури тестових завдань і їх оцінки. Наведена програма шкільного курсу та поради до підготовки. Для кожного розділу програми подані основні формули і закони, приклади рішення задач різного рівня складності і завдання для самостійної роботи. В кінці посібника є приклад відповідей на завдання та додатки в яких подано перелік усіх формул, що вивчають в курсі фізики і довідкові таблиці.

Для абітурієнтів, учнів 11 класу, вчителів фізики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

© Теличко І.І., 2018

           

ЗМІСТ

                ВСТУП                                                                                                   4

1.     МЕХАНІКА 9

1.1.      Основи кінематики 9

                                               Завдання для самостійної роботи                                        18

1.2.      Основи динаміки     24

1.3.      Закони збереження в механіці    24

                                               Завдання для самостійної роботи                                        33

1.4.      Коливання і хвилі    37

                                               Завдання для самостійної роботи                                        40

2.     МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА         42

                                               Завдання для самостійної роботи                                        47

3.     ОСНОВИ ЕЛЕКТРОДИНАМІКИ      51

3.1.      Електричне поле      51

                                               Завдання для самостійної роботи                                        57

3.2.      Електричний струм 60

                                               Завдання для самостійної роботи                                        64

3.3.      Магнітне поле          66

                                               Завдання для самостійної роботи                                        69

3.4.      Електромагнітні коливання і хвилі      72 Завдання для самостійної роботи 76

4.     ОПТИКА      78 Завдання для самостійної роботи          84

5.     ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ          87

                                               Завдання для самостійної роботи                                        89

6.     КВАНТОВА ФІЗИКА     90

                                               Завдання для самостійної роботи                                        93

7.     АТОМНА ФІЗИКА         95

                                               Завдання для самостійної роботи                                        97

                ВІДПОВІДІ НА ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ             98

                ДОДАТКИ                                                                                               

                      Додаток 1. ОСНОВНІ ФОРМУЛИ                                                      100

                      Додаток 2. ФІЗИКА У ТАБЛИЦЯХ                                                     113

                ВИКОРИСТАНА ЛІТЕРАТУРА                                                              120

           

 

ВСТУП

ПРОГРАМА ШКІЛЬНОГО КУРСУ ФІЗИКИ

1. МЕХАНІКА

1.1. ОСНОВИ КІНЕМАТИКИ

•      Механічний рух. Траєкторія. Система відліку. Відносність руху. Шлях і переміщення. Рівномірний і рівноприскорений рух. Швидкість руху. Додавання швидкостей. Прискорення. Графіки залежностей кінематичних величин від часу при рівномірному і рівноприскореному рухах.

•      Рівномірний рух по колу. Період і частота обертання. Кутова швидкість.

Доцентрове прискорення.

1.2. ОСНОВИ ДИНАМІКИ

•      Перший закон Ньютона. Інерціальні системи відліку. Маса. Сила. Додавання сил. Другий закон Ньютона. Третій закон Ньютона.

•      Гравітаційні сили. Закон всесвітнього тяжіння. Сила тяжіння. Центр мас. Перша космічна швидкість.

•      Сила пружності. Закон Гука. Вага тіл, що рухаються з прискоренням вертикально. Невагомість.

•      Сила тертя. Коефіцієнт тертя.

•      Момент сили. Умови рівноваги тіл. 

•      Сила Архімеда. Умови плавання тіл. 

•      Рух під дією сил тяжіння, тертя, пружності: рух штучних супутників, рух по параболі, на поворотах, по коловій траєкторії у вертикальній або горизонтальній площинах, по похилій площині.

1.3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ

•      Імпульс тіла (кількість руху). Закон збереження імпульсу. Реактивний рух.

•      Залежність тиску рідини від швидкості її течії. Підіймальна сила крила літака. 

•      Механічна робота і потужність. Кінетична і потенціальна енергія. Закон збереження енергії в механічних процесах.

1.4. МЕХАНІЧНІ КОЛИВАННЯ

•      Гармонічні коливання. Амплітуда, період. частота, фаза коливань. Вільні й вимушені коливання. Перетворення енергії в гармонічних коливаннях. Резонанс. 

•      Математичний маятник. Період коливань математичного маятника. Пружинний маятник. Період коливань математичного і пружинного маятників. 

Поширення механічних коливань у пружних середовищах. Поперечні і поздовжні хвилі. Довжина хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення та періодом (частотою). 

•      Звукові хвилі. Швидкість поширення звуку. Гучність звуку та висота тону. Акустика. Акустичний резонанс. Луна. Інфразвуки. Ультразвуки.

2. МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА

•      Основні положення молекулярно-кінетичної теорії та їх дослідне обґрунтування. Маса і розміри молекул. Дослід Штерна. Броунівський рух. Взаємодія атомів і молекул речовини у різних агрегатних станах. 

•      Ідеальний газ. Основне рівняння МКТ ідеального газу. Температура та її вимірювання. Абсолютна температурна шкала. Рівняння стану ідеального газу (рівняння Менделеєва-Клапейрона). Ізопроцеси в газах.

•      Насичена і ненасичена пара. Кипіння. Залежність температури кипіння рідини від тиску. Вологість повітря. Вимірювання вологості повітря.

•      Властивості поверхні рідини. Поверхневий натяг рідин. Сила поверхневого натягу. Змочування. Капілярні явища.

•      Кристалічні та аморфні тіла. Поняття про рідкі кристали. Механічні властивості твердих тіл. Види деформації. Модуль Юнга.

•      Внутрішня енергія тіла і способи її зміни. 

•      Кількість теплоти. Нагрівання та охолодження речовини. Питома теплоємність. Плавлення та тверднення. Питома теплота плавлення. Випаровування та конденсація. Питома теплота пароутворення. Згоряння. Питома теплота згоряння. Рівняння теплового балансу.

•      Робота газу. Перший закон термодинаміки і його застосування до ізопроцесів. Адіабатний процес. Необоротність теплових процесів. 

•      Принцип дії теплових двигунів. ККД теплових двигунів і його максимальне значення. Шляхи підвищення ККД. Екологічні проблеми, породжені використанням теплових двигунів.

3. ОСНОВИ ЕЛЕКТРОДИНАМІКИ

3.1. ЕЛЕКТРИЧНЕ ПОЛЕ

•      Електричний заряд. Закон збереження електричного заряду. Закон Кулона. 

•      Електричне поле. Напруженість електричного поля. Принцип суперпозиції полів. 

•      Провідники в електричному полі. Електростатичний захист. 

•      Діелектрики в електричному полі. Діелектрична проникність речовини.

Робота електричного поля під час переміщення електричного заряду. Потенціал і різниця потенціалів. Напруга. Зв’язок напруженості електричного поля з напругою. 

•      Електроємність. Конденсатори. Види кoнденсаторів. Ємність плоского конденсатора. З’єднання конденсаторів. 

•      Енергія електричного поля.

3.2. ЕЛЕКТРИЧНИЙ СТРУМ

•      Електричний струм. Умови, необхідні для існування струму.

•      Електрорушійна сила джерела струму. Закон Ома для  повного кола. Опір. Послідовне і паралельне сполучення провідників. Робота і потужність електричного струму.

•      Електричний струм в металах. Електронна провідність металів. Залежність опору від температури. Надпровідність. 

•      Електричний струм у розчинах і розплавах електролітів.  Закони електролізу. Застосування електролізу.

•      Електричний струм у вакуумі. Термоелектронна емісія. Діод. Електроннопроменева трубка.

•      Електричний струм у газах. Самостійний і несамостійний розряди. Використання газових розрядів у техніці. Плазма.

•      Електричний струм у напівпровідниках. Напівпровідники. Власна і домішкова провідність напівпровідників. Залежність електропровідності від температури і освітленості. Напівпровідниковий діод і транзистор, їх використання. Використання напівпровідникових приладів у техніці.

3.3. МАГНІТНЕ ПОЛЕ

•      Взаємодія струмів. Магнітне поле. Індукція магнітного поля. Закон Ампера. Сила Лоренца. 

•      Магнітні властивості речовин. Магнітна проникність. Феромагнетизм.

•      Електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції. Правило Ленца. Самоіндукція. Індуктивність. Енергія магнітного поля.

3.4. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ

•      Гармонічні коливання. Амплітуда, частота, період, зміщення, фаза коливань. Вільні і вимушені електромагнітні коливання в коливальному контурі. Власна частота коливань. Формула Томсона. Перетворення енергії в гармонічних коливаннях.

•      Вимушені електричні коливання. Змінний електричний струм. Генератор змінного струму. Резонанс у колах змінного струму. Автоколивання.

Трансформатор. Холостий хід. Коефіцієнт трансформації. Передача електричної енергії на відстані.

•      Електромагнітне поле. Електромагнітні хвилі та швидкість їх поширення.

•      Принцип радіозв’язку. Найпростіший радіоприймач. 

•      Шкала електромагнітних хвиль. Електромагнітне випромінювання електромагнітних хвиль з різних діапазонів. Властивості та застосування цих випромінювань.

4. ОПТИКА

•      Прямолінійне поширення світла. Швидкість світла та її вимірювання. Закони відбивання світла. Повне відбивання. Побудова зображень у плоскому дзеркалі. 

•      Закони заломлення світла. Абсолютний і відносний показники заломлення світла. Дисперсія світла. 

•      Лінза. Оптична сила лінзи. Побудова зображень у лінзах.

•      Інтерференція світла. Досліди Френеля. Дифракція світла. Дифракційна решітка. Вимірювання довжини світлової хвилі за допомогою дифракційної решітки.

•      Поляризація світла.

5. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ

•      Принцип відносності Ейнштейна. Швидкість світла у вакуумі як гранична швидкість взаємодій. Зв’язок між масою та енергією.

6. КВАНТОВА ФІЗИКА

•      Фотоефект та його закони. Квант світла. Рівняння Ейнштейна для фотоефекту. Стала Планка. Застосування фотоефекту в техніці.

Вакуумний та напівпровідниковий фотоелементи.

•      Фотон. Енергія та імпульс фотона. Тиск світла. Досліди Лебедєва.

•      Корпускулярно-хвильовий дуалізм.

7. АТОМНА І ЯДЕРНА ФІЗИКА

•      Класичні уявлення про будову атома. Дослід Резерфорда.

•      Квантові постулати Бора. Випромінювання і поглинання світла атомом. Неперервний та лінійчатий спектри. Спектральний аналіз. Лазер.

•      Склад ядра атома. Ізотопи. Енергія зв’язку атомних ядер. Термоядерні реакції.

Поділ ядер урану. Ядерні реакції. Ланцюгова реакція. Ядерний реактор. Енергетичний вихід ядерної реакції. Проблеми розвитку ядерної енергетики в Україні.

•      Радіоактивність. Альфа-, бета- і гама-промені. Методи реєстрації іонізуючих випромінювань. Поглинена доза випромінювання. Біологічна дія радіоактивного випромінювання та захист від нього.

Поради щодо підготовки до ЗНО

Готуючись до ЗНО, уважно прочитайте теоретичний матеріал шкільного підручника. Закони, правила, означення фізичних величин і одиниці їх вимірювання запам’ятайте. Уясніть для себе всі малюнки і графіки, наведені в параграфі. Спробуйте їх відтворити самостійно і за їх допомогою поясніть все те, що описано у цьому параграфі.

Дайте відповіді на питання, наведені в кінці параграфу чи розділу. Якщо ви не впевнені у правильності своїх відповідей чи не можете дати відповідь на питання, отримайте консультацію у вчителя. Не бійтеся запитувати – краще всі незрозумілі питання з’ясувати до ЗНО.

Виконайте завдання вправ і звірте свої результати з відповідями в кінці підручника.

Рекомендації до виконання тестових завдань

Нижче наводимо основні формули і математичні співвідношення між фізичними величинами та приклади рішення задач з кожного розділу програми. В кінці кожного розділу є завдання для самостійної роботи. В заключному розділі подані примірні зразки завдань і приклади відповідей на них.

           

1.       МЕХАНІКА

1.1. ОСНОВИ КІНЕМАТИКИ

1. Положення точки на траєкторії визначається його координатою х, яка рівна відстані рухомої точки від деякої нерухомої точки О, що лежить на

траєкторії і прийнята за початок координат. Вираз виду

                                                                                                                   (1.1)

називається кінематичним рівнянням руху. Якщо точка рухається по прямій в одному напрямку, то координата х співпадає з довжиною шляху s, який пройшла точка від початку координат. В цьому випадку рівняння руху: s = f(t). Якщо ж в деякий момент часу точка змінює напрям руху на зворотній, то координата і шлях не співпадають, бо координата з цього моменту починає зменшуватись, а шлях продовжує зростати.

                  Середня швидкість                                                               (1.2)

де: x - зміна координати х за проміжок часу t. Вираз (1.2) втрачає зміст, якщо інтервал x містить точку, в якій напрям руху змінюється на зворотній. В цьому випадку .

                  Миттєва швидкість                                                              (1.3)

Середнє прискорення   (1.4) де: v - зміна швидкості за проміжок часу t. 

                    Миттєве прискорення:                                                      (1.5)

                   2. Рівняння рівноприскореного руху:              (1.6)

де  - відстань рухомої точки від нерухомого тіла (точки О) відліку в момент часу t = 0,  - швидкість точки в цей момент часу. Якщо нерухому точку О вибрати там, де знаходиться рухома точка в момент часу t = 0, то = 0 і

рівняння руху буде:                                                             (1.7)

                   Швидкість рівнозмінного руху                                    (1.8)

Виключивши час з рівнянь (1.7) і (1.8), маємо: 

                                                                                                 (1.9)

Для рівноприскореного руху формули (1.6), (1.7) і (1.9) справедливі, якщо в них замість координати х підставити пройдений шлях s. 

Середня швидкість рівнозмінного руху

                   (1.10) Формули (1.4) і (1.10) справедливі для інтервалу часу, що не включає моменту, в який швидкість змінює знак.

                Прискорення при рівнозмінному русі a = const                               (1.11)

Якщо a > 0, то рух рівноприскорений, коли a < 0 - рух рівносповільнений.

Вільне падіння тіл, і тіл, кинутих вертикально, описуються рівняннями рівнозмінного руху (1.7) - (1.10), замінивши а на g, де g=9,81 м/c².

3.                 Для рівномірного руху:   (1.12) або при х₀= 0    (1.13)  v = const, a = 0.  (1.14)

Якщо тіло проходить кілька ділянок s₁, s₂, …, s_n, маючи на кожній ділянці сталі швидкості v₁, v₂, …, v_n, то середня швидкість на всьому проміжку руху буде:             (1.15)

4.                 Додавання двох векторів швидкостей v₁ і v₂ з кутом  між ними приводить до третього вектора, модуль якого визначається формулою.

                                                        v v12 v22 2v1v2cos                           (1.16)

Криволінійний рух

5.                 Найпростішим прикладом такого руху є рівномірний рух тіла по колу. При рівномірному русі по колу радіуса R основні формули для кутової швидкості , лінійної швидкості v і доцентрового (нормального) прискорення a_n:

             

                               

де:  - кутове переміщення, Т – період, - частота обертання, n - число обертів за секунду.

Нормальне прискорення характеризує зміну швидкості за напрямом, спрямоване до центру кривизни траєкторії і виражається  формулою

                (1.20) де R - радіус кривизни траєкторії.

Для тіла, кинутого під кутом  до горизонту з початковою швидкістю v₀: час польоту:   (1.21)

найбільша висота підйому:              (1.22) дальність польоту:                   (1.23)

 

Рекомендації до розв’язування задач

1.                 Для розв’язування задач з кінематики потрібно знати закон (рівняння) руху точки, яке визначає її положення в будь-який момент часу. Слід встановити характер руху: рівномірний чи рівнозмінний і використати відповідні зв’язки між кінематичними величинами. В більшості задач достатньо записати рівняння для шляху та швидкості.

2.                 В задачах можуть бути задані рівномірні прямолінійні рухи не одного, а кількох тіл по відношенню до системи відліку, пов’язаної з Землею, або іншою системою відліку. В цьому випадку розв’язання задач спрощується, якщо всі рухи розглядати в системі відліку, зв’язаній з одним із рухомих тіл. Тоді слід використати закон додавання швидкостей.

3.                 Якщо матеріальна точка одночасно приймає участь в кількох рухах, то використовують принцип незалежності рухів - кожен з рухів відбувається незалежно від інших.

4.                 Серед задач на рівнозмінний рух значну групу складають задачі на рух точки зі сталим прискоренням. Якщо при цьому вектор прискорення і вектор початкової швидкості лежать на одній прямій, то рух буде рівнозмінним прямолінійним. В іншому випадку точка рухається по кривій другого порядку в площині, яка містить ці вектори. Тут може бути використаний метод графічного розв’язування задач, якщо відомі початкова швидкість і прискорення руху.

5.                 Основним методом рішення задач з кінематики є аналітичний. При цьому від векторної форми запису рівнянь переходять до скалярної, для чого проектують вектори на осі координат. Вибір осей визначається умовою задачі. Варто намагатись, щоб частина проекцій була рівною 0. Це спростить розв’язування рівнянь. Як правило, початок координат суміщають з положенням точки в початковий момент часу.

6.                 Напрями вектора кутової швидкості і обертання тіла пов’язані правилом правого гвинта.

 

Приклади розв’язування задач

Приклад 1. З якою швидкістю може йти людина під дощем, щоб краплі дощу не падали на ноги? Висота зонта над землею h = 2 м, край зонта виступає вперед на L = 0,3 м, краплини дощу падають вертикально з швидкістю              v_к = 8 м/с. 

Розв’язання: Так, як краплі дощу падають з незначної висоти, то швидкість їх падіння на цьому відрізку шляху будемо вважати сталою. Час падіння краплі знайдемо з виразу для рівномірного прямолінійного руху: 

.

Очевидно, щоб краплі дощу не падали на ноги людини, вона повинна за цей же час пройти шлях, не більший, ніж виступ зонта вперед по напрямку руху, тобто: .

Або, врахувавши вираз для часу падіння, маємо: 

 

Відповідь: Швидкість людини не має бути більшою 1,2 м/с.

Приклад 2. По нерухомому ескалатору метро пасажир піднімається за     t₁ = 120 с, а по рухомому при тій же швидкості відносно ступеней за t₂ = 30 с. Знайти час t₃ підйому нерухомого пасажира по рухомому ескалатору.

Розв’язання: Позначимо швидкість пасажира через v_п, а швидкість ескалатора - через v_е. У кожному з випадків пасажир переміщується на однакову відстань, яку позначимо через s. Так, як рухи рівномірні, то маємо:

•    у першому випадку час руху , тому          (1)

•    у другому випадку, коли рухаються і пасажир, і ескалатор, то          

, звідки                                                            (2)

•    у третьому випадку нерухомий пасажир, тому  або 

                                                                                                         (3)

Прирівняємо попарно вирази (1), (2) і (1), (3):

                (4)             (5)

Знайдемо з (5) вираз швидкості руху ескалатора  і підставимо

його у (4). Маємо: ,                                                     (6)

Звідси отримуємо вираз для обчислення часу підйому по рухомому ескалатору нерухомого пасажира: 

.

Відповідь: Нерухомого пасажира ескалатор підіймає за 40 с.

Приклад 3. З міст А і Б, відстань між якими 100 км, одночасно з інтервалом 20 хв. у зустрічних напрямках відправляються автобуси. З міста А вони рухаються з середньою швидкістю 40 км/год, а з міста Б 60 км/год. Скільки автобусів зустрінуть пасажири третіх автобусів? 

Розв’язання. Використаємо графічний метод. Для цього побудуємо графіки руху автобусів (мал. 1). Тепер підрахуємо, скільки

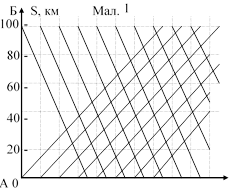
                     1               2                3  t, год   

разів графіки руху третіх автобусів перетинається з графіками руху зустрічних автобусів і отримаємо відповідь: пасажир, що рухається з міста А до Б, зустріне 10, а з міста Б до А - 6 автобусів. 

Спробуйте задачу розв’язати аналітично і порівняйте результати.

Приклад 4. З пунктів А і В, відстань між якими а, одночасно починають рухатись два кораблі з швидкостями v₁ і v₂ (v₂ > v₁). Вектори швидкостей утворюють з відрізком АВ однакові кути  = 45. Вважаючи рух кораблів рівномірним і прямолінійним, знайти найменшу відстань між ними.

Розв’язання: Розглянемо два способи рішення задачі, які відрізняються вибором системи відліку.

Аналітичний        метод.         Нехай         рух    кораблів відбувається в системі відліку, зв`язаної з Землею. Спочатку відстань між ними буде зменшуватись, а потім почне зростати. Щоб знайти найменшу відстань s_min між кораблями, використаємо загальний метод дослідження функції на екстремум. Для цього розглянемо положення

кораблів через довільний проміжок часу t після початку їх руху і знайдемо відстань між ними, як функцію часу. З мал. 4(а) маємо, що:

.

Позначимо b = OA = OB, тоді:

                                     .               (1)

Щоб знайти мінімум функції s = f(t), продиференціюємо її по часу і прирівняємо до нуля похідну:

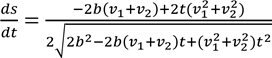                                                .                       (2)

Знаменник дробу не може бути рівним нулю, тому прирівнюємо до нуля чисельник дробу.

Звідси час,що відповідає найменшій відстані s_min, буде: t.

Підставимо це значення часу в (1) і отримаємо відповідь:

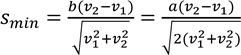                                                                             (3)

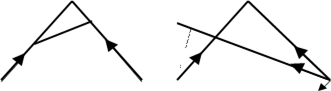
Графічний метод.         Скористаємось    системою    відліку,       пов’язаною, наприклад, з першим кораблем. В такій системі відліку перший корабель буде нерухомим, а рух другого буде складним: з швидкістю v₂ відносно Землі і з швидкістю

      а)      О                 Мал. 2             О      б)

                             N C

         M

   v₁                   v₂        v₁                    v₂  A B  A                          v         B   v`₁

 v'₁=v₁ разом з Землею відносно першого корабля (мал. 2, б). Швидкість результуючого        руху           виразиться вектором    v,       причому                

Мінімальною відстанню між кораблями буде

довжина перпендикуляра АС, опущеного на напрям вектора v. Розрахунок, побудований на подібності прямокутних трикутників, дає відповідь:

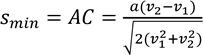                                                                              (4)

Бачимо, що вирази (3) і (4) однакові. 

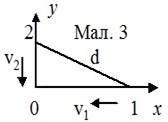Приклад 5. Точки 1 і 2 рухаються вздовж взаємноперпендикулярний осей х і у до початку координат зі сталими швидкостями v₁ = 2 см/с і v₂ = 4 см/с. У момент часу t=0 їх відстані від початку координат: s₁=10 см і s₂=5 см. 

Знайти найменшу відстань між точками.

Розв’язання: В момент часу t відстань між точками буде (мал. 3):

.

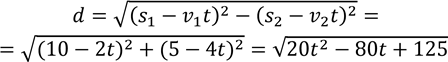Під коренем записано квадратний тричлен, з якого можна виділити повний квадрат: 20t² - 80t+125 = 5[(2t - 4)² + 9].

Зрозуміло, що цей вираз буде найменшим, якщо вираз у дужках буде рівний 0, тобто, коли t = 2. Підставивши значення t у вираз для відстані d, маємо, що d_min = 6,7 (см).

Відповідь: d_min = 6,7 см

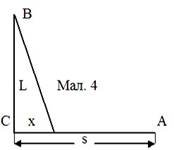Приклад 6. На березі моря проходять змагання. Стартуючи з точки А на березі моря (мал.4), кожен учасник повинен досягти буйка В, розташованого на відстані L = 120 м від берега. Лінію берега можна вважати прямою. Відстань від старту А до основи перпендикуляра ВС s = 200 м. З якої точки берега найвигідніше пливти до буйка, якщо швидкість бігу спортсмена v₁ = 13 км/год, а швидкість плавання у воді v₂ = 5 км/год? 

Розв’язання. Позначимо через х відстань від точки С до того місця, звідки учасник змагань починає пливти до буйка. Тоді учасник пробігає відстань s  x, а пропливає відстань L²  x² . Загальний час руху від старту А до буйка В буде:

.

Якщо довжину відрізка х збільшити на малу величину х, то час руху стане рівним: .

Зміна часу руху буде:

                                                                                     x             L²  (x x)²  L²  x²

t  t₁  t            v1     v2

                                                                  2x x                           1      

xv [ L2  (x x)2  L2  x2]  v1.

2

Виконавши математичні перетворення і, враховуючи, що x << x, знехтуємо величиною x₂. Тоді отримаємо вираз:

                                                                                                              x              1

                                                                              t  (          2        x2  v1)x^.

v2 L 

Оскільки x > 0, то знак t співпадає зі знаком виразу в дужках. При малих х (х  0) вираз в дужках від’ємний, а це значить, що t зменшується з ростом х. При x >> L вираз в дужках додатній, і час збільшується з ростом х. Оскільки функція t змінюється неперервно з ростом х, то існує таке значення х_m, при якому t перетворюється в нуль. Це значення х_m і буде відповідати найменшому часу t.

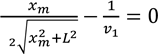
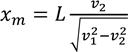
Тобто: . Звідси: 

 

Підставивши числові значення, маємо, що х_m = 50 (м).

Відповідь: х_m = 50 м.

Приклад 7. Літак в момент зльоту повинен мати швидкість руху                v = 100 м/с. Визначити час розбігу і прискорення, якщо довжина розбігу             s = 600 м. Рух літака вважати рівноприскореним.

Розв’язання: Враховуючи, що літак починає рух зі стану спокою (v_o = 0), запишемо рівняння для зміни швидкості і шляху: v ,

де а - прискорення і t - час руху. З першого рівняння прискорення  підставимо у вираз шляху: .

Звідки:  або  

                  Підставимо це значення у вираз для прискорення: 8,33 (м/c²).

Відповідь: t = 12 c, a = 8,33 м/c².

Приклад 8. З башні висотою Н = 19,6 м горизонтально кинули тіло з швидкістю v_o = 10 м/с. Записати рівняння траєкторії тіла. Яка за величиною і напрямком швидкість тіла в момент падіння? Яка далекість польоту? Опором повітря знехтувати.

Розв’язання:. Тіло одночасно приймає участь у двох рухах - рівномірному у горизонтальному напрямку (нехтуємо опором повітря) та рівноприскореному без початкової швидкості у вертикальному напрямі (мал. 5). Запишемо рівняння рухів:  x = v_ot, y .

Виключимо з рівнянь час і отримаємо рівняння траєкторії. Для цього визначимо t з першого рівняння і підставимо у друге. 

t .

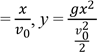Або: y - рівняння параболи.

За принципом незалежності рухів швидкість тіла у горизонтальному напрямку буде рівна швидкості кидання: v_г = v_o і не змінюватиметься з часом. Швидкість вертикального руху буде зростати лінійно з часом від 0 до v_в: v_в = gt. Час польоту буде рівний часу падіння. Його знайдемо з рівняння зміни висоти тіла: H . Звідси:

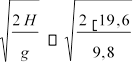
t    2(c)

Дальність польоту: s = v_ot = 10·2 = 20 (м).

Вертикальна швидкість в момент падіння: v_в = 9,8·2 = 19,6 (м/с). Повна швидкість:

      (м/с).     Кут     вектора     повної

швидкості з горизонтом визначимо з прямокутного

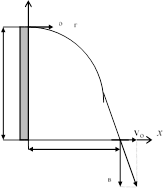      y                     v =v

   Н

                          s 

               Мал. 5 v       v

трикутника, катети якого рівні горизонтальній та вертикальній швидкості, а

гіпотенуза - повній швидкості тіла (мал. 5). Тоді: 1,96. Маємо, що  = 63.

 м/c,  = 63, s = 20 м.

Приклад 9. Лисиця біжить прямолінійно і рівномірно з швидкістю v₁. За нею женеться собака, швидкість якої v₂ стала за величиною і весь час орієнтована на лисицю. В той момент, коли швидкості v₁ i v₂ були перпендикулярними, відстань між лисицею і собакою складала L. Яким було прискорення собаки в цей момент?

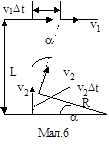Розв’язання. Абсолютна величина швидкості собаки стала, змінюється лише її напрям, тому прискорення собаки направлене перпендикулярно до вектора швидкості. Скористаємось тим, що будь-яку траєкторію точки за короткий проміжок часу можна вважати дугою кола. Тоді прискорення собаки буде являти собою доцентрове прискорення, рівне: , де R - радіус кола, яким можна замінити дійсну траєкторію собаки.

Розглянемо переміщення собаки за малий час t. За цей час вектор швидкості собаки повернеться на кут  такий, що   (мал. 6). З другого боку, лисиця за час t переміститься на відстань v₁t = L, бо вектор швидкості собаки весь час орієнтований на лисицю. Тому: 

. Тоді: R = . 

.

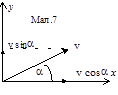Приклад 10. Футболіст вдарив по м’ячу, надавши йому швидкості v під кутом  = 30 до горизонту, і потрапив у нижній кут воріт. Якби він вдарив по м’ячу в тій же точці поля і під тим же кутом до горизонту, але з швидкістю, на 5% більшою, то потрапив би у верхню штангу воріт. Знайти швидкість, з якою починає рухатись м’яч, якщо висота воріт Н = 2 м.

Розв’язання:. Запишемо кінематичні рівняння руху. По горизонталі вздовж осі х м’яч рухається рівномірно з швидкістю v₁ = v cos, а вздовж осі у - рівноприскорено з прискоренням g, направленим донизу і початковою швидкістю v₂ = v sin (мал. 7). Тому: x = vt cos, y=vt sin -.

В момент t_o падіння на Землю у = 0 і x = s, де s - далекість польоту.

Значить: s = vt_o cos,                                                                                      (1)

                                                             0 = vt_o .                                      (2)

Якби м’яч почав рухатись з швидкістю, на 5% більшою швидкості v, тобто з швидкістю 1,05v, то його координати х і у мінялися б з часом так:           x . 

В момент удару м’яча об верхню штангу воріт його координата х була б рівною s, а координата у - висоті воріт Н:

                                                         s = 1,05vt₁ cos,                                             (3)

                                                       H .                                     (4)

Рішимо систему рівнянь (1) - (4). З рівняння (2) знайдемо час польоту

м’яча у першому випадку: t_o ^. Поділимо рівняння (3) на рівняння (1):

.

Звідки: t.

Підставимо значення t₁ в рівняння (4) і отримаємо:

 

Відповідь: v = 19,8 м/c. 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Прямолінійний рівномірний рух

Нижчий рівень

1.1. Водій автобуса помітив, що лічильник показував 15951 км. Через дві години на лічильнику знову було найближче число, яке читалось вперед і назад однаково. Знайти середню швидкість руху автобуса.

1.2. Дві прямі дороги перетинаються під кутом 60. Від перехрестя одночасно по цих дорогах віддаляються два автомобілі: один з швидкістю        v₁ = 60 км/год., а другий з швидкістю v₂ = 80 км/год. З якою швидкістю один автомобіль віддаляється від іншого?

1.3. Два літаки одночасно вилітають з аеродрому у взаємно перпендикулярних напрямках: один з швидкістю 300 км/год, а другий - з швидкістю 400 км/год. Як змінюється з часом відстань між літаками? Якою вона буде, коли перший літак пролетить 900 км?.

1.4. Віддаль між містами А і Б 100 км. Рухаючись від А до Б, автомобіль проїхав першу половину шляху з швидкістю 40 км/год, а другу - з швидкістю 60 км/год. Рухаючись назад, він проїхав першу половину часу з швидкістю      60 км/год, а другу половину часу - з швидкістю 40 км/год. Знайти середні швидкості руху автомобіля в обох випадках. 

1.5. Рухаючись по колу радіусом 60 м, велосипедист подолав 1/3 його довжини, а потім проїхав в напрямку центра кола відстань, рівну половині радіуса. Визначити шлях і переміщення велосипедиста.

1.6. Два потяги рухаються в одному напрямку паралельними коліями. Відстань між ними зростає на 3 м кожні 5 с. Знайти швидкість першого потягу, якщо вона вдвічі більша швидкості другого потягу.

1.7. Точка рухалась 15 с з швидкістю 5 м/с, 10 с з швидкістю 8 м/с і 6 с з швидкістю 20 м/с. Знайти середню швидкість руху точки. 

1.8. Визначити швидкість течії річки, якщо швидкість пароплава за течією 25 км/год, а проти течії 14 км/год. Яка швидкість пароплава відносно води?

1.9. Відстань між містами А і Б 250 км. Одночасно з обох міст назустріч виїжджають два автомобілі, рух яких вважаємо рівномірним. Автомобіль з міста А рухається з швидкістю 60 км/год, а з міста Б - з швидкістю 40 км/год. Побудувати графіки залежності шляху від часу для обох автомобілів і за графіком знайти час і місце їх зустрічі.

Оптимальний рівень

1.10. Риболов, що пливе рікою проти течії, навпроти дерева загубив запасне весло. Через 0,5 год він це виявив і, повернувшись назад, наздогнав весло в 3 км від дерева. Яка швидкість течії річки, якщо риболов, рухаючись вгору і вниз по річці, гріб однаково?

1.11. Йдучи до школи, учень помітив, що кожні 6 хв. його наздоганяє автобус, а кожні 3 хв. повз нього проходить зустрічний автобус. З яким інтервалом від кінцевих зупинок відходять автобуси, якщо рух їх вважати рівномірним?

1.12. Зустрічні потяги мають швидкості v₁ = 36 км/год і v₂ = 54 км/год. Пасажир першого потягу помітив, що другий рухається повз нього протягом     6 с. Яка довжина другого потягу?

1.13. Човен рухається перпендикулярно до течії з швидкістю 2 м/с відносно води. Швидкість течії 1 м/с. Знайти величину і напрям швидкості човна відносно берега.

                 1.14.     Човен     перепливає     ріку     шириною     250     м     у     напрямі,

перпендикулярному до течії. Швидкість течії 0,8 м/с. Яка швидкість і напрям руху човна відносно берега, якщо течія віднесла його за час переправи на      100 м?

Вищий рівень

1.15. Катер, швидкість якого у стоячій воді 15 км/год, треба переправити через річку найкоротшим шляхом. Швидкість течії 5 км/год. Під яким кутом до течії повинен рухатись катер?

1.16. Пароплав пливе на захід з швидкістю 6,5 м/с. Вітер дме з південного заходу зі швидкістю 3,5 м/с. Яку швидкість вітру зареєструють прилади на пароплаві? Яким буде напрям вітру відносно курсу пароплава? Якісні завдання

1.17. Для яких рухів тіла модуль результуючого переміщення завжди співпадає з пройденим шляхом?

А) для руху по колу;

Б) для рівномірного і прямолінійного руху;

В) для будь-якого руху по одній з координатних осей; Г) для прямолінійного рівноприскореного руху;

Д) таких рухів немає.

1.18. Чи може для якогось виду руху тіла модуль вектора переміщення бути:

А) більшим від пройденого шляху;

Б) меншим від пройденого шляху;

В) дорівнювати нулю;

Г) дорівнювати пройденому шляху?

1.19. Як рухаються кораблі один відносно одного, якщо модуль їх відносної швидкості:

А) дорівнює нулю;

Б) збільшується;

В) зменшується;

Г) не змінюється?

1.20. Тіло здійснило два послідовних переміщення з модулями 2 м і 3 м.

Яким може бути модуль результуючого переміщення?

А) 5 м; Б) більшим 5 м; В) від 1 м до 5 м; Г) меншим 5 м.

 

 

Рівнозмінний рух

Нижчий рівень

1.21. Рухаючись рівноприскорено від зупинки, автобус на перших 100 м досяг швидкості 10 м/с. Визначити її зміну на наступних 100 м, якщо прискорення не зміниться.

1.22. Трамвай, відходячи від зупинки, рухався з прискоренням 0,5 м/с². Через який час і на якій відстані від початку руху його швидкість буде             54 км/год? Знайти середню швидкість руху та швидкість в кінці 10-ї секунди.

1.23. Рухаючись з прискоренням 0,3 см/с², велосипедист на шляху 100 м збільшив швидкість у 4 рази. За який час це відбулось?

1.24. Два автомобілі рухаються назустріч один одному з швидкостями 6 м/с і 8 м/с. Коли між ними залишилось 60 м вони почали гальмувати з прискореннями 0,1 м/с² і 0,2 м/с² відповідно. Якою була відстань між ними після зупинки?

1.25. Визначити початкову швидкість автомобіля, якщо при гальмуванні протягом 25 с на відстані 500 м він зменшує швидкість до 54 км/год. Яке прискорення руху? Знайти швидкість в кінці 10-ї секунди гальмування.

1.26. Під час аварійного гальмування автомобіль, що рухався з швидкістю 72 км/год, зупинився через 4 с. Знайти шлях і прискорення такого руху. Оптимальний рівень

1.27. За восьму секунду, рухаючись з стану спокою, тіло пройшло 30 м. Яку відстань воно пройшло за вісім секунд?

1.28. На шляху 250 м показ спідометра автомобіля змінився з 54 до         36 км/год. Вважаючи прискорення сталим, знайти швидкість автомобіля на середині цього шляху.

1.29. Лижник спускається з гори довжиною 125 м. Скільки часу займе спуск, якщо прискорення 0,4 м/с². Якою буде кінцева швидкість лижника?

1.30. Два велосипедисти, рухаються назустріч: один з них, маючи швидкість 5,4 км/год, спускається з гори з прискоренням 0,2 м/с², другий, маючи швидкість 18 км/год, піднімається вгору з прискоренням (0,2 м/с²). Через який час вони зустрінуться?

1.31. Куля вилітає з ствола гвинтівки з швидкістю 720 м/с. З яким прискоренням вона рухається у стволі, якщо довжина ствола 40 см?

1.32. Над аеродромом пролітає транспортний літак з сталою швидкістю 940 км/год. В цей же момент у тому ж напрямку стартує реактивний літак з прискоренням 10 м/с². Через який час і на якій відстані реактивний літак наздожене транспортного?

1.33. Куля вилітає в горизонтальному напрямі з швидкістю 300 м/с. На скільки вона знизиться, якщо відстань до мішені 500 м?

1.34. Стріла випускається лучником горизонтально з швидкістю 120 м/с на висоті 1,5 м над землею. На якій відстані вона впаде на землю? Вищий рівень

1.35. Тіло, що рухалось горизонтально з швидкістю 3 м/с, пружньо ударяється об стінку на висоті 20 м над землею. На якій відстані від стінки впаде тіло після відскоку?

1.36. Дальність польоту тіла, яке кинули в горизонтальному напрямку з швидкістю 10 м/с, дорівнює висоті, з якої його кинули. Знайти цю висоту.

1.37. Тренуючись перед змаганнями, спортсмен цілиться в мішень, підвішену на нитці. В якому напрямку він повинен стріляти, щоб влучити у мішень, якщо в момент пострілу нитка обривається і мішень починає падати? Відстань до мішені 100 м, куля вилітає з швидкістю 500 м/с. Опором повітря знехтувати.

1.38. З плотини ГЕС вертикально падають одна за одною дві краплі. Через 2 с після початку падіння другої краплі відстань між ними була 25 м. На скільки раніше почала падати перша крапля, ніж друга?

1.39. З однієї точки одночасно кинули два тіла з однаковими швидкостями v_o: одне вертикально вгору, а друге - вертикально вниз. На якій відстані одне від одного будуть тіла через час t? Опір повітря не враховувати.

1.40. Падаючи вільно зі стану спокою, тіло за останню секунду польоту пройшло половину всього шляху. З якої висоти падало тіло? Якою буде його кінцева швидкість? 

1.41. Тіло кинули вертикально вгору з швидкістю 20 м/с. Через який час воно буде на висоті 12 м над землею?

1.42. З даху будинку висотою 28 м кинули вгору камінь з швидкістю        8 м/с. Нехтуючи опором повітря, знайдіть час польоту каменя та його швидкість в момент падіння на землю.

1.43. М’яч, кинутий з балкону у вертикальному напрямку, впав на землю через 3 с. Визначити початкову швидкість кидання, якщо висота балкону над землею 14,1 м.

1.44. Тіло вільно падає з висоти 5 м. Разом з ним з висоти 7 м починає падати друге тіло. Якою повинна бути початкова швидкість другого тіла, щоб вони обидва торкнулись землі одночасно?

1.45. З висоти 25 м без початкової швидкості падає тягарець. В ту ж мить з висоти 15 м вертикально вгору кинули другий. З якою початковою швидкістю кинули другий тягарець, якщо він наздогнав першого на висоті 5 м над землею?

1.46. У скільки разів потрібно збільшити початкову швидкість тіла, кинутого вертикально вгору, щоб час підйому його збільшити вдвічі?

1.47. Тіло кинули  горизонтально з швидкістю 30 м/с. Знайти величину і напрям його повної швидкості через 2 с руху.

1.48. Куля пробила два вертикально закріплених листи паперу, відстань між якими 30 м. Отвір у другому листі виявився на 10 см нижче, ніж на першому. Визначити швидкість кулі, якщо в момент дотику до першого листа вона летіла горизонтально. Опором повітря та втратою швидкості при пробої листів нехтувати. 

1.49. Спортсмен кидає спис під кутом 45 до горизонту з швидкістю 12 м/с. На якій відстані впаде спис на землю?

1.50. Волейболіст подає м’яч під кутом 60 до горизонту. Через 1,7 с кут польоту м’яча до горизонту був 30. Знайти початкову швидкість польоту м’яча.

1.51. Хвилинна стрілка годинника має довжину 10 см. Знайти лінійну швидкість руху кінця стрілки.

1.52. Лінійна швидкість точок на краю диска рівна 3 м/с. Точки, розташовані на 10 см ближче до осі обертання, мають лінійну швидкість 2 м/с. Скільки обертів за секунду робить диск? Який радіус диска?

1.53. Дзиґа, що робить 200 об/хв., зісковзує з краю стола і падає на підлогу. Скільки обертів вона зробить за час падіння, якщо висота стола 1,2 м.

1.54. На якій широті лінійна швидкість руху точок земної поверхні вдвічі менша, ніж на екваторі? Радіус Землі 6370 км.

Якісні завдання

1.56. Яке положення займе поверхня води у посудині, яка зісковзує з похилої площини зі сталою швидкістю?

А) горизонтальне;

Б) паралельне до площини;

В) негоризонтальне; Г) задача немає рішення.

1.57. Стала сила прискорює вільне тіло зі стану спокою. Чи зростає на сталу величину швидкість тіла:

А) щосекунди; Б) на кожному метрі шляху.

1.58. В яких місцях Землі гравітаційна сила збігається за модулем і напрямом з силою тяжіння?

А) у Києві; Б) В Австралії; В) на полюсах Землі; Г) на екваторі.

1.59. Яким повинне бути мінімальний коефіцієнт тертя, щоб людина пішки рівномірно піднялась по похилій площині з кутом нахилу 45? А) sin 45; Б) cos 45; B) tg 45; Г) ctg 45.

          

1.2. ОСНОВИ ДИНАМІКИ

1.3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ

1.                Другий закон Ньютона в загальному випадку виражається формулою

          F      (1.24) де p = mv - імпульс тіла.

Якщо маса стала, то: F = ma (1.25) де а - прискорення.

Для сталої за величиною і напрямком дії сили зміна імпульсу тіла за проміжок часу t рівна добутку сили на час її дії:

          p = Ft або mv₂  mv₁ = Ft           (1.26) де v₁ i v₂ - початкова і кінцева швидкості на проміжку часу t.

2.                Сила тертя ковзання F_т = kN  (1.27)

де: k - коефіцієнт тертя ковзання, N - сила, з якою тіло притискується до поверхні, по якій воно рухається.

3.                Сила, що діє на матеріальну точку, яка рухається по кривій траєкторії, може бути розкладена на дві складові - тангенціальну і нормальну.

                 Тангенціальна (дотична) сила F_ ,                                 (1.28)



                    Нормальна (доцентрова) сила F_n                                 (1.29)

або    Fn = m2R де  - кутова швидкість. 4. Відцентрова сила інерції (в неінерціальній системі відліку)

(1.30)

          F_вц      (1.31) або    F_вц = m_²R          (1.32)

Ця сила спрямована вздовж радіус-вектора від центра або осі обертання.

5.     Третій закон Ньютона F₁₂ =  F₂₁    (1.33) де F₁₂ і F₂₁ - сили, з якими взаємодіють дві матеріальні точки.

6.     Момент сили відносно осі обертання M = FL     (1.34)

де L - плече сили (найкоротша відстань від осі обертання до напрямку дії сили

F), або ж                                          M = Frsin                                         (1.35) 

де r - відстань від осі обертання до точки прикладання сили F,  - кут між напрямком дії сили і радіус-вектором r, проведеним від осі обертання до точки прикладання сили.

Момент сили вважається додатнім, якщо він повертає тіло проти годинникової стрілки і від’ємним - якщо за годинниковою стрілкою. 

Тіло, що має вісь або точку обертання, буде в рівновазі, якщо алгебраїчна сума моментів сил, прикладених до нього, рівна нулю.

7.     Закон збереження імпульсу: імпульс замкнутої системи є величина n       n

стала:                                   i1pi  const; i1mivi  const                      (1.36)

де і - число матеріальних часток, які входять до замкнутої системи.

Для двох взаємодіючих матеріальних точок, що рухаються вздовж однієї прямої, цей закон буде: 

          m₁v₁+m₂v₂ = m₁u₁+m₂u₂ (1.37) де v₁ i v₂ - швидкості точок до взаємодії; u₁ i u₂ - їх швидкості після взаємодії.

8.     Робота сталої сили:       A = Fscos           (1.38) де  - кут між напрямами сили та переміщення.

Для змінної з часом чи відстанню сили загальна робота визначається сумою робіт на ділянках, в межах яких силу можна вважати сталою (або ж методом інтегрування).

9.     Потужність:         N = ^ (1.39)



або                                                 N = Fvcos                                           (1.40) 

10.                        Кінетична енергія точки або тіла, що рухається поступально:

                                                            Е_к                                         (1.41)

11.                        Потенціальна енергія тіла, піднятого на висоту h, набагато меншу радіуса Землі:  Е_п = mgh  (1.42)

12.                        Закон збереження енергії в механіці 

                                                         Е_к + Е_п = const                                           (1.43)

13.                        Робота, виконана зовнішніми силами, що діють на тіло і зміна кінетичної енергії пов`язані співвідношенням:

A   = E = E₂  E          (1.44) 

14.                        Застосування законів збереження енергії і імпульсу для прямого центрального удару кульок:

а) швидкість абсолютно непружних кульок після удару 

                                                  u                                           (1.45)

де m₁ i m₂ - маси кульок, v₁ i v₂ - їх швидкості до удару.

б) робота деформації при абсолютно непружньому ударі:

A   = E = (Е_к1 + Е_к2)  Е_к       (1.46)

де Е_к1 і Е_к2 - кінетичні енергії кульок до удару, Е_к - їх кінетична енергія спільного руху після удару, Е - зміна кінетичної енергії в результаті удару.

в) швидкості абсолютно пружніх кульок після удару:

                                                     u                                  (1.47)

                                                          u                             (1.48)

 

Поради до розв’язування задач

1.                 Важливо пам’ятати, що другий закон Ньютона, виражений формулою (1.24), справедливий лише в інерціальних системах відліку. Якщо в задача вивчається рух тіл відносно поверхні Землі, то систему відліку, пов`язану з Землею, можна вважати інерціальною.

2.                 Сила тяжіння рівна mg, де m - маса тіла, g - прискорення вільного падіння. Внаслідок добового обертання Землі сила тяжіння дещо відрізняється від сили, з якою тіло притягується Землею. В розв’язуванні задач цим можна нехтувати, якщо  про таке спеціально не вказується в умові.

3.                 Для розв’язання задач з динаміки записують рівняння руху матеріальної точки (тіла), яке виражає другий закон Ньютона. При цьому рекомендується такий порядок дій:

*     виконати малюнок і на ньому зобразити всі сили, що діють на тіло. Вираз «на тіло діє сила» значить, що це тіло взаємодіє з іншим тілом, в результаті чого отримує прискорення. Тому до тіла завжди прикладено стільки сил, скільки є інших тіл, з якими воно взаємодіє. Щоб вірно визначити напрям сил, слід пам`ятати, що сила тяжіння направлена донизу (вертикально); сила реакції опори за відсутності тертя - по нормалі до дотичних поверхонь в точці їх дотику; сила натягу нитки - вздовж нитки в бік точки підвісу.

*     записати другий закон Ньютона у векторній формі;

*     якщо сили діють не вздовж однієї прямої, то слід вибрати дві взаємно перпендикулярні вісі (х і у), які лежать в площині дії сил. Спроектувавши всі вектори, які входять у рівняння, на ці осі, записати другий закон Ньютона у вигляді двох скалярних рівнянь: 

                                                         F_x = ma_x, F_y = ma_y                                 (1.49)

Для прямолінійного руху одну з осей (наприклад, х) направляють вздовж прискорення а, а іншу (у) – перпендикулярно до вектора а. Тоді: а_х = а, а_у = 0 і рівняння (1.49) спрощуються:

                                                           F_x = ma, F_y = 0.                                   (1.50)

У випадку криволінійного руху одну вісь спрямовують вздовж тангенціального прискорення (по дотичній до траєкторії), другу - вздовж нормального прискорення a_n.

Якщо всі сили, що діють на тіло, лежать на одній прямій, і вздовж цієї прямої направлений вектор а, то, вибравши її за вісь проекцій і спрямувавши за напрямком вектора а, зразу отримуємо другий закон у скалярній формі:  

                                                                  F = ma                                            (1.51)

де F - сума проекцій сил, які діють на тіло. В запису рівнянь враховують знаки проекцій.

4. Якщо в задачі вивчається рух тіл, зв’язаних між собою, то рівняння руху записуються для кожного тіла окремо. Крім цього, записують рівняння, які виражають кінематичні умови і пов’язують прискорення окремих тіл системи (наприклад, рівність за модулями прискорень двох вантажів, які підвішені до нерозтяжної нитки, перекинутої через блок). Загальне число рівнянь повинне бути рівним числу невідомих величин.

Якщо тіла зв’язані ниткою, масою якої можна нехтувати, то силу натягу нитки вважають однаковою по всій довжині. В цьому випадку нехтують масою блока, а також силами тертя при обертанні блока.

 

Приклади розв’язування задач

Приклад 11. До кінців однорідного стержня прикладені дві протилежно направлені сили F₁ = 40 H i F₂ = 100 H (мал. 8, а). Знайти силу натягу F стержня у поперечному перерізі, яке ділить стержень на дві частини у відношенні 1:2.

Розв’язання. Якби сили були однакові за величиною, то сила натягу в

                        L                         a)            довільному перерізі стержня була б однаковою і рівною

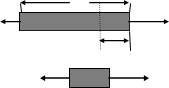  F1                                              F2              силам, що прикладені до кінців стержня. Але, оскільки

 

 сума сил, прикладених до стержня, відмінна від нуля, то

   Мал.8                       L/3

               F F_{2  б})                     стержень буде рухатись з прискоренням, величина і

 напрям якого визначаються з ІІ закону Ньютона, де m -

маса стержня: a                                                                                 (1)

Так, як сили діють вздовж прямої, то їх геометричну суму можна замінити алгебраїчною

                                                                    a                                            (2)

Прискорений рух стержня приводить до того, що сила натягу у різних перерізах буде різною. Для визначення цієї сили застосуємо такий прийом: уявно розділимо стержень у потрібному нам місці на дві частини і відкинемо одну з них, наприклад, ліву. Дію лівої частини на праву замінимо силою натягу F (мал. 8, б). В результаті дії різниці сил (F₂ - F), права частина стержня масою m1 повинна рухатись з прискоренням a , рівним за величиною і напрямком прискоренню, вираженому формулою (2). Вважаючи стержень однорідним, маємо, що і тому: a ,  (3)

Прирівнявши праві частини (2) і (3), знаходимо: F .

Обчислення дає відповідь: F = 80 H.

Приклад 12. Максимально допустима швидкість руху автомобіля по слизькій дорозі на повороті радіуса R складає v_max. На повороті дорога нахилена під кутом  до горизонту. З якою найменшою швидкістю може їхати автомобіль на такому повороті?

         N         (a)              N` (б)                                             Розв’язання. Розглянемо сили, які діють на

      F`_т

F_т                                                      автомобіль. У першому випадку (мал. 9, а): сила тяжіння

                      

               ^{                         }                      mg, сила нормальної реакції з боку дороги N і сила тертя

mg      Мал. 9         mg              F_т = kN (k - коефіцієнт тертя). На максимальній швидкості сила тертя перешкоджає «заносу» автомобіля

на повороті.

У другому випадку (мал. 9, б) сила тертя F'_т = kN' (де N' - сила реакції дороги у цьому випадку) перешкоджає ковзанню автомобіля вниз по площині дороги.

Запишемо рівняння руху автомобіля, спроектувавши всі сили на вертикальну та горизонтальну осі. При русі з v = v_max: 

                         Ncos - mg - F_т sin = 0, або N(cos - ksin) - mg = 0         (1)

При русі з v=v_min: N'cos - mg + F'_тsin = 0, або:

                                              N'(cos + ksin) - mg = 0.                               (2)

В горизонтальній площині автомобіль рухається по колу радіуса R з доцентровим прискоренням . За другим законом Ньютона при русі з v = v_max:

                                                 , або

                                                   ,                                   (3)

а при русі з v , або

                                                   N'.                                   (4)

З рівняння (2) знайдемо N', підставимо в (4) і отримаємо: 

                  . Звідси: .                 (5)

Для відшукання k з рівняння (1) виразимо N і підставимо в (3): 

. Маємо: .

Тоді: . Це і буде відповідь задачі.

Приклад 13. Мотузка довжиною L перекинута через блок так, що її кінці знаходяться на однаковій висоті над землею. Блок трохи повертають і мотузка починає зісковзувати з нього під дією сили тяжіння. Яку швидкість матиме мотузка в момент відриву від блоку?

 У початковий момент центр мас мотузки знаходиться на

відстані  від блоку (мал. 10). В момент, коли мотузка зісковзне з блоку, її центр мас буде на відстані  від блоку. За час руху потенціальна енергія системи «мотузка – Земля» зміниться на величину mg .

З закону збереження енергії слідує, що зміна потенціальної енергії системи веде до зміни її кінетичної енергії, тобто: .

Звідки .

Приклад 14. Двигуни ракети розвивають силу тяги F_т = 2,45·10⁵ Н. Визначити прискорення ракети та вагу космонавта в той момент, коли маса ракети складала М = 5·10³ кг. Маса космонавта m = 70 кг. Ракета рухається вертикально.

Розв’язання. Запишемо ІІ закон Ньютона для руху ракети. В напрямку руху ракети діє сила тяги двигунів F_т. Проти руху (донизу) направлена вага ракети Mg (оскільки m << M, то масою космонавта тут можна знехтувати). За цих умов маємо:

Мa = F_т - Mg, звідки: а .

Вага космонавта - це сила, з якою він діє на сидіння крісла (реакція крісла). Вона буде рівна P = ma + mg = m (a + g). Обчислимо: а = 39,2 (м/с²); Р = 3430 (Н).

Відповідь: а = 39,2 м/с², Р = 3430 Н.

Приклад 15. Кубик висотою h = 10 см і масою М =100 г лежить на горизонтальній підставці. Знизу його пробиває куля масою m = 10 г, яка летить вертикально. За час прольоту через кубик швидкість кулі зменшується з v₁ = 100 м/с до v₂ = 95 м/с. Чи підстрибне при цьому кубик?

Розв’язання. Кубик зможе підстрибнути, якщо сила F, що діє на нього з боку кулі, буде більшою сили тяжіння Mg = 1 H. Знайдемо цю силу. Зміна швидкості руху кулі при прольоті через кубик змінюється мало - всього на 5%.

Тому можна вважати, що сила F стала і не залежить від швидкості кулі.

Імпульс кулі при прольоті через кубик змінюється завдяки дії двох сил - сили тяжіння mg і сили тертя F. Якщо час, за який пролітає через кубик позначити через t, то:

                                                       m(v₁ - v₂) = (F+mg)t                                       (1)

Середня швидкість кулі в кубику v_ср , бо сила опору стала і рух рівнозмінний. Тому:

                                                                                                    (2)

Підставимо (2) в (1) і знайдемо, що:

F = .

Бачимо, що F > Mg, значить кубик підстрибне.

Приклад 16. Циліндр радіуса R розрізаний  на дві

      R

                            Рх однакові частини вздовж його осі. Вага кожної половини                          ^a            2R циліндра рівна Р, а центри ваги знаходяться на відстані а від осі. Щоб циліндр не розпався, через нього перекинули нитку з

            _О                                однаковими вантажами на кінцях (мал. 11). Нехтуючи тертям,

^{Рх  Р    Мал. 11}                              знайти найменшу вагу вантажів, які не допусться розпаду

циліндра. 

Розв’язання. Оскільки положення вантажів симетричне відносно площини розрізу, то достатньо розглянути сили, що діють на одну половину циліндра, наприклад, ліву і моменти цих сил. Вважаючи нитку невагомою і нехтуючи тертям маємо, що натяг нитки однаковий по всій її довжині і рівний вазі вантажу. Позначимо цю вагу через Р_х. Рівняння моментів відносно точки О дотику півциліндра до площини, на якій він лежить, буде: Р_хR + Pa = P_x2R.

Звідки .

Приклад 17. На спокійній воді ставка стоїть човен довжиною L і масою М перпендикулярно до берега, повернутий до нього кормою. На кормі стоїть людина масою m. На яку відстань s наблизиться човен до берега, якщо людина рівномірно перейде з корми на ніс човна? Тертям об воду і опором повітря знехтувати.

Розв’язання. Якщо людина рухається по човну рівномірно, то й човен теж буде наближатись до берега рівномірно, тому

s   = v t         (1) 

де: v - швидкість човна відносно берега t - час руху людини і човна. Напрям переміщення людини приймемо за додатній. Швидкість човна знайдемо з закону збереження кількості руху. В початковий момент човен i людина були нерухомими, тому: 

                                                              Mv - mu = 0                                            (2)

де u - швидкість людини відносно берега; знак «» вказує на те, що швидкість руху людини протилежна швидкості човна. Маємо, що: v   (3)

Час t руху човна рівний часу руху людини по човну, тобто 

t              (4)

де s₁ - переміщення людини відносно берега. Підставивши (4) і (3) в (1),

знайдемо: .

Звідки  

Приклад 18. Тіло масою m = 0,5 кг, закріплене на стержні довжиною        L = 2 м, рівномірно обертається у вертикальній площині навколо осі, роблячи   n = 0,33 об/с. Визначити силу натягу стержня у найвищій  і найнижчій точках траєкторії.

Розв’язання. Тіло рухається по колу під дією сили тяжіння mg, сили F натягу стержня і сили інерції F_i, обумовленою кривизною траєкторії. Запишемо рівняння руху для верхньої А і нижньої В точок траєкторії (мал. 12.). В точці А: mg = F_A + F_i, або:            mg = F_A + m2R.

В точці В: mg + F_i = F_B. або: mg + m2R = F_B де: R = L/2,  = 2n. З цих рівнянь відповідь:

42n2L

FA  mg 2g  1  2,7H; FB  mg 422gn2L  1  7,1H.

Зауваження. Оскільки F_A < 0, то стержень стиснутий, коли тіло проходить точку А. При стержень був би розтягнутий в точці А. 

Приклад 19. Тіло масою m = 20 кг тягнуть по                  y горизонтальній площині з силою F = 120 Н. Якщо           N

сила прикладена до тіла під кутом ₁ = 60 до                                                   F F_тр                      ^

горизонту, то тіло рухається рівномірно. З яким                                          x                   mg Мал. 13 прискоренням а рухатиметься тіло, якщо цю ж силу  прикласти під кутом ₂ = 30 до горизонту?

Розв’язання. Сили, що діють на тіло, показані на мал. 13. Запишемо їх проекції на осі х і у:

вісь х:	ma = F cos - Fтр	(1)
вісь у:	N = mg - F sin	(2)

сила тертя F_тр = kN, де k - коефіцієнт тертя. Коли сила прикладена під кутом 60 до горизонту, то рух рівномірний (а = 0). З цієї умови визначимо коефіцієнт тертя .

З рівнянь (1) і (2) враховуючи вираз для сили тертя отримуємо вираз для прискореного руху під дією сили, прикладеної під кутом ₂ і обчислимо результат:

F cos2  k(mg  F sin2) 2 a   0,9(м / с ).

m

Відповідь: а = 0,9 м/с².

Приклад 20. Кулька маси m₁, яка рухається з швидкістю v, абсолютно пружньо вдаряється об нерухому кульку маси m₂. При яких співвідношеннях мас m₁ i m₂ кульки після удару розлетяться з однаковими швидкостями? 

Розв’язання. Запишемо закон збереження імпульсу і закон збереження механічної енергії: m, де v₁ i v₂ швидкості

кульок після удару. Перетворимо вирази:

 m₁(v + v₁)(v  v₁) = m₂v₂²,  (1)  m₁(v + v₁) = m₂v₂. (2)

                 Розділивши (1) на (2), отримаємо: v  v₁ = v₂.                                      (3)

За умовою задачі: v₁ = v₂. Тому з (3): v₁ = v₂ = 0,5v. 

Підставимо це значення в (2) і отримаємо:  

 

Приклад 21. Потрібно викопати криницю глибиною Н = 12 м. На якій глибині h буде виконано половину всієї роботи? Густину ґрунту вважати сталою. Вийнятий ґрунт розсипають тонким шаром по землі.

Розв’язання. Робота по копанню криниці зводиться до зміни потенціальної енергії ґрунту, що виймається. Потенціальна енергія в полі сил тяжіння визначається з формули: Е_п = mgh. Бачимо, що ця енергія лінійно зростає із збільшенням h. Оскільки густина ґрунту стала, то вся робота по копанню криниці визначиться зміною потенціальної енергії центра ваги ґрунту,

що виймається. Тому: E .                                                                      (1)

Коли буде виконано половину роботи, то E,  (2) де m₁ - маса ґрунту, що буде вийнята у цьому випадку.

Вважаємо, що криниця має форму циліндра сталого перерізу S. Тоді маси m i m₁ будуть: m = V = SH, m₁ = V₁ = Sh.

Підставимо ці значення у вирази (1) і (2) і враховуючи, що Е = 2Е₁,



маємо: . 

Звідки: (м)

Відповідь: h = 8,57 м.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Нижчий рівень

1.61. Чи можуть дві сили, кожна з яких рівна 3 Н, мати рівнодійну 5 Н? Відповідь обґрунтуйте розрахунком і побудовою.

1.62. Дві сили величиною 20 Н і 30 Н прикладені до однієї точки тіла, утворюють кут 60. Визначити зрівноважувальну силу побудовою і розрахунком. 

1.63. Дві сили по 6 Н кожна прикладені до однієї точки тіла зрівноважуються силою 9 Н. Знайдіть кут між силами розрахунком і побудовою.

1.64. Три сили величиною 10, 12 і 10 Н діють в одній площині на точку тіла під кутами 120 одна до одної. Чому рівна рівнодійна цих сил?

1.65. При аварійному гальмуванні шлях автомобіля до зупинки дорівнює 12 м. Визначити початкову швидкість руху, якщо коефіцієнт тертя 0,6. 

1.66. Після поштовху вагон зупинився, проїхавши по горизонталі 37,5 м за 50 с. Визначити початкову швидкість і коефіцієнт тертя.

1.67. Тіло вагою 2000 Н рівномірно тягнуть по похилій площині, яка утворює кут 30 з горизонтом. До тіла прикладають силу 1500 Н. Чи рухатиметься тіло по похилій площині вниз, якщо його відпустити?

1.68. По похилій площині висотою 2 м і довжиною 6 м рухається вниз рівноприскорено вантаж. Яке прискорення руху, якщо коефіцієнт тертя 0,3?

1.69. Санки масою 75 кг, з’їжджаючи з гори, набули швидкості 5 м/с. Рухаючись далі по горизонтальному шляху, вони зупинились через 15 с.

Визначити коефіцієнт і силу тертя. 

1.70. Тролейбус, що почав рухатись, на шляху 50 м набув швидкості       10 м/с. Сила тяги двигуна дорівнює 14 кН, а коефіцієнт опору 0,004. Визначити масу тролейбуса. 

Оптимальний рівень 

1.71. Мішок з мукою сповзає без початкової швидкості з висоти 6 м по гладенькій дошці, нахиленій під кутом 60 до горизонту. Після спуску мішок потрапляє на горизонтальну підлогу. Коефіцієнт тертя мішка об підлогу 0,7.

Який шлях до зупинки пройде мішок по підлозі?

1.72. Санки вагою 60 Н скочуються з гори, нахиленої під кутом 30 до горизонту. Пройшовши по схилу 40 м, санки розвивають швидкість 3,6 м/с. Яка кількість тепла виділяється за рахунок тертя? 

1.73. Через нерухомий блок перекинуто нитку, до кінців якої підвішені важки по 0,24 кг. На один з важків поклали додатковий вантаж 0,01 кг. На якій відстані будуть один від одного важки через 2 с, якщо на початку руху вони були на однаковій висоті? Яка сила натягу нитки? 

1.74. Два вантажі масами 2 і 3 кг зв’язані ниткою і лежать на столі. До вантажу 3 кг приклали горизонтальну силу 15 Н. Визначити прискорення вантажів і силу натягу нитки між ними. Коефіцієнт тертя вантажів по поверхні столу 0,1. 

1.75. У кабіні ліфта до динамометра підвішено вантаж масою 1 кг. На початку піднімання ліфта динамометр показував 10,8 Н. Яким було прискорення ліфта в цей момент? 

1.76. Космічний корабель поблизу поверхні Землі рухається вертикально вгору з прискоренням 40 м/с². З якою силою космонавт тисне на сидіння, якщо вага космонавта 700 Н? 

1.77. Два вантажі масами 5 і 3 кг підвішені до кінців нитки, перекинутої через блок. Вантаж меншої маси знаходиться на 1 м нижче вантажу більшої маси. Вантажі починають рухатись під дією сили тяжіння. Нехтуючи тертям визначіть, через який час вони будуть на однаковій висоті? 

1.78. Визначити силу тяги двигуна автомобіля, який рухається вгору з прискоренням 1 м/с². Схил гори складає 1 м на кожних 20 м шляху. Маса автомобіля 900 кг, коефіцієнт тертя 0,1. 

1.79. На горизонтальній поверхні обертається кулька на дротині довжиною 0,6 м. З якою кутовою швидкістю обертається кулька, якщо сила натягу дротини в 2 рази більша за вагу кульки? 

1.80. Вантаж масою 0,5 кг, підвішений на дротині довжиною 0,6 м, коливаючись у вертикальній площині, проходить положення рівноваги з кутовою швидкістю 5 с^-1. Знайти силу натягу дротини.  Вищий рівень

1.81. Свинцева куля, яка летить з швидкістю v₁ = 400 м/с, пробиває дошку, внаслідок чого її швидкість зменшується до v₂ = 200 м/с. Температура кулі в момент удару 30 С. Яка частина кулі розплавиться, якщо на нагрівання витрачається 80% енергії? 

1.82. Кулька висить на легкій нерозтяжній нитці довжиною 1 м. Яку найменшу швидкість слід надати кульці в нижній точці, щоб вони зробила повний оберт у вертикальній площині? 

1.83. Визначити коефіцієнт тертя при русі тіла по похилій площині, якщо швидкість рівномірного руху вгору в 2 рази менша швидкості рівномірного руху вниз. В обох випадках затрачається однакова потужність. Площина нахилена під кутом 5 до горизонту. 

1.84. Вантаж масою 100 кг рухають рівномірно по горизонтальній площині, приклавши силу під кутом 30 до горизонту. Визначити величину цієї сили, якщо коефіцієнт тертя 0,3.

1.85. Льодяна гора нахилена під кутом 10 до горизонту. По ній знизу вгору пускають камінь, який за час 3 с проходить відстань 12 м, після чого починає рухатись вниз. Визначити час зворотнього руху каменя та коефіцієнт тертя між горою і каменем. 

1.86. Визначити роботу підняття вантажу масою 100 кг з прискоренням    1 м/с² по похилій площині довжиною 1 м нахиленій під кутом 30 до горизонту. Коефіцієнт тертя 0,1. 

1.87. Ковзаняр, стоячи на льоду, кинув вперед гирю масою 5 кг внаслідок чого поїхав назад з швидкістю 1 м/с. Маса ковзаняра 60 кг. Визначити роботу, яку він виконав при киданні гирі. 

1.88. Трамвай масою 19,6 т рухається рівномірно з швидкістю 32,4 км/год по опуклому мосту, що має радіус кривизни 30 м. З якою силою тисне трамвай на міст на відстані 15,7 м від його середини?

1.89. Люстра вагою 680 Н підвішена до стелі металевим ланцюгом, довжина якого 3 м. На який найбільший кут можна її відхиляти при ремонті, щоб при випадкових вільних коливаннях люстри ланцюг не розірвався? Розрив ланцюга настає при натягу 1360 Н.

Якісні завдання

1.90. Під дією сталої сили 10 Н тіло рухається прямолінійно так, що залежність координати від часу дається рівнянням х = 10t + t². Зобразити на графіках: а) залежність швидкості руху від часу; б) зміну з часом кінетичної енергії тіла.

1.91. Автомобіль маси m з вимкненим двигуном скочується з гори висотою h і довжиною L зі сталою швидкістю на горизонтальну ділянку дороги. Коефіцієнт тертя на обох ділянках руху рівний . Накреслити графік шляху, пройденого автомобілем до зупинки.

1.92. Тіло вільно падає з деякої висоти. Яким буде його переміщення за  n–ту секунду після початку падіння?

1.93. Тіло кинули горизонтально з деякої висоти. Як зміниться час і далекість польоту, якщо швидкість кидання збільшити вдвічі?

1.94. Як можна порівняти маси тіл в космічному кораблі при його вільному польоті?

1.95. Чому великі краплі дощу падають з більшою швидкістю, ніж дрібні?

1.96. Похила площина розташована під кутом  до горизонту. При яких значеннях коефіцієнта тертя витягувати по ній вантаж важче, ніж піднімати його вертикально?

1.97. Що легше: тягнути санки, чи штовхати їх? Чому?

1.98. Чому людина, яка несе на спині важкий вантаж, нахиляється трохи вперед?

1.99. Оцініть найменшу і найбільшу силу, яка необхідна для перекидання коробки сірників. Чи завжди її можна перекинути?

1.100. Дерев’яна дошка має довжину 5 м і масу 10 кг. Яку силу потрібно прикласти, щоб один її кінець відірвати від землі?

          

1.4. КОЛИВАННЯ І ХВИЛІ

В природі зустрічаються рухи, які повністю повторюються в часі. Такі рухи називаються періодичними. Системи, в яких можуть відбуватись періодичні рухи, називаються коливальними.

Найпростіші періодичні коливання, що здійснюються під дією сили, величина якої пропорційна зміщенню від положення рівноваги, називаються гармонічними коливаннями. Прикладами таких коливань можуть бути: коливання математичного маятника; коливання тіла, підвішеного на пружині і т.д. (без врахування втрат енергії на тертя і опір середовища). Рівняння гармонічного коливного руху має вигляд:

                                      x ),       (1.52)

                 або               x  

де: х - зміщення точки від положення рівноваги в довільний момент часу t; А - амплітуда (найбільше відхилення від положення рівноваги); Т - період коливань;  - початкова фаза (величина, що показує, яка доля періоду минула від початку коливань);  - частота коливань;  = ^ – кутова частота.

Швидкість точки, яка здійснює гармонічні коливання:

                                                     v ),                           (1.54)

прискорення:                        a ).                        (1.55)

Сила, під дією якої точка маси m здійснює гармонічні коливання, рівна

                                             F - kx  (1.56)

Період коливання: 

математичного маятника  ^{T  2} (1.57) пружинного маятника  ^{T  2} (1.58)

Кінетична енергія коливної точки:

                                                   W_k )                   (1.59)

Потенціальна енергія: 

                                                   W_п )                    (1.60)

                 Повна енергія:                    W ).                                        (1.61)

Реальні коливання завжди будуть згасаючими через втрату частини енергії на подолання сил тертя і опору середовища. Щоб підтримувати коливання сталими, до системи потрібно підводити енергію, яка б компенсувала втрати. У тому випадку, коли частота зміни зовнішньої сили співпадає з частотою власних коливань системи, настає явище резонансу – різкого зростання амплітуди коливань системи. Це явище має як корисну, так і шкідливу дію.

Тіло, що коливається, захоплює в цей процес частки оточуючого його середовища, що приводить до поширення коливань у просторі, тобто до появи хвиль.

Хвилі можуть бути як поздовжніми – напрям поширення хвилі співпадає з напрямом коливань системи, так і поперечними – хвиля поширюється в напрямку, перпендикулярному до напряму коливань системи.

Відстань, на яку поширюється хвиля за час одного періоду коливань, називається довжиною хвилі (). Це також буде відстань між двома сусідніми точками середовища, які коливаються в однаковій фазі.

              Швидкість поширення коливань v ^ .                                  (1.62)

 

Приклади розв’язання задач

Приклад 22. Матеріальна точка здійснює гармонічні коливання з частотою 500 Гц і амплітудою 0,02 см. Визначити середні значення швидкості і прискорення точки на шляху від її крайнього положення до положення рівноваги. Знайти також максимальні значення цих величин.

Розв’язування. За означенням середня швидкість v_c = ^, де: L - шлях,



пройдений точкою за час t. В нашому випадку L = А =2·10^-4 м, t , тому що за час періоду Т точка проходить шлях, що дорівнює чотирьом амплітудам.

Тому маємо, що v_c  Гц=0,4 (м/c).

З формули (1.54), прийнявши 1, знаходимо максимальну швидкість v.

За означенням середнього прискорення запишемо: a_с ^ , де v = v - v_o. У

нашому випадку v_o = 0, кінцева швидкість v = v_max = 0,63 (м/c), t .



Маємо: a_c  



З формули (1.55), прийнявши 1, знаходимо максимальне прискорення: a_max = 4_²_²A = 4·3,14²·500²·2·10^-4 = 2·10³ (м/c²).

Відповідь: v_c = 0,4 м/c, v_max = 0,63 м/c, a_c = 1,2·10³ м/c², a_max = 2·10³ м/c².

Приклад 23. За який час точка, що здійснює гармонічні коливання з періодом 12 с, пройде шлях, рівний: 1) половині амплітуди, якщо у початковий момент вона була в положенні рівноваги; 2) третині амплітуди, якщо у початковий момент вона перебувала у крайньому положенні?

Розв’язання. Шлях L(мал. 14) знаходимо з рівняння гармонічних коливань:

                                                       x ].                                         (1)

Щоб знайти початкову фазу, скористаємось початковими умовами задачі: х = 0 при t = 0.

Підставивши ці значення в (1), маємо  = 0. Тоді: 

                                                           x )                                                (2)

Оскільки x , або .

                    Звідси: t 1 c. Позначимо його t₁.

2) Точка рухається з крайнього положення, тому початкові умови будуть такі: х = А при t = 0. Підставивши це значення в (1), маємо, що  = ^. Тоді:

                                                 x )                                (3)

Щоб не допустити помилки, врахуємо, що величина х показує зміщення точки від положення рівноваги (точки О на мал. 14), а не шлях, пройдений нею. Якщо точка рухалась з крайнього положення і пройшла шлях, рівний третині амплітуди, то x .

Підставивши це значення в (3), маємо . Користуючись

 таблицями косинусів, знаходимо, що .

Звідки: t . Це і буде значення t₂.

Відповідь: t₁ = 1 c, t₂ = 1,6 c. 

Приклад 24. Вантаж вагою 0,5 Н, підвішений на нитці, відвели вбік так, що кут між ниткою і вертикаллю складає 12. Знайти: 1) силу, що повертає тіло до положення рівноваги; 2) силу натягу нитки; 3) прискорення, з яким рухатиметься вантаж, якщо його відпустити. 

Розв’язання. На вантаж діє сила тяжіння, яка рівна його вазі Р. Оскільки нитка відхилена від вертикалі на кут , то дія цієї сили приводить до появи двох сил (мал. 15): сили F₁, яка намагається повернути тіло в положення рівноваги, і сили F₂, яка розтягує нитку. З малюнка маємо, що: 

F₁ = Psin; F₂ = Pcos.

Обчислимо: F₁ = 0,5·0,208 = 0,104 (H). F₂ = F_н = 0,5·0,987 = 0,489 (H).

Сила F₁ буде повертати тіло до положення рівноваги. За другим законом

Ньютона: а  

Відповідь: F₁ = 0,104 H, F_н = 0,489 H, a = 2,04 м/c².

Приклад 25. Хвиля, створена катером, що рухається на відстані S = 200 м від берега, дійшла до берега через час t = 90 с. Яка довжина хвилі , якщо частота ударів хвиль об берег  = 0,5 Гц?

Розв’язання. У пружних середовищах хвилі поширюються рівномірно, тому швидкість поширення хвиль у воді визначиться як: v .

Довжина хвилі – це відстань, на яку поширюється хвиля за час одного періоду коливань:  .

Відповідь:  = 4,44 м.

 

ЗАДАЧІ ДЛЯ САМОСТІЙНОЇ РОБОТИ

1.101. Космічний корабель рухається з прискоренням а. Як за коливанням математичного маятника в його кабіні визначити це прискорення?

1.102. Як зміниться хід маятникового годинника, якщо його перевезти з Одеси у Київ?

1.103. Пружинний маятник здійснює гармонічні коливання з амплітудою 6 см. Визначити зміщення кульки через час 5,2·10^-2 с від початку коливань, якщо початкова фаза рівна нулю. Маса кульки 15 г, жорсткість пружини          15 Н/м.

1.104. Математичний маятник довжиною 1 м підвішений у вагоні рухомого поїзда. При якій швидкості руху поїзда маятник відхилятиметься на найбільший кут? Довжина рейок 12,5 м.

1.105. Амплітуда гармонічних коливань 50 мм, період 4 с, а початкова фаза  ^. Записати рівняння коливань та побудувати його графік.

1.106. Тіло здійснює гармонічні коливання. Яким буде відношення його кінетичної енергії до потенціальної у той момент часу, коли зміщення від положення рівноваги складає четверту частину амплітуди?

1.107. Амплітуда гармонічних коливань точки масою 50 г рівна 2 см, а повна енергія 3·10⁷ Дж. Яка частота коливань точки? 

1.108. Звукові коливання частотою 500 Гц поширюються у повітрі, маючи довжину 70 см. Знайти швидкість звуку у повітрі.

1.109. Хвиля поширюється з швидкістю 2,4 м/с. Яка різниця фаз двох точок, віддалених між собою на 20 см, якщо частота коливань 3 Гц?

1.110. Мідна кулька, підвішена на пружині, здійснює гармонічні коливання. Як зміниться період коливань, якщо до пружини підвісити алюмінієву кульку такого ж радіуса? Густина міді ₁, алюмінію ₂.

          

2. МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА

                 Кількість речовини (в молях) дорівнює ,                           (2.1)

де      N       -        кількість     молекул      в        даному       тілі,   N_A     -        стала          Авогадро,                 N_A = 6,02·10²³ моль^-1, m - маса тіла, M - молярна маса речовини. Маса молекули

m.                                                                                                          (2.2)

Основне рівняння молекулярно-кінетичної теорії газів: 

                                                       p ,                                           (2.3)

де р - тиск, n - кількість молекул в одиниці об’єму, E - середня кінетична енергія поступального руху молекул, v² - середня величина квадрата швидкості поступального           руху молекули.   Ці      величини    зв’язані       з        абсолютною

температурою Т такими співвідношеннями: E kТ;    (2.4)   v,      (2.5)

де k - стала Больцмана, k = 1,38·10^-23 Дж/К, R = kN_A – універсальна газова стала, R = 8,31 Дж/(Кмоль) = 8,31·10³ Дж/(кмоль К).

Рівняння стану ідеального газу (рівняння Менделеєва-Клапейрона):

          pV RT,  (2.6) де V - об’єм посудини, в якій знаходиться газ.

З рівняння стану для сталої маси ідеального газу витікають такі закони:

1)   Бойля-Маріота T = const. PV =const, або P₁V₁ = P₂V₂.        (2.7)

2)   Гей-Люссака P = const.  const, або .          (2.8)

3)   Шарля V = const. const, або .           (2.9) 

                 Перший закон термодинаміки: U = Q - A,                                      (2.10)

де: U - зміна внутрішньої енергії системи, Q - кількість теплоти, A - робота, яку виконала система в процесі.

Для ізобарного процесу (p = const) розширення системи

                                                               A = p(V₂ - V₁).                                       (2.11)

Внутрішня енергія U одноатомного ідеального газу дорівнює

                                                              U RT.                                           (2.12)

При нагріванні тіла від температури Т₁ до температури Т₂, якщо не відбувається процесів плавлення, кристалізації, випаровування та конденсації, треба надати йому кількість теплоти 

                                               Q = C(T₂ - T₁), або Q = cm(T₂ - T₁),                      (2.13)

де: С - теплоємність тіла, c - питома теплоємність речовини, m - маса тіла. Якщо тіло охолоджується від температури T₂ до температури T₁, то відповідна кількість теплоти виділяється.

Якщо тверде тіло перетворюється в рідину при Т = const, то воно поглинає кількість теплоти: Q = m, де  - питома теплота плавлення. Якщо рідина перетворюється в тверде тіло при Т = const, то така ж кількість теплоти виділяється.

Коефіцієнт корисної дії (ККД) теплового двигуна дорівнює:

                                                     100%,                          (2.14)

де Q₁ - кількість теплоти, яку взято робочим тілом від нагрівника, Q₂ - кількість теплоти, яку віддає робоче тіло холодильнику, А - виконана робота. Максимальне значення ККД _max має так звана ідеальна теплова машина:      , де Т₁ - абсолютна температура нагрівника, а Т₂ - абсолютна

температура холодильника.

                 Закон Гука:                         E|L|L₀,                                           (2.15)

де F - сила, що розтягує стержень з площиною перерізу S. L = L - L₀ - видовження стержня, що мав до дії сили довжину L₀, Е - модуль Юнга

речовини. Величина  зветься механічною напругою.

Коефіцієнт поверхневого натягу в рідині визначається за формулою

                                                                ,                                                 (2.16)

де А - робота, необхідна для збільшення площі поверхні рідини на величину S.

Висота h підняття рідини з густиною , що повністю змочує капіляр з

радіусом r дорівнює                         h = ^.                                                  (2.17)



Відносна вологість повітря f визначається за формулою

                                                             f 100%,                                    (2.18)

де P(T) - тиск водяної пари, що знаходиться у повітрі при температурі Т,   P_нас(T) - тиск насиченої водяної пари при температурі Т.

Точка роси - це така температура, при якій водяна пара, що знаходиться у повітрі стає насиченою.

 

Приклади розв’язання задач

Приклад 26. Під час ізохоричного охолодження тиск газу зменшився на 100 кПа. Визначити початковий тиск, якщо абсолютна температура газу зменшилась у 1,5 рази.

Розв’язання. Із закону Шарля для ізохорного процесу 

                                                                 = 1,5                                            (1)

де: р₁ – початковий, а р₂ – кінцевий тиск газу. За умовою задачі                р₁ - р₂=100 (кПа). Тому:          = 1,5.         (2)

Звідси: р₁ = 1,5р₁ - 150, або 0,5р₁ = 150. р₁ = 300 (кПа).

Відповідь: р₁ = 300 кПа.

Приклад 27. Скільки льоду, взятого при t₁ = 0 С потрібно для охолодження 4,5 л води від t₂ = 30 С до t₃ = 10 C? Питомі теплоємності: води с₁ = 4200 Дж/кг К, льоду с₂ = 2100 Дж/кг К, питома теплота плавлення льоду      = 330000 Дж/кг, густина води  = 1000 кг/м³.

Розв’язання: При охолодженні від t₂ до t₃ вода віддасть Q₁ теплоти. Вона піде на плавлення льоду Q₂ і на нагрівання води, що утворилась з розплавленого льоду Q₃. За законом збереження енергії запишемо рівняння теплового балансу: Q₁ = Q₂ + Q₃. Q₁ = c₁m₁(t₂ - t₃); Q₂=m₂; Q₃ = c₂m₂(t₃ - t₁).

Маса води m₁ = V, де:  - густина води, V – її об’єм. Запишемо рівняння теплового балансу з урахуванням виразів для кількості теплоти: c₁m₁(t₂ - t₃) = m₂ + c₂m₂(t₃ - t₁).

Звідси: m.

                    Обчислимо: m = 1 кг.

Відповідь: потрібно взяти 1 кг льоду.

Приклад 28. Балон ємкістю 40 л містить 1,97 кг вуглекислого газу (СО₂). Балон витримує тиск не більший 3,039·10⁶ Н/м². При якій температурі виникне загроза вибуху?

Розв’язання: Для сталої маси m газу, що має молярну масу М, його тиск Р, об’єм V і температура Т пов’язані рівнянням Менделеєва-Клапейрона:       

PV RT, де: R = 8,32·10³ (Дж/кмоль) К – універсальна газова стала.

Для розрахунку критичної температури вважатимемо, що тиск у балоні повинен досягти максимально можливого, який ще витримує балон. Тому:     

T_кр . 

Врахуємо, що для СО₂ М = 12 + 16·2 = 44 (кг/кмоль), V = 40·10^-3 (м³).

Обчислимо: Т_кр .

Відповідь: Т_кр = 327,6 К = 54,6 С.

Приклад 29. Який тиск на стінки посудини чинить кисень, якщо середня квадратична швидкість його молекул 400 м/с, а кількість молекул в 1 см³ дорівнює 2,7·10¹⁹?

Розв’язання: Тиск в посудині створюється передачею імпульсу молекул кисню при їх зіткненні зі стінками. Основне рівняння молекулярно-кінетичної теорії ідеального газу можна записати: p ; де: n - концентрація молекул, m_o - маса молекули кисню, v_c² - середня квадратична швидкість, М – молярна маса кисню (M = 32 кг/кмоль), N_А = 6,02·10²⁶ (кмоль^-1) – число

Авогадро. 

В одиницях СІ n = 2,7·10¹⁹ см^-3 = 2,7·10²⁸ (м^-3). Обчислимо: p .

Відповідь: р = 7,6·10⁴ Па.

Приклад 30. Яку швидкість повинна мати свинцева куля, щоб при ударі у сталеву плиту вона розплавилась? Температура кулі до удару t_o = 27 С, температура плавлення свинцю t₁ = 327 С, питома теплота плавлення свинцю   = 25·10³ Дж/кг, питома теплоємність свиню c = 0,13·10³ Дж/кг К.

Розв’язання. Рухаючись зі швидкістю v, куля маси m має кінетичну енергію Е_к . Свинець відноситься до пластичних металів, тому удар кулі зі стальною плитою можна вважати абсолютно непружнім. При цьому вся кінетична енергія кулі перейде в теплову і приведе до нагрівання кулі до температури плавлення свинцю і її плавлення. Закон збереження енергії (рівняння теплового балансу) матиме вигляд: ) + m.

_{Звідки:} v  2c(t₁  t₀)  320(м / c).

Відповідь: куля повинна мати швидкість 320 м/c.

Приклад 31. В циліндричній посудині під поршнем, що легко рухається, знаходиться 1 моль ідеального одноатомного газу при температурі Т₁ = 300 К.

Яку кількість теплоти потрібно надати газу, щоб його об’єм збільшити в 3 рази. Розв’язання. Запишемо перше начало термодинаміки:

Q  

Так, як поршень рухається легко, то процес можна вважати ізобаричним, звідки маємо, що 3. Тобто Т₂ = 3Т₁.

Для одного моля газу рівняння Менделеєва-Клапейрона: pV = RT.

Враховуючи це, маємо: Q = 5RT₁ = 12,5·10³ (Дж).

Відповідь: газу потрібно передати 12,5·10³ Дж теплоти.

Приклад 32. Визначити густину суміші, яка складається з кисню m₁ = 50 г та водню m₂ = 20 г при температурі 300 К і тиску 1 МПа.

Розв’язання. В посудині знаходиться два гази, які разом створюють тиск

р. Цей тиск обумовлений парціальними тисками кисню р₁ і водню р₂, причому  р = р₁ + р₂. З рівняння Менделеєва-Клапейрона для кожного з газів:

pRT; pRT,

де: М₁ і М₂ – молярні маси кисню і водню відповідно, R - універсальна газова стала. Для суміші газів: pV .

Густина суміші:  .

Числові значення: m₁ = 5·10^-2 (кг), m₂ = 2·10^-2 (кг), M₁ = 32 (кг/кмоль),              M₂ = 2 (кг/кмоль). Обчислення дають значення  = 0,23 (кг/м³).

Відповідь: густина суміші 0,23 кг/м³.

Приклад 33. Діаграма циклічного процесу для одного молю ідеального газу в координатах p і Т утворює прямокутник (мал. 16). Знайти найменший та найбільший об’єми газу.  

Розв’язання. Мінімальний об’єм газу відповідає точці (Т₁,

р₂) і дорівнює V. Максимальний об’єм відповідає точці

(Т₂, р₁) і буде рівний V.

.

Приклад 34. Яку кількість теплоти віддає 1 моль одноатомного ідеального газу при його ізобарному охолодженні від температури Т₁ до температури Т₂, якщо на стискання газу затрачено роботу 12 Дж?

Розв’язання. З першого закону термодинаміки маємо: U = Q - A, де U - зменшення внутрішньої енергії, Q - передана кількість теплоти, А - виконана робота. Для одноатомного ідеального газу:

U  

Тоді: Q .

Відповідь: Q = 30 Дж.

Приклад 35. Яку роботу треба виконати, щоб краплю води радіусом 1 мм розділити на 1 мільйон маленьких крапельок? Коефіцієнт поверхневого натягу води  = 7,3·10^-2 Н/м.

Розв’язання. При розділенні краплі утворюється нова поверхня. Треба знайти збільшення площі цієї поверхні. Оскільки крапля розділяється на мільйон окремих крапель, то V = 10⁶V₁, де V – об’єм великої краплини, V₁ – об’єм малої краплини. Радіуси краплин будуть: R = 100R₁, де: R - радіус великої, а R₁ - радіус малої краплини. Площа поверхні великої краплини:          

S = 4R², а малої відповідно S₁ = 4R₁² = 10^-4·4R².

Загальне збільшення площі: S = 10⁶S₁ – S = 4R²(100 - 1)=396R².

Тоді робота, затрачена на розділення краплі:

A = S =7,3·10^-2·396·3,14·10^-6 = 9,1·10^-5 (Дж).

Відповідь: А = 9,1·10^-5 Дж.

Приклад 36. Абсолютне й відносне видовження стержня становить відповідно 1 мм і 0,1%. Яку довжину мав недеформований стержень?

Розв’язання. Абсолютне видовження стержня L = L - L_o, де L – кінцева і L_o – початкові довжини стержня. Відносне видовження х ^ 100%. 

Тоді: L_o .

Відповідь: недеформований стержень мав довжину 1 м.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Вищий рівень 

2.1. Із посудини об’ємом V, тиск в якій дорівнює Р₁, відкачують повітря. Скільки качань повинен зробити поршневий насос об’ємом V_o для того, щоб тиск в посудині зменшився в k разів? Температура повітря не змінюється.

2.2. В посудині знаходиться повітря при температурі 10 С з відносною вологістю 60%. Густина насиченої пари при цій температурі становить   9,43·10^-3 кг/м³. Якою буде відносна вологість цього повітря, якщо його підігріти до температури 100 С і зменшити об’єм в 3 рази? Густина насиченої пари при 100 С становить 0,6 кг/м³.

2.3. Деяку кількість ідеального газу нагріли при постійному тиску 10⁴ Па від температури 300 К до температури 400 К. Яку роботу виконує газ у цьому процесі, якщо його початковий об’єм 30 л?

2.4. Два молі ідеального одноатомного газу розширюються без теплообміну з навколишнім середовищем. Температура газу при розширенні зменшилась на 10 К. Визначити роботу, що її здійснює газ при розширенні.

2.5. Підрахувати питомі теплоємності при постійному об’ємі і при постійному тиску для аргону (М = 4·10^-2 кг/моль).

2.6. На якій глибині бульбашка повітря, що підіймається у воді, матиме у 2 рази менший об’єм, ніж на поверхні? Зовнішній тиск нормальний. 

2.7. До якої температури треба ізобарично нагріти газ, щоб його густина зменшилась вдвічі порівняно з густиною при 0 С? 

2.8. При збільшенні абсолютної температури ідеального газу вдвічі його тиск збільшився на 25%. У скільки разів змінився об’єм газу?

2.9. Суміш з свинцевих та алюмінієвих ошурок загальною масою 150 г і температурою 100 С висипали в посудину, що містить 230 г  води при температурі 15 С. При цьому вода нагрілась до 20 С. Скільки свинцю та алюмінію було в суміші? Теплоємністю посудини знехтувати. 

2.10. У балоні міститься газ при температурі 15 С. У скільки разів зменшиться тиск газу, якщо 40% його вийде з балона, а температура при цьому понизиться на 8 С?

2.11. З деякою масою ідеального газу виконали коловий процес, зображений на мал. 17. Пояснити, як змінювався об’єм газу в процесі переходів 1-2, 2-3, 3-4, 4-1.  

2.12. Визначити ККД газового пальника, якщо в ньому використовується газ, теплота згоряння якого 3,6·10⁷ Дж/м³, а на нагрівання залізного чайника масою 0,75 кг з 3 л води від 10 С до кипіння було витрачено 60 л газу.

2.13. Об’єм 160 г кисню, температура якого 27 С, внаслідок ізобарного нагрівання збільшився вдвічі. Визначити роботу газу під час розширення, кількість теплоти, яка пішла на нагрівання кисню, і зміну внутрішньої енергії. 

2.14. Кристали кухонної солі NaCl мають кубічну структуру і складаються з іонів Na⁺ i Cl^-, які чергуються в кристалі. Визначити середню відстань між центрами іонів, якщо густина солі 2200 кг/м³.

2.15. Середня квадратична швидкість молекул газу при тиску 2·10⁵ Па становить 600 м/с. Визначити густину газу за цих умов. 

2.16. Для одержання дистильованої води використовується електронагрівник, що має ККД 90%. Яка собівартість перегонки 1 кг води, якщо вона надходить у нагрівник, маючи температуру 15 С? Тариф: 167 коп. за 1 кВт·год.

2.17. У капілярній трубці, радіус якої 0,5 мм, рідина піднялась на висоту 11 мм. Визначити густину цієї рідини, якщо її коефіцієнт поверхневого натягу 0,022 Н/м.

Оптимальний рівень

2.18. Газ під тиском 0,2 МПа і при температурі 15 С займає об’єм 5 л. Яким буде об’єм цієї маси газу за нормальних умов? 

2.19. У скільки разів і як зміниться густина ідеального газу при пониженні температури від 127 до 7 С, якщо тиск залишиться сталим? 

2.20. До якої температури було нагріто деяку масу ідеального газу, якщо під час нагрівання її на один градус тиск зріс на 1/400 частину початкового тиску? Процес ізохорний. 

2.21. Азот і водень при однаковій температурі мають однакові густини. Як відносяться їх тиски? 

2.22. Згинаючи багато разів алюмінієву дротину масою 2 г, її нагріли на 40. Яка при цьому виконана робота, якщо лише 30% її йде на нагрівання дротини? 

2.23. Температура нагрівника ідеальної теплової машини 117 С, а холодильника 27 С. Кількість теплоти, яку дістає машина від нагрівника за 1 с, дорівнює 60 кДж. Обчисліть ККД машини, кількість теплоти, яку забирає холодильник за 1 с, і потужність машини. 

2.24. Яка енергія поступального руху молекул 10 мг водню при температурі 100 С?

2.25. Який об’єм займає газ при температурі 12 С і під тиском 200 кПа, якщо число молекул газу становить 5,4·10²⁶?

2.26. У посудину, що містить 1,5 кг води при температурі 15 С, впустили

200 г водяної пари при температурі 100 С. Яка температура встановилась в посудині після конденсації пари?

2.27. На яку висоту підніметься вода при температурі 18 С у скляній капілярній трубці, що має діаметр 2 мм? 

2.28. У посудину, яка містить 10 кг льоду при температурі 0 С, влили     

3                    кг води при температурі 90 С. Яка температура встановиться в посудині? Чи розплавиться весь лід? Теплоємності посудини не враховувати. 

2.29.      При температурі 0 С алюмінієва лінійка має довжину 79,5 см, а стальна 80 см. При якій температурі обидві лінійки матимуть однакову довжину? 

2.30.      Стальна деталь, нагріта під час обробки до 800 С, має розміри 1,2×0,75×0,4 мм. Які розміри вона матиме при температурі 20 С? 

Якісні завдання

2.31.      Як змінюється температура деякої маси ідеального газу, що розширюється за законом pV = const: А) підвищується; Б) не змінюється; В) зменшується.

2.32.      Чому дорівнює теплоємність 1 моля ідеального одноатомного газу в ізотермічному процесі?

А) R; Б) 0; В) нескінченна величина.

2.33.      За рахунок чого ідеальний газ при ізотермічному розширенні виконує роботу?

А) зменшення внутрішньої енергії; Б) підведення до газу певної кількості теплоти; В) (А + Б).

2.34.      Як змінюється внутрішня енергія ідеального газу при ізохоричному зменшенні тиску?

А) не змінюється; Б) зменшується; В) збільшується.

2.35.      Який ґрунт швидше нагрівається сонцем: вологий чи сухий?

2.36.      Коли вітрильним суднам зручніше входити в гавань – вдень чи вночі?

2.37.      Чи можна підвищити температуру тіла, не надаючи йому теплоти?

2.38.      Що легше: 1 м³ сухого повітря, чи 1 м³ вологого?

2.39.      Чому дерева іноді гинуть від морозу?

2.40.      Вогка білизна, яку вивісили взимку надворі замерзає. Через деякий час вона стає сухою навіть при сильних морозах. Чим це пояснити?

2.41.      Чому сирі дрова горять гірше, ніж сухі?

2.42.      Чому дорівнює максимальний ККД теплового двигуна, що працює з нагрівачем при температурі Т₁ та холодильником при температурі Т₂?

А) ; B) .

2.43.      Як залежить внутрішня енергія ідеального одноатомного газу від температури?

А) прямо пропорційно; Б) обернено пропорційно; В) не залежить.

2.44.      Деформація стержня називається пружною, коли:

А) його відносне видовження лінійно залежить від механічної напруги; Б) після зняття механічної напруги він відновлює свою довжину; В) його відносне видовження не залежить від механічної напруги.

          

3. ОСНОВИ ЕЛЕКТРОДИНАМІКИ

3.1. ЕЛЕКТРИЧНЕ ПОЛЕ

Електрична взаємодія двох точкових зарядів описується законом Кулона: сила взаємодії двох точкових зарядів q₁ і q₂, пропорційна величині зарядів, обернено пропорційна квадрату відстані r між ними і направлена вздовж прямої, що сполучає ці заряди: 

1 q¹  q²

                                                                                        F_K              ₂                                                 (3.1)

                                                                                                   4₀              r

де ₀ = 8,85·10^-12 Ф/м – діелектрична проникність вакууму (електрична стала).

Напруженістю електричного поля Е називається векторна величина, що показує, яка сила діє на одиничний електричний заряд, поміщений в дану точку

F

поля:                                                     E                     (3.2) q

                 Для точкового заряду            E           ₂                                           (3.3)

4₀ r

Якщо поле створене кількома зарядами, то результуюча напруженість визначається з принципу суперпозиції полів: загальна напруженість електричного поля, створеного системою зарядів, рівна геометричній сумі

                                                                                                                                        r       r

напруженостей, створених кожним з цих зарядів: EE_i                            (3.4)

Напруженість електричного поля у діелектрику зменшується в  разів порівняно з його напруженістю у вакуумі. Величина  називається відносною діелектричною проникністю. Зменшення напруженості поля в діелектрику обумовлена його поляризацією – появою зв’язаних зарядів на поверхні діелектрика.

Завдяки тому, що в металах є значна кількість вільних електронів, напруженість електричного поля всередині металів рівна нулю, що використовується для електростатичного захисту.

Потенціалом електричного поля  називається величина, що показує, яка потенціальна енергія W припадає на одиничний електричний заряд в даній

W

точці поля:                                                                                            (3.5)

q

Потенціальна енергія взаємодії двох точкових зарядів q₁ і q₂, що

перебувають на відстані r:                     W                                        (3.6)

                 Для точкового заряду                   W                                        (3.7)

Якщо поле створене кількома зарядами, то потенціал даної точки поля рівний алгебраїчній сумі потенціалів, створених окремими зарядами.

Робота, виконана силами поля по переміщенню заряду q із точки з потенціалом ₁ в точку з потенціалом ₂:

                                                                Aq(₁ ₂)= -W = qU                                 (3.8)

Електричне поле є потенціальним, тобто робота по переміщенню заряду не залежить від форми траєкторії, по якій переноситься заряд. 

Для однорідного поля зв’язок між потенціалом і напруженістю має

вигляд:                                   E ^                                          (3.9)

де L – відстань між двома точками поля, яка вимірюється вздовж силової лінії, U - напруга, або різниця потенціалів.

Електрична ємність конденсатора (двох ізольованих провідників) визначається відношенням заряду до різниці потенціалів:

                                                             C                                        (3.10)

           Для плоского конденсатора C= ^0S                                            (3.11)

L

де  - діелектрична проникність середовища, яке заповнює конденсатор, S - площа пластин конденсатора, L - відстань між ними.

Ємність батареї з n паралельно сполучених конденсаторів рівна сумі

ємностей всіх конденсаторів Спарал  Сi                                                                                     (3.12)

Ємність батареї послідовно сполучених конденсаторів визначається з

1                            1

формули Cпосл ^{ }_Ci                                                                                     (3.13)

Енергія електричного поля зарядженого конденсатора 

                                                                                             qU     CU ²             q²

                                                                 W                                                       (3.14)

2                            2         2C

 

Приклади розв’язування задач

Приклад 37. Порівняти сили електростатичної і гравітаційної взаємодії двох електронів.

Розв’язання. Сила електростатичної взаємодії електронів згідно з законом

Кулона: F_е  

                      Гравітаційна взаємодія описується             законом всесвітнього тяжіння:           

Fг  

де: q і m – заряд і маса електрона відповідно, r - відстань між електронами, _o - діелектрична проникність вакууму, G - гравітаційна стала.

Відношення сил взаємодії: .

Обчислимо: 

.

Відповідь: сила електростатичної взаємодії електронів перевищує силу гравітаційної взаємодії у 4,3·10⁴² рази.

Приклад 38. Дві однакових кульки масами m підвішені в одній точці на нитках довжиною L. Після того, як кулькам надали однакового заряду, вони розійшлись на кут . Знайти заряди кульок. 

Розв’язування: На кожну кульку (мал. 18) діють дві сили:

вага кульки Р = mg і сила електричного відштовхування              

F_е , де ^.

Тому F_e .

                 З малюнка бачимо, що F₁ ^.

Кулька перебуватиме в рівновазі, якщо модулі сил F_e i F₁ будуть однаковими, тобто F_e = F₁. Прирівняємо праві частини виразів для сил:

.

                                       q                                    mgtg  4L sin  mgtg         .

Звідси:

Це і буде відповідь.

Приклад 39. Дві однакові металеві кульки мають додатні заряди              q₁ = 1,67·10^-9 Кл і q₂ = 6,67·10^-9 Кл і розташовані на відстані r = 10 см одна від одної. Чи зміниться сила взаємодії кульок після того, як їх на мить з’єднати?

Який заряд буде на кожній кульці після цього?

Розв’язування. Знайдемо початкову силу взаємодії кульок.

F.

Так як заряди кульок однойменні, то після короткочасного з’єднання, вони розподіляться на однакові долі. Тоді на кожній кульці буде заряд  q'  

Знайдемо тепер значення сили взаємодії:

F'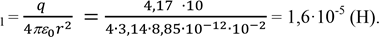

Відповідь: сила взаємодії збільшиться майже у півтора рази, на кожній кульці буде заряд 4,17·10^-9 Кл.

Приклад 40. Два однойменні заряди по q₁ = q₂ = 25 нКл, віддалені на         a = 24 см один від одного, створюють електростатичне поле. З якою силою це поле діє на заряд q = 2 нКл, розташований у точці, що перебуває на відстані      b = 15 см від кожного з зарядів?

Розв’язання. Сила, з якою електричне поле діє на заряд визначається з виразу:

                                                                F = qE                                                    (1)

де Е - напруженість поля в точці, де перебуває заряд. В точці, де поміщено заряд q електричне поле створюється зарядами q₁ і q₂. Згідно з принципом суперпозиції полів, результуюче поле рівне векторній сумі полів, створених

кожним із зарядів: E=E₁+E₂                                                                            (2)

Величини зарядів q₁ і q₂ однакові, відстані точки, де поміщається заряд q, від зарядів q₁ і q₂ теж однакові, тому модулі напруженостей Е₁= Е₂. З мал. 19 маємо:

                                                              E                                                (3)

Результуючу напруженість знайдемо за теоремою косинусів

                                                                                    2            2

                                                                       E  E₁ E₂  2E₁E₂ cos,                                     (4)

 

де  – кут між векторами Е₁ і Е₂. Величину цього кута знайдемо з таких міркувань. Трикутник АВС прямокутний. Кут при вершині В знайдемо як:   сosB 0,8. Тоді кут В = 3650'. Кут при вершині А рівний         



'. Значить  = 10620'.

З малюнка бачимо, що модулі напруженостей Е₁ і Е₂ однакові, тому формулу (4) можна переписати так: 

                               2             2

E                   2E₁  2E₁ cos  E₁ 2(1  cos)

 9

                                                     2(1  0,28)

4  3,14  8,85  10^12  0,15²

Тоді: F = qE = 2·10^-9·1,2·10⁴ = 2,4·10^-5 (H).

Відповідь: F=2,4·10^{- 5} Н.

q₁

                      2(1  cos) 

4ob²

                         4                                   

 1,2  10 (B / м).

Приклад 41. Точкові заряди q₁ = 9·10^-9 Кл і q₂ = - 10^-9 Кл перебувають у вакуумі на відстані 1 м один від одного. Знайти точку на прямій, що сполучає ці заряди, в якій напруженість електричного поля рівна нулю.

Розв’язання. Нехай Е₁ – напруженість поля, створеного зарядом q₁, а Е₂ – зарядом q₂. На ділянці АВ прямої, яка проходить через заряди, вектори Е₁ і Е₂ направлені в один і той же бік (мал. 20), тому їх сума не може бути рівна нулю. Зліва від точки А на прямій АВ напруженість Е₁ в будь-якій точці

буде більшою, ніж напруженість Е₂, оскільки заряд q₁ за абсолютною величиною більший, ніж q₂, а відстані r₁ < r₂. На ділянці прямої АВ справа від точки В напруженості Е₁ і Е₂ можуть бути чисельно рівні, тому що q₁ >q₂ і  r₁ > r₂, а так як вони направлені в різні боки, то в точці С сумарна напруженість буде рівна нулю. Позначимо відстань ВС через L. Так, як в точці С вектори Е₁ і

Е₂ по абсолютній величині однакові, то можна записати  

Отримуємо квадратне рівняння відносно L. Його рішення дає корені       L₁ = 0,5 (м) і L₂ = - 0,25 (м). Другий корінь не задовільняє умові задачі. Тому відповідь: справа від q₂ на L = 0,5 м.

Приклад 42.  – частка влітає в плоский горизонтальний конденсатор паралельно до його пластин на однаковій відстані від них. Відстань між пластинами d = 4 см (мал. 21). До пластин прикладено напругу U = 300 В. На якій відстані від початку конденсатора  – частка

потрапить на пластину конденсатора, якщо вона була розігнана різницею потенціалів U₁ = 150 В? 

Розв’язання.  - частка в полі плоского конденсатора буде рухатись подібно до руху в полі тяжіння Землі тіла, кинутого горизонтально (дією сили тяжіння на рух частки нехтуємо, оскільки у цьому випадку вона надзвичайно мала, див. прикл. 37). На частку діє стала електрична сила F . 

Під дією сили  - частка отримує прискорення a  і, пройшовши по           горизонталі          шлях s        за       час    t           ,         відхилиться          на           відстань                

h .

Звідси: .

Кінетична енергія  - частки, розігнаної до швидкості v різницею потенціалів U.

Звідси . Підставивши у формулу шляху значення швидкості,

маємо = 0,04 (м).

Відповідь:  - частка потрапить на пластину конденсатора на відстані 4 см від точки входження в простір конденсатора.

Приклад 43. Кулька масою 1 г з зарядом 5·10^-8 Кл переміщається з точки А, потенціал якої 600 В, в точку В, потенціал якої рівний нулю. Якою була швидкість кульки в точці А, якщо в точці В вона стала рівною 0,4 м/с?

Розв’язання. Робота сил електричного поля рівна зміні кінетичної енергії кульки: A = W_к. Або: q.

Звідси v1 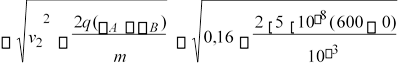  0,32(м / c)

Відповідь: v₁ = 0,32 м/с.

Приклад 44. Два конденсатори ємністю С₁ = 2 мкФ і С₂ = 4 мкФ сполучили послідовно і під’єднали до джерела з напругою U = 75 В. Знайти заряди на обкладках конденсаторів і напругу на кожному з них. 

Розв’язання. Якщо при підключенні батареї до джерела з напругою U на обкладці 1 (мал. 22) виникне заряд q₁, то внаслідок електростатичної індукції на обкладці 2 виникне заряд q₂ = - q₁. Так як обкладки 2 і 3 ізольовані від джерела напруги і електрично нейтральні, то поява заряду на обкладці 2

викличе появу на обкладці 3 заряду q₃ = - q₂ = - (- q₁) = q₁. Це, в свою чергу, викличе появу на обкладці 4 заряду q₄ = - q₁. Таким чином, при послідовному сполученні конденсаторів заряди на його обкладках рівні за величиною. Така рівність не залежить від числа конденсаторів. З малюнка видно, що: U₁ = ₁ - ₂, U₂ = ₃ - ₄, U = ₁ - ₄.

Враховуючи, що поверхня провідника при стаціонарному розподілі зарядів є еквіпотенціальною (₂ = ₃), то: U₁ + U₂ = ₁ - ₂ + ₂ - ₄ = ₁ - ₄ = U, тобто, напруга, підведена до батареї послідовно сполучених конденсаторів, рівна сумі напруг на окремих конденсаторах.

За формулою ємності конденсатора: C, C, C , де С - загальна ємність батареї конденсаторів.

Використовуючи попередні рівності, маємо:  або .

Звідки ємність батареї C .

Величина зарядів на обкладках конденсаторів: q Кл.

Напруги на конденсаторах:

U B; U B.

Відповідь: q₁ = q₂ = q₃ = q₄ = 1·10^-4 Кл, U₁ = 50 B, U₂ = 25 B. 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Вищий рівень

3.1. Однакові металеві кульки заряджені однойменно зарядами q і 4q, розташовані на відстані r одна від одної. Кульки доторкнули на мить одну до одної. На яку відстань їх треба розвести, щоб сила взаємодії не змінилась? 

3.2. Заряди 40 і –10 нКл розташували на відстані 10 см один від одного. Який треба взяти третій заряд і де його розташувати, щоб система перебувала в рівновазі? 

3.3. Заряди по 0,1 мкКл розташували на відстані 6 см один від одного.

Визначити напруженість поля в точці, віддаленій на 5 см від кожного з зарядів. Рішити задачу для випадків: а) обидва заряди однойменні; б) заряди різнойменні. 

3.4. Два заряди, один з яких за модулем у 4 рази більший від другого, розташували на відстані а один від одного. У якій точці поля напруженість дорівнює нулеві, якщо заряди однойменні? Різнойменні? 

3.5. В основі рівностороннього трикутника із стороною а розташовані заряди по +q кожний, а у вершині -q. Визначити напруженість поля в центрі трикутника 

3.6. На відстані 3 см від заряду 4 нКл, розташованого в рідкому діелектрику, напруженість поля становить 20 кВ/м. Визначити діелектричну проникність діелектрика. 

3.7. Між двома пластинами горизонтального конденсатора, віддалених на 4,8 мм одна від одної, у вакуумі перебуває в рівновазі негативно заряджена крапля масла, маса якої 10 нг. Скільки надлишкових електронів має крапля, якщо на пластини подано напругу 1 кВ? 

3.8. У деяких двох точках поля точкового заряду напруженість відрізняється в 4 рази. У скільки разів відрізняються потенціали цих точок поля? 

3.9. На скільки зміниться потенціальна енергія взаємодії зарядів 25 і         –4 нКл, якщо відстань між ними збільшити з 10 до 20 см? 

3.10. Конденсатор ємністю С₁ зарядили до напруги U₁ = 500 В. Коли цей конденсатор паралельно приєднали до незарядженого конденсатора ємністю   С₂ = 4 мкФ, вольтметр показав напругу U₂ = 100 В. Визначити ємність С₁. 

3.11. В імпульсному фотоспалаху лампа живиться від конденсатора ємністю 800 мкФ, зарядженого до напруги 300 В. Визначити енергію спалаху і середню потужність, якщо тривалість розряду 2,4 мс.

Оптимальний рівень

3.12. Дві кульки з однаковим зарядом розташовані на відстані 10 см одна від одної і взаємодіють з силою 0,23 мН. Визначити кількість надлишкових електронів на кожній кульці. 

3.13. У деякій точці поля на заряд 2 нКл діє сила 0,4 мкН. Визначити напруженість поля в цій точці. 

3.14. Електрон перемістився в прискорюючому полі з точки, потенціал якої 200 В, у точку з потенціалом 300 В. Визначити кінетичну енергію електрона, зміну потенціальної енергії взаємодії з полем і набуту швидкість. Електрон починає рух з стану спокою. 

3.15. Електрон, рухаючись під дією електричного поля, збільшив свою швидкість з 10 до 30 Мм/с. Яка різниця потенціалів між початковою і кінцевою точками переміщення? 

3.16. Напруга між двома точками поля, що лежать на одній лінії напруженості однорідного поля, дорівнює 2 кВ. Відстань між цими точками 10 см. Яка напруженість поля? 

3.17. У скільки разів зміниться ємність конденсатора, якщо площу його пластин зменшити у 2 рази, а відстань між ними у 3 рази? 

3.18. При введенні у простір між пластинами повітряного конденсатора твердого діелектрика напруга на конденсаторі зменшилась з 400 В до 50 В. Яку діелектричну проникність має діелектрик? 

3.19. У скільки разів зміниться енергія конденсатора, якщо напругу на ньому збільшити у 4 рази? 

3.20. Є три конденсатори ємностями 2 мкФ, 4 мкФ і 6 мкФ. Які ємності можна отримати при їх сполученні між собою?

Якісні завдання

3.21. Як вводиться поняття напруженості електричного поля?

А) E ; Б) E ; B) E ; Г) E .

3.22. Чому дорівнює напруженість електричного поля всередині провідника у випадку рівноваги?

А) значенню напруженості на поверхні провідника; Б) нулю.

3.33. Що відбувається всередині діелектрика при поміщенні його в електричне поле?

А) виникає додаткове поле, яке підсилює зовнішнє; Б) всередині діелектрика виникає додаткове поле, яке послаблює зовнішнє.

3.34. Як залежить робота А по переміщенню електричного заряду між двома точками електричного поля?

А) пропорційна довжині траєкторії, по якій переміщується заряд; Б) не залежить від траєкторії.

3.35. З якою метою між обкладками конденсатора розміщують діелектрик?

А) для збільшення пробивної міцності; Б) для збільшення ємності; В) для зменшення ємності.

3.36. Чому не можна необмежено зменшувати відстань між обкладками конденсатора?

А) відбудеться пробій; Б) різко зросте ємність.

3.37. Заряджений конденсатор приєднали паралельно до такого самого незарядженого конденсатора. Як змінилась енергія поля?

А) не змінилась; Б) зменшилась у 4 рази; В) зменшилась у 2 рази; Г) збільшилась у 2 рази.

3.38. Тіло, ковзаючи по похилій площині, наелектризувалось. Чи вплине це на тривалість ковзання і швидкість руху в кінці площини?

3.39. В однорідному електричному полі помістили металеву кулю. Чи залишиться поле однорідним поблизу поверхні кулі?

3.40. Чи варто старанно терти сухою тканиною поверхню лакованих меблів, щоб надовго очистити їх від пилу?

3.41. В однорідному електричному полі на однаковій відстані від двох пластин розміщені електрон і протон. Чи з однаковою швидкістю вони досягнуть пластин?

3.42. Чи зміниться притягання двох точкових різнойменних зарядів, якщо посередині лінії, яка їх сполучає, поставити перпендикулярно велику металеву пластину?

3.43. Чи зміниться ємність плоского конденсатора, якщо одна з його пластин паралельно зміститься?

3.44. Чи виконуємо ми роботу, виводячи рухомі пластини конденсатора з нерухомих під час настроювання приймача на бажану радіостанцію?

3.45. Яке сполучення конденсаторів – паралельне чи послідовне більше

«боїться» пробою?

 

3.2. ЕЛЕКТРИЧНИЙ СТРУМ

Електричним струмом називається направлений впорядкований рух електричних зарядів. Для його існування необхідно: створити і підтримувати напругу (різницю потенціалів) між двома точками кола; наявність провідного замкненого кола, по якому відбувається перенесення зарядів завдяки енергії джерела струму. За напрям електричного струму прийнято напрям руху позитивних зарядів в полі, створеному джерелом струму.

Величина заряду q, що протікає через поперечний переріз провідника за одиницю часу t, називається силою струму I:

                                                                  I                                                 (3.15)

Закон Ома для ділянки кола: струм І у провіднику прямо-пропорційний напрузі U на кінцях провідника і обернено пропорційний опору R провідника:

                                                          I                                                   (3.16)

Опір провідника обумовлений втратами енергії електронів при їх зіткненні або розсіянні при взаємодії з додатньо зарядженими іонами речовини.

Тому опір провідника залежить від його довжини l, площі поперечного перерізу

l

S і матеріалу (питомого опору ): R                                                     (3.17)

S

Опір провідника змінюється із зміною температури:

                                                                         RR₀(1T)                                       (3.18)

де: R₀ i R_t - опір провідника при температурі 0 i t С відповідно;  - температурний коефіцієнт опору.

Для послідовного сполучення резисторів загальний опір дорівнює сумі опорів усіх резисторів:  R  R_i  (3.19)

1

Для паралельного сполучення резисторів загальна провідність (      ) рівна R

сумі провідностей усіх резисторів:

                                                                                                    1          1

                                                                            R^_Ri                                        (3.20)

Закон Ома для повного кола: струм I у колі прямо пропорційний електрорушійній силі E джерела струму і обернено пропорційний сумі

зовнішнього R і внутрішнього r опорів: I _ ^ (3.21) R  r

Звідси слідує:  = I(R + r) = IR + Ir = U₁ + U₂  (3.22) де: U₁ - робота джерела струму по перенесенню заряду по зовнішній ділянці кола, U₂ - робота по перенесенню заряду всередині джерела.

При послідовному сполученні n однакових джерел:

                                                               I                                                (3.23)

                   При паралельному сполученні: I                                            (3.24)

де: І - струм в колі;  - е.р.с. одного елемента; r - внутрішній опір одного елемента; R - опір зовнішньої ділянки кола.

При проходженні заряду q по ділянці кола електричне поле виконує

роботу:       A = qU = UIt,        (3.25) де U = ₁ - ₂ – різниця потенціалів електричного поля на кінцях провідника.

Якщо енергія електричного поля в провіднику переходить в тепло, то згідно закону Джоуля-Ленца: кількість виділеної теплоти Q прямо пропорційна квадрату струму, опору провідника і часу проходження струму по провіднику: 

                                                               Q = I²Rt                                              (3.26)

Користуючись законом Ома для ділянки кола можемо також записати:

                                                             Q                                        (3.27)

Потужність в електричному колі:

                                                                                     dA              2                 U2

    P      IU  I R           (3.28) dt      R

Якщо джерело струму з е.р.с. ε і внутрішнім опором r замкнене на зовнішній опір R, то потужність у зовнішній ділянці кола:

                                                        P₁  IU  I²R,                                            (3.29)

Загальна потужність, яку розвиває джерело струму:

          P ,        (3.30) і ККД джерела: 

                                                   .                             (3.31)

Згідно із законом Фарадея, маса речовини, що виділяється при електролізі, пропорційна заряду, який пройшов через електроліт:

                                                           m = kq = kIt,                                           (3.32)

де: І - сила струму в колі; t - час його проходження; k - електрохімічний еквівалент, чисельно рівний кількості речовини, яка виділяється на електроді при проходженні одиниці заряду.

Другий закон Фарадея стверджує, що електрохімічні еквіваленти речовин пропорційні атомним масам А цих речовин і обернено пропорційні їх валентностям n:

                                                           k  C_x,                                          (3.33)

де: С = 1,036·10^-5 г-екв/Кл – стала величина для всіх речовин;  х – хімічний еквівалент речовини. 

Величина F 96500 Кл/г-екв = 9,65·10⁷ Кл/кг-екв називається числом Фарадея.

                 Об’єднаний закон Фарадея m = Cxq It.                                    (3.34)

 

Приклади розв’язання задач

Приклад 45. Батарея з е.р.с. Е = 6 В і внутрішнім опором r = 1,4 Ом живить зовнішнє коло, яке складається з двох паралельних резисторів R₁ = 2 Ом і R₂ = 8 Ом. Визначити різницю потенціалів на затискачах батареї і сили струмів у резисторах.

Розв’язання. Опір паралельно сполучених резисторів на зовнішній ділянці кола R        =1,6 (Ом).

Сила струму в колі згідно закону Ома:

I  

Спад напруги на зовнішньому колі U = IR = 2·1,6 = 3,2 (B). Струми, що йдуть через резистори R₁ і R₂:

                I  =1,6 (A); I 0,4 (A).

Відповідь: U = 3,2 B; I₁ = 1,6 A; I₂ = 0,4 A.

Приклад 46. Знайти опір між точками 1 і 2 кола

(мал. 23, а), якщо кожний з трьох резисторів має опір 1 Ом. Опором з’єднувальних провідників знехтувати.

Розв’язання. Точки кола з однаковими цифрами з’єднані           провідниками,     а        це      значить,      що     їх потенціали однакові. Тому схему можна зобразити так, як показано на мал. 23, б. Отримали паралельне сполучення резисторів. Опір кола: .

Звідси  Ом.

Приклад 47. Визначити е.р.с. і внутрішній опір елемента, якщо при замиканні його на резистор опором R₁ = 1,8 Ом в колі йде струм І₁ = 0,7 А, а при замиканні на резистор R₂ = 2,3 Ом струм в колі І₂ = 0,56 А. Яким буде струм короткого замикання?

Розв’язання. Запишемо закон Ома для обох випадків: I.

Оскільки е.р.с. елемента є величина стала, то I₁(R₁ + r) = I₂(R₂ + r).

                   Звідси: r 0,2 (Ом).

Тоді е.р.с. E = I₁(R₁ + r) = 0,7(1,8 + 0,2) = 1,4 (B).

Струм короткого замикання І_кз  

Відповідь: Е = 1,4 В; І_кз=7 А.

Приклад 48. З ніхромової стрічки перерізом S = 0,5 мм² треба виготовити нагрівач електрокип’ятильника. Яку довжину стрічки потрібно взяти, щоб        V = 2 л води за T = 15 хв нагріти від t₁ = 10 C до t₂ = 100 С? Напруга на затискачах кип’ятильника U = 120 В, його ККД  = 70%.

Розв’язання. Для нагрівання води потрібно затратити кількість теплоти  Q₁ = cm(t₂ - t₁), де: с- питома теплоємність води. 

Для цього від нагрівача потрібно взяти кількість теплоти Q, де:    R - опір нагрівника, рівний R - питомий опір ніхрому). На основі закону

збереження енергії Q₁ = Q₂, або cm. Звідси: L . Обчислення дають: L  6 (м).



Відповідь: L  6 м. 

Приклад 49. Металевий диск з радіусом R = 20 см обертається з частотою n = 30 об/с. Визначити різницю потенціалів між центром та краєм диску.

Розв’язання. В системі відліку, пов’язаною з електроном, на нього діють дві сили: відцентрова сила інерції F_і, яка зміщує його на периферію диска, та електростатична F_e, що виникає за рахунок зміщення зарядів від центру. Зміщення електронів відбуватиметься доти, поки ці сили стануть рівними за модулем. Якщо маса електрона m, а його заряд q, то: .

Звідси  . Оскільки v = R = 2nR, то  .

Обчислимо:   

Відповідь:  = 8,075·10^-9 В.

Приклад     50.     Міліамперметр    зі       шкалою      на               І₁ = 20 мА необхідно використати як амперметр для вимірювання струмів силою до І₂ = 5 А. Розрахувати опір шунта R, якщо внутрішній опір міліамперметра r = 8 Ом. 

Розв’язання. Шунт приєднується до міліамперметра паралельно (мал. 24). Це значить, що через нього повинен проходити струм     (І₂ - І₁), а через міліамперметр – струм І₁. Для паралельного сполучення            (I₂  - I₁)R = I₁r. Звідки: R 0,032 (Ом).

Відповідь: опір шунта повинен бути рівний 0,032 Ом.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Вищий рівень

3.46. Визначити швидкість   упорядкованого   руху електронів в алюмінієвому проводі перерізом 5 мм² при силі струму 10 А, якщо концентрація електронів провідності в алюмінію становить 5·10²⁸ м^-3.

3.47. Від джерела напругою 45 В необхідно живити нагрівальну спіраль, яка має опір 20 Ом і розрахована на напругу 30 В. Є три реостати, на яких написано: 1) 6 Ом, 2 А; 2) 30 Ом, 4 А; 3) 800 Ом, 0,6 А. Який з цих реостатів потрібно взяти?

3.48. Міліамперметр з опором 3 Ом і межею вимірювання до 25 мА зашунтували нікеліновим провідником довжиною 20 см і діаметром 2 мм. При ввімкненні приладу в коло виявилось, що стрілка приладу зупинилась на поділці 20 мА. Яка сила струму в колі? 

3.49. Два елементи з е.р.с. Е₁ = 1,5 В і Е₂ = 2 В з’єднані однаковими полюсами. Вольтметр, приєднаний до клем батареї, показав напругу 1,7 В. Визначити відношення внутрішніх опорів елементів. 

3.50. Фоторезистор, який у темряві має опір 25 кОм, ввімкнули послідовно з резистором, що має опір 5 кОм. Коли резистор освітили, то сила струму у колі збільшилась у 4 рази. У скільки разів зменшився опір фоторезистора? 

3.51. Який додатковий опір необхідно приєднати до вольтметра, що має внутрішній опір 5 кОм, щоб граничне значення вимірюваної напруги збільшилось в 5 разів? 

3.52. Який опір повинен мати шунт, щоб при його приєднанні до амперметра з внутрішнім опором 0,018 Ом граничне значення вимірюваного струму збільшилось у 10 разів?

3.53. Тролейбус масою 11 т рухається рівномірно з швидкістю 36 км/год. Визначити силу струму в обмотці двигуна, якщо напруга дорівнює 500 В, а ККД 80%. Коефіцієнт опору рухові становить 0,02.

3.54. Електрокип’ятильник із спіраллю, опір якої 160 Ом, опустили в посудину, що містить 0,5 л води при температурі 20 С, і ввімкнули в мережу з напругою 220 В. Через 20 хв. кип’ятильник вимкнули. Яка кількість води википіла, якщо спіраль має ККД 80%?

3.55. Електродвигун підйомного крана працює під напругою 380 В і споживає струм 20 А. Який ККД має кран, якщо вантаж масою 1 т він піднімає на висоту 19 м за 50 с?

3.56. Знайти внутрішній опір та е.р.с. джерела струму, якщо при силі струму 30 А потужність у зовнішньому колі дорівнює 180 Вт, а при силі струму 10 А ця потужність дорівнює 100 Вт.

3.57. Лампочки, опори яких дорівнюють 3 і 12 Ом, по черзі приєднують до джерела струму, і вони при цьому споживають однакову потужність. Визначити внутрішній опір джерела струму і ККД кола у кожному випадку.

3.58. Джерело струму з внутрішнім опором r і е.р.с. E замкнуто на три лампочки опором 3r кожна, сполучених послідовно. У скільки разів зміниться сила струму в колі, напруга на затискачах джерела і корисна потужність, якщо лампочки з’єднати паралельно?

3.59. Скільки часу тривало нікелювання, якщо на виробі осів шар нікелю масою 1,8 г? Сила струму становить 2 А.

3.60. Скільки витрачається електроенергії на рафінування 1 т міді, якщо напруга на електролітичній ванні дорівнює 0,4 В?

Оптимальний рівень

3.61. Чи можна вмикати в мережу з напругою 220 В реостат, на якому написано: а) 30 Ом; 5 А; б) 2000 Ом; 0,2 А?

3.62. Опір обмотки електромагніта, виготовленого з мідного дроту, при температурі 20 С був 2 Ом, а після тривалої роботи став 2,4 Ом. До якої температури нагрілась обмотка?

3.63. В електричній плитці, розрахованій на напругу 220 В, є дві спіралі, кожна з яких має опір 120 Ом. За допомогою перемикача можна ввімкнути в мережу одну спіраль, дві спіралі послідовно або дві спіралі паралельно. Обчислити потужність у кожному випадку.

3.64. Визначити напругу на затискачах джерела струму з е.р.с. 2 В і внутрішнім опором 0,5 Ом до і після під’єднання до нього резистора опором  4,5 Ом. 

3.65. Три провідники з однаковим опором під’єднують до джерела струму спочатку паралельно, а потім послідовно. У якому випадку споживається більша потужність і в скільки разів? 

3.66. Лампа потужністю 300 Вт розрахована на напругу 110 В. Який додатковий опір треба взяти, щоб ввімкнути лампу в мережу з напругою 127 В?  Якісні завдання

3.67. У скільки разів зміниться опір провідника без ізоляції, якщо його зігнути вдвоє і скрутити?

3.68. Чому спіралі електронагрівальних приладів роблять з матеріалу, що має великий питомий опір?

3.69. Як залежить питомий опір провідників від температури? А) квадратично; Б) експоненційно; В) лінійно.

3.70. Чому опір напівпровідників зменшується з підвищенням температури?

А) збільшується середня швидкість направленого руху носіїв заряду; Б) збільшується концентрація носіїв заряду.

3.71. Які домішки у напівпровідниках називають донорними?

А) які збільшують концентрацію дірок; Б) які збільшують концентрацію вільних електронів; В) ті, що не впливають на електропровідність.

3.72. Чи змінюється з часом сила струму в електролітичній ванні? Нагрівання розчину не враховувати.

3.73. Щоб отримати провідність потрібного типу, у напівпровідники вводять домішки фосфору, галію, сірки (сульфуру), бору, арсену (миш’яку), індію або сурми. Які з цих елементів можна вводити у кремній, щоб отримати електронну провідність?

3.74. Терморезистори використовують для вимірювання швидкості течії рідин. На якому принципі базується їх робота?

3.75. В просторі між пластинами створюють несамостійну провідність газу. Як зміниться сила струму насичення. Якщо при незмінній дії іонізатора пластини зблизити?

 

3.3. МАГНІТНЕ ПОЛЕ

При проходженні постійного струму по провідниках спостерігається їх механічна взаємодія – в залежності від напрямів струмів вони відштовхуються або притягуються між собою. Причиною такої взаємодії є поява магнітного поля навколо провідників із струмом.

Силовою характеристикою магнітного поля є індукція В, яка визначає силу F (силу Ампера), що діє на прямолінійний провідник довжиною L зі струмом силою І:

          F_А = IBLsin       (3.35) де  – кут між напрямом вектора В і струмом І.

Напрям сили Ампера визначається за правилом лівої руки: якщо ліву руку розмістити так, щоб силові лінії магнітного поля входили в долоню, витягнуті чотири пальці співпадали з напрямком струму у провіднику, то відведений на 90 великий палець покаже напрям сили Ампера.

Напрям вектора В навколо прямого провідника з струмом визначається за правилом правого гвинта: якщо гвинт обертати так, щоб його поступальний рух співпав з напрямом струму у провіднику, то напрям обертання головки гвинта покаже напрям вектора В (вектор В буде дотичним до траєкторії обертання гвинта).

Напруженість магнітного поля в точці, віддаленій на відстань r від прямого безмежно довгого провідника, по якому проходить струм І, визначається за формулою:  H   (3.36)

На заряд q, що рухається у магнітному полі В з швидкістю v, діє сила

Лоренца F_Л:         F_Л = qvBsin        (3.37) де  – кут між напрямками векторів В і v.

Величина, яка показує у скільки разів індукція магнітного поля у речовині більша, ніж у вакуумі, називається магнітною проникністю речовини  .

Індукція і напруженість магнітного поля пов’язані між собою:

          B = _oH  (3.38) де _о – магнітна проникність вакууму (_о = 12,57·10^-7 Г/м).

Речовини поділяються на: парамагнетики ( > 1), діамагнетики ( < 1) і феромагнетики ( >> 1). Причиною феромагнетизму є утворення в речовині областей спонтанного намагнічення (доменів), які завдяки зміні орієнтації у магнітному полі значно посилюють магнітне поле в речовині.

Магнітним потоком називається фізична величина, чисельно рівна добутку індукції магнітного поля на площу, яку воно пронизує:

          Ф = BScos,         (3.39) де  – кут між вектором В і нормаллю до площадки S. Закон електромагнітної індукції Фарадея:

dФ

                                                                             _i   ,                                         (3.40)

dt

де _i – електрорушійна сила індукції, що виникає при зміні магнітного потоку

Ф за час t. Знак « - » пояснюється правилом Ленца: індукційний струм має такий напрям, що створене ним магнітне поле протидіє зміні магнітного поля, яке цей струм викликає.

dI

                 Електрорушійна сила самоіндукції _is L                                  (3.41)

dt

де L – індуктивність котушки, в якій зміна струму I відбувається за час t.

Енергія магнітного поля котушки з індуктивністю L, по якій проходить

LI²

струм І:                                                 W                                           (3.42)

2

 

Приклади розв’язання задач

Приклад 51. По двох прямих довгих провідниках, які знаходяться на відстані L = 10 см один від одного (мал. 25), у протилежних напрямах проходять струми І₁ = 6,28 А і І₂ = 12,56 А. Визначити напруженість магнітного поля у точці, яка лежить між провідниками на прямій, що їх сполучає, на відстані r=4 см від першого провідника.

Розв’язання. Вектори напруженостей магнітних полів, створених струмами І₁ та І₂ на прямій, що проходить через центри провідників, будуть перпендикулярними до цієї прямої. Для вибраних на мал. 25 напрямів струмів ці вектори будуть направлені вгору. Тому в точці С результуюча напруженість магнітного поля буде: Н = Н₁ + Н₂. Для прямих довгих провідників маємо:

H.

                   Тоді Н = 58 (A/м).

Відповідь: Н = 58 A/м.

Приклад 52. В котушці без сердечника за t = 0,001 с струм зріс від I₁ = 1 А до I₂ = 2 А, при цьому в котушці виникла е.р.с. самоіндукції E=20 В. Визначити коефіцієнт самоіндукції і зміну енергії магнітного поля котушки.

Розв’язання. Е.р.с. самоіндукції E_сі , звідки:

                   L 0,2 (Гн). 

                   Зміна енергії магнітного поля котушки: W 0,3 (Дж). 

Відповідь: L = 0,2 Гн; W = 0,3 Дж. 

Приклад 53. Літак летить горизонтально з швидкістю v = 950 км/год. Вертикальна складова магнітного поля Землі H = 40 А/м. Визначити електрорушійну силу індукції, що виникає на кінцях крил літака, якщо розмах крил d = 12,5 м. 

Розв’язання. Електрорушійна сила залежить від швидкості зміни

магнітного потоку: Е.



Зміна магнітного потоку Ф = ВS.

Зміна площі буде рівна тій площі, яку опишуть крила літака за певний час: S = vdt.

Індукція магнітного поля пов’язана з напруженістю магнітного поля співвідношенням: В = _оН.

Тоді: Е = -_оHvd = -12,57·10^-7·40·263,9·12,5 = 1,67 (B). 

Відповідь: Е = 1,67 В.

Приклад 54. Провідник, по якому проходить струм, перемотують з однієї котушки на іншу. Швидкість перемотування дорівнює швидкості дрейфу електронів у провіднику, але напрямлена у протилежний бік. Чи є магнітне поле навколо провідника у цьому випадку?

Розв’язання. Магнітне поле існує, оскільки рух позитивних іонів решітки створює таке ж магнітне поле, як і рух електронів у провіднику, що перебуває у спокої.

Приклад 55. Протон, що пройшов прискорюючу різницю потенціалів      U = 600 В, влітає в однорідне магнітне поле з індукцією B = 0,3 Тл і рухається по колу. Визначити радіус R кола. 

Розв’язання. При русі протона у магнітному полі сила, що діє з боку поля на протон, створює доцентрове прискорення. Рух буде по коловій траєкторії, якщо врівноважаться дві сили – сила Лоренца F_л і сила інерції F_і: qBv .

Звідси: R .

Швидкість руху протона знайдемо з закону збереження енергії: протон розганяється в електричному полі за рахунок зміни потенціальної енергії. Тому

 qU, звідки                            . Враховуючи це, маємо вираз для обчислення

радіуса траєкторії протона:

2

                                                                              R  1,2 10                                (м)  1,2(см)

Відповідь: радіус траєкторії протона рівний 1,2 см.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Вищий рівень

3.76. Рамка площею 1000 см², що має опір 0,5 Ом, спочатку була розташована паралельно вектору індукції В магнітного поля Землі, а потім повернулась так, що її площина стала перпендикулярною В. Яка кількість електрики протікає через рамку, якщо В = 5·10^-5 Тл? 

3.77. Протон і  – частка влітають в однорідне магнітне поле перпендикулярно до силових ліній. Порівняти радіуси кіл, що їх описують частки, коли в них однакові: а) швидкості; б) енергії. 

3.78. По горизонтально розташованому провіднику завдовжки 20 см і масою 4 г проходить струм силою 10 А. Визначити індукцію (модуль і напрям) магнітного поля, в якому треба розмістити провідник, щоб сила тяжіння врівноважувалась силою Ампера.

3.79. Провідник, що має довжину L і масу m, підвішений на тонких дротинах. Під час проходження по ньому струму І він відхилився в однорідному магнітному полі так, що дротини утворили кут  з вертикаллю. Яка індукція магнітного поля?

3.80. Однорідні електричне і магнітне поле розташовані взаємно перпендикулярно. Напруженість електричного поля становить 1 кВ/м, а індукція магнітного поля 1 мТл. Якими мають бути напрям і значення швидкості електрона, щоб траєкторія його руху була прямолінійною?

3.81. Скільки витків проводу повинна містити обмотка на стальному осерді з поперечним перерізом 50 см², щоб у ній під час зміни магнітної індукції від 0,1 до 1,1 Тл протягом 5 мс збуджувалась е.р.с. індукції 100 В?

3.82. Визначити енергію магнітного соленоїда, в якому при силі струму 10 А виникає магнітний потік 0,5 Вб.

3.83. Рамку площею 40 см² розмістили в однорідному магнітному полі з індукцією 0,1 Тл так, що рамка перпендикулярна до ліній індукції. При якій силі струму на рамку діятиме обертаючий момент 20 мН·м? Оптимальний рівень

3.84. Магнітний потік всередині контуру площею 60 см² становить         0,3 мВб. Визначити індукцію поля всередині контуру, вважаючи поле однорідним. 

3.85. Яка сила діє на протон, що рухається з швидкістю 10 Мм/с в однорідному магнітному полі з індукцією 0,2 Тл перпендикулярно до ліній поля?

3.86. Електрон рухається в однорідному магнітному полі, індукція якого  4 мТл. Визначити період обертання електрона.

3.87. Який магнітний потік виникає в котушці з індуктивністю 20 мГн при силі струму 10 А?

3.88. Яка е.р.с. самоіндукції збуджується в обмотці електромагніта з індуктивністю 0,4 Гн під час рівномірної зміни сили струму в ній на 5 А за   0,02 с?

3.89. По котушці індуктивністю 0,6 Гн проходить струм 20 А. Яку енергію має магнітне поле цієї котушки?

3.90. З якою швидкістю треба переміщати провідник, довжина активної частини якого 1 м, під кутом 60 до ліній магнітного поля, щоб у провіднику збуджувалась е.р.с. індукції 1В? Індукція магнітного поля 0,2 Тл.  Якісні завдання

3.91. На мал. 26 зображені випадки взаємодії магнітного поля і провідника із струмом. Доповніть малюнки до завершення.

3.92. Чи виникатиме індукційний струм у коловому витку, розташованому в однорідному магнітному полі, якщо:

а) переміщати виток поступально;

б) обертати виток навколо осі, яка проходить через його центр

перпендикулярно до площини витка; 

в) обертати виток навколо осі, що лежить у його площині?

3.93. Чому коливання стрілки компаса швидше згасають, якщо корпус приладу латунний, і повільніше – якщо корпус пластмасовий?

3.94. Чи зміниться магнітний потік магніту, якщо збільшити: а) його довжину; б) переріз?

3.95. У якій воді - холодній чи гарячій – звичайний штабовий магніт може підняти більший вантаж?

3.96. Чи порушиться рівновага сили Ампера і ваги тіла, якщо в k разів збільшити діаметр провідника при сталій густині струму?

3.97. Чи може сила Ампера зрівноважити силу тяжіння в провіднику, розміщеному: а) вертикально; б) горизонтально?

3.98. Що таке температура Кюрі?

А) Температура, перевищення якої приводить до зникнення феромагнітних властивостей речовини; Б) температура, при якій змінюється структура речовини.

3.99. Чи можна для виготовлення магнітофонної стрічки взяти мікрокристали того самого сплаву, який використовують у трансформаторах?

3.100. Як вплине на магнітні властивості дія інтенсивних ударів молотком по поверхні: а) постійного магніту; б) стержня з ненамагніченого м’ягкого заліза?

 

 

 

3.4. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ

В генераторах електростанцій створюється е.р.с., яка змінюється за

законом: e = E_o sin (t + _o)                                                                       (3.43)

де: e - миттєве значення е.р.с.; Е_о - її максимальне (амплітудне) значення;         t + _o - фаза коливань е.р.с.;  =^; T - кругова частота; _o - початкова фаза, величина якої залежить від вибору початку відліку часу.

Напруга на затискачах генератора змінного струму змінюватиметься за тим же законом: u = U_o sin (t + _o)  (3.44)

Частота зміни промислового струму у нашій країні за стандартом рівна 50 Гц, тобто його період 0,02 с.

Якщо до генератора змінної е.р.с., на затискачах якого напруга змінюється за законом u = U_o sint, приєднати зовнішнє коло, то в ньому буде проходити струм I = I_o sin (t - ) (3.45)

де:  - різниця (зсув) фаз між струмом і напругою, яка залежить від виду навантаження (активного чи реактивного) у зовнішньому колі.

Діючі (ефективні) значення е.р.с. Е, напруги U і струму І зв’язані з їх максимальними (амплітудними) значеннями таким чином: 

                                                                                     E                U                I_o

                                                                                            E ,U , I .                                          (3.46)

 

Якщо до джерела напруги u= U_o sint послідовно приєднати активний опір R, конденсатор ємністю С і котушку індуктивністю L, то закон Ома для такого кола матиме вигляд

               Z                                                                   (3.47)

Величина X_L = L = 2L називається індуктивним, а X_C  – ємнісним опором. Різниця X_L -- являє собою реактивний опір в колі змінного струму.

Зсув фаз між струмом і напругою визначається з виразу

                                                            )/R                                   (3.48)

За умови, коли X_L - X_C = 0, струм в колі досягає максимального значення: 

I  – електричний резонанс. Звідси маємо:

1

                                                                                       LC ,T  2 LC                                   (3.49)

 

Відношення активної потужності Р в колі змінного струму до повної потужності P₁ = IU називається коефіцієнтом потужності (cos): 

                                                     ) або P = IU (cos)                       (3.50)

де:  – зсув фаз між струмом і напругою. 

Для перетворення змінного струму однією напруги в змінний струм іншої напруги використовують трансформатори. Між напругами (U₂, U₁) вторинної і первинної обмоток трансформатора і числом витків в них (n₂, n₁) існує

співвідношення  k,    (3.51) де k – коефіцієнт трансформації трансформатора.

Джерелом електромагнітних коливань і хвиль є змінні струми. Їх можна отримувати в коливальних контурах – пристроях, які складаються з котушки індуктивністю L і конденсатора ємністю С. Період коливань контура за відсутності втрат енергії визначається з формули Томсона:

                                                                T 2 LC                                         (3.52)

В коливальному контурі відбувається перетворення енергії електричного поля конденсатора в енергію магнітного поля котушки і навпаки.

Швидкість поширення електромагнітної хвилі у вакуумі рівна швидкості

поширення світла (с = 3·10⁸ м/с), а довжина хвилі:            (3.53) 

 

Приклади розв’язання задач

Приклад 57. В магнітному полі з індукцією В = 0,5 Тл обертається з швидкістю n = 300 об/хв прямокутна рамка площею S = 400 см². Визначити період T і максимальне значення е.р.с. E_o в рамці, якщо вісь обертання перпендикулярна до поля.

Розв’язання. Нехай довжина рамки а, ширина b, тоді площа рамки S = аb (мал. 27). При обертанні рамки е.р.с. індукції виникає лише в сторонах рамки а, оскільки лише вони перетинають силові лінії магнітного поля. Миттєве значення е.р.с. в рамці e = BLvsin , де: L = 2а; v - лінійна швидкість руху кожної сторони рамки а,  = t = 2nt - кут повороту рамки за час t, якщо початок відліку часу брати від моменту, коли площина рамки перпендикулярна до поля. Лінійна швидкість руху сторони а: . 

Тому e BnS sint, де: 2BnS = Е_о – амплітудне

значення е.р.с. індукції в рамці;  – фаза коливань е.р.с.; T  – період коливань е.р.с.

Підставимо числові значення і обчислимо:

Е_о =2BnS = 2·3,14·0,5·5·4·10^-2 = 0,63 (В); Т  

Відповідь: Е_о = 0,63 В; Т = 0,2 с.

Приклад 58. Визначити індуктивність котушки, якщо амплітуда змінної напруги на її кінцях U_o = 157 В, амплітуда струму в ній І_о = 5 А і частота струму  = 50 Гц. Активним опором котушки знехтувати.

Розв’язання. Оскільки ємнісним опором Х_С і активним опором котушки нехтуємо, то повний опір буде: 

Z  R2  (XL  XC)2  XL L  2L

За законом Ома Z , тому 2L .

Звідки L .

Відповідь: L = 0,1 Гн.

Приклад 59. До мережі змінного струму з ефективною напругою 127 В приєднали коло, яке складається з послідовно ввімкнених активного опору 100 Ом і конденсатора ємністю 40 мкФ. Визначити амплітуду струму в колі.

Розв’язання. Частота промислового струму прийнята рівною 50 Гц.

Ємнісний опір X_C  

Повний опір кола ^{Z }

                    Амплітудне значення струму        0                                . Розв’язавши ці рівняння,

отримаємо: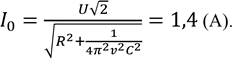

Відповідь: І_о = 1,4 А.

Приклад 60. Визначити ємність конденсатора коливального контура, якщо відомо, що при індуктивності L=100 мкГн контур настроєно в резонанс на електромагнітні коливання з довжиною хвилі  = 300 м.

Розв’язання. Період власних коливань в коливальному контурі визначається за формулою Томсона: 



T  c  2 LC,

де: с = 3·10⁸ м/с – швидкість поширення електромагнітних хвиль. Маємо, що   

C  

Відповідь: С=2,5·10^-10 Ф = 250 пФ. 

Приклад 61. У коло промислової частоти ввімкнули послідовно лампочку, конденсатор ємністю С = 20 мкФ і котушку, яка без осердя має індуктивність L₁ = 0,1 Гн, а при повністю введеному осерді індуктивність         L₂ = 1 Гн. Як змінюватиметься розжарення лампи в міру введення в котушку осердя?

Розв’язання. Розжарення лампи пов’язане з виділенням на активному опорі нитки розжарювання тепла, кількість якого згідно закону Джоуля-Ленца Q=I²Rt, де І – сила струму, який протікає через нитку, R - її опір, t - час проходження струму. При заданому часі проходження струму, враховуючи, що опір нитки розжарення мало змінюється з температурою, можна вважати, що зміна кількості теплоти в основному визначається зміною струму. При введенні в котушку осердя змінюється її індуктивність. Проаналізуємо залежність

U

струму від індуктивності: ^{I }       2  (L 1/C)2 ^. Звідси видно, що струм, а R

значить і кількість теплоти будуть найбільшими, коли підкореневий вираз в дужках рівний нулю, тобто, коли L . Побудуємо графік залежності реактивного опору від зміни індуктивності котушки, тобто залежність R_x  

(мал. 28). З малюнка бачимо, що в проміжку від 0 до 0,5 Гн реактивний опір по модулю спадає, а тому струм, а значить і кількість теплоти зростає. При подальшому зростанні L, що відбувається за рахунок введення осердя в котушку, реактивний опір зростає, а тому і розжарення лампочки буде зменшуватись.

Приклад 62. Контур має у своєму складі індуктивність L, малий опір R та ємність С. Яку потужність потрібно підвести до контуру, щоб у ньому підтримувались незгасаючі коливання при яких максимальна напруга на конденсаторі дорівнює U_o?

Розв’язання. Потужність, яка підводиться до контуру, розсіюється, переважно, на опорі R. Тому P = I_ефR. Але І_еф . Максимальна сила струму І_max може бути отримана за максимальним значенням напруги на конденсаторі,

яка виникає при коливаннях у контурі. Це значення буде І_еф  . В цих розрахунках вважаємо, що величина опору R настільки мала, що не виливає на період власних коливань у контурі. Тому маємо: P .

.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Кількісні задачі

3.      101. Неонова лампа починає світитись, коли напруга на її електродах досягає точно визначеного значення U₁. Яку частину періоду світитиме лампа, якщо її ввімкнути в мережу, діюче значення напруги в якій дорівнює U₁?

3.102.             У коло змінного струму частотою  ввімкнули послідовно активний опір R і котушку індуктивністю L. Конденсатор якої ємності С потрібно ввімкнути послідовно в коло, щоб коефіцієнт потужності дорівнював 1?

3.103.             Скільки витків має рамка площею 500 см², якщо при обертанні її з частотою 20 с^-1 в однорідному магнітному полі з індукцією 0,1 Тл, амплітудне значення е.р.с. дорівнює 63 В?

3.104.             Конденсатор, який має ємність 10 мкФ, зарядили до напруги 400 В і приєднали до котушки. При цьому у контурі виникли згасаючі коливання. Яка кількість теплоти виділиться в контурі за час, протягом якого амплітуда напруги зменшиться у 2 рази.

3.105.             У коливальному контурі індуктивність котушки становить 0,2 Гн, а амплітуда сили струму дорівнює 40 мА. Визначити енергію електричного поля конденсатора і магнітного котушки в той момент, коли миттєве значення сили струму буде в 2 рази меншим, ніж амплітудне значення.

3.106.             Який діапазон частот власних коливань у контурі, якщо його індуктивність можна змінювати в межах від 0,1 до 10 мкГн, а ємність – у межах від 50 до 5000 пФ?

3.107.             Ротор генератора має 50 пар полюсів і обертається з частотою 2400 об/хв. Е.р.с. якої частоти збуджується у цьому генераторі?

3.108.             Трансформатор підвищує напругу від 220 до 660 В і містить у первинній обмотці 840 витків. Який коефіцієнт трансформації? Скільки витків міститься у вторинній обмотці? У якій обмотці провід має більший поперечний переріз?

3.109.             Знижувальний трансформатор з коефіцієнтом трансформації 10 ввімкнули у мережу з напругою 220 В. Яка напруга на виході трансформатора, якщо опір вторинної обмотки 0,2 Ом, а опір корисного навантаження 2 Ом?

3.110.             Скільки коливань відбувається в електромагнітній хвилі завдовжки 30 м протягом одного періоду звукових коливань з частотою 200 Гц? Якісні завдання

3.111.             У коло змінного струму ввімкнули послідовно конденсатор, котушку без осердя і лампу розжарення. Про поступовому введенні осердя лампа спочатку світиться усе яскравіше, а потім розжарення нитки починає зменшуватись. Чому?

3.112.             Як залежить ємнісний опір від частоти струму?

А) прямопропорційно; Б) оберненопропорційно; В) не залежить.

3.113.             Як залежить величина індуктивного опору від частоти струму? А) не залежить; Б) оберненопропорційно; В) прямопропорційно.

3.114.             На якому явищі базується принцип дії трансформатора?

А) на явищі електромагнітної індукції; Б) на явищі залишкового намагнічення заліза.

3.115.             Чи збігаються по фазі коливання струму та напруги на активному опорі в колі змінного струму? А) так; В) ні.

3.116.             Яка орієнтація вектора швидкості світла с по відношенню до векторів напруженості електричного поля Е та індукції магнітного поля В в електромагнітній хвилі?

А) с  Е, с  В, Е  В. Б) с  Е, Е  В. В) с  Е, Е  В.

          

4.      ОПТИКА

Відбивання світла

Будь-яка відбиваюча поверхня перетворює падаючі на неї промені так, що кут падіння променя дорівнює куту відбивання і відбитий та падаючий промені лежать в одній площині з перпендикуляром, опущеним на поверхню в точці падіння.

Якщо промені, що падають на плоску поверхню поділу двох середовищ паралельним пучком і після відбивання залишаються паралельними, то відбивання називають дзеркальним, а саму поверхню — плоским дзеркалом. Пучок променів, що падає із точкового джерела А на плоске дзеркало OO', перетворюється дзеркалом так, що (мал. 29): 

1) продовження всіх відбитих променів буде перетинатись в точці А', яка є уявним зображенням точки А. Для спостерігача, око якого розміщене у відбитому потоці, буде здаватися, що промені виходять не з точки А, а з точки

А';

2)                віддаль від зображення до площини дзеркала дорівнює віддалі від цієї площини до предмета;

3)                зображення протяжного предмета в плоскому дзеркалі дорівнює по розмірах самому предмету і розміщене симетрично відносно площини дзеркала. Заломлення світла

 Відношення швидкості поширення світла с у вакуумі до швидкості v₁ поширення світла в даному середовищі називають абсолютним показником заломлення цього середовища: n  (4.1)

Якщо промінь світла переходить із середовища з абсолютним показником заломлення n₁ в середовище з показником заломлення n₂, то показник заломлення другого середовища відносно першого дорівнює:

                                                         n                                    (4.2)

де  - кут падіння;   - кут заломлення. Якщо промінь світла проходить з оптично менш густого середовища в оптично більш густе, то n₁ < n₂, тоді,  <   тобто заломлений промінь відхиляється від свого початкового напрямку, наближаючись до перпендикуляра, поставленого в точку падіння променя на межі поділу двох середовищ. 

Прозоре для світлових променів тіло, яке обмежене двома (переважно сферичними) заломлюючими поверхнями, називається лінзою. Лінза, в якій центральна частина товща від її країв, називається збірною, а лінза, краї якої товстіші, ніж центральна частина - розсіювальною.

Паралельний пучок променів, що падає на опуклу лінзу, після заломлення в лінзі сходиться в одній точці, яка називається фокусом. Якщо паралельні промені падають на розсіювальну лінзу, то після заломлення вони розходяться так, що їх продовження перетинаються в точці, яка називається фокусом розсіювальної лінзи (мал. 30).  

Лінія, що проходить через центр лінзи і обидва її фокуси називається головною оптичною віссю. Будь-яка інша лінія, що проходить через центр лінзи, називається побічною віссю. Дві паралельні площини, що проходять через фокуси лінзи, перпендикулярно до її головної оптичної осі, називаються фокальними площинами. Площина, що проходить через центр лінзи перпендикулярно до її головної оптичної осі, називається головною площиною.

При побудові зображення світної точки або предмета в лінзі вибирають два з чотирьох характерних променів (мал. 31): 

1.       Промінь,     що проходить через оптичний центр лінзи, не зазнає заломлення. 

                2      Промінь,      що      йде

паралельно до будь-якої оптичної осі, після заломлення повинен пройти через фокус, що лежить на цій оптичній осі. Якщо світна точка лежить на головній оптичній осі, то для побудови зображення треба провести побічну оптичну вісь. 

3.                 Промінь, що проходить через передній фокус після заломлення повинен йти паралельно до головної оптичної осі. 

4.                 Промінь, що проходить через передній подвійний фокус лінзи, повинен пройти через задній подвійний фокус.

Для розсіювальної лінзи справедливі ті ж самі міркування з врахуванням того, що фокуси її уявні.

Якщо F – фокусна віддаль лінзи, n_ - показник заломлення середовища, n_cp показник заломлення матеріалу в якому  перебуває лінза, R₁ i R₂ - радіуси

кривизни однієї і другої поверхні лінзи, то )              (4.3)

Радіус кривизни опуклої поверхні береться зі знаком (+), вгнутої зі знаком ( -). Оптична сила лінзи D визначається формулою D  i вимірюється в діоптріях (дптр). Одна діоптрія - оптична сила лінзи, яка має фокусну віддаль 1 м. 

                Для тонкої лінзи має місце співвідношення ±,                     (4.4)

де знак (+) - для збиральної лінзи, знак (-) - для розсіювальної лінзи, a – віддаль від предмета до лінзи, b - віддаль від зображення предмета до лінзи.

Хвильові властивості світла

Такі явища, як інтерференція, дифракція і дисперсія визначають хвильові властивості світла. Інтерференція, це  явище накладання хвиль з посиленням коливань точок середовища в одних зонах (максимумах) і послабленням в інших (мінімумах); при цьому відбувається перерозподіл енергії в просторі. Когерентними називають світлові хвилі, які мають однакові частоти коливань і різниця фаз яких залишається постійною в часі.

               Умова максимуму інтерференції світла  = 2k ^                              (4.5)

                Умова мінімуму інтенсивності світла                                 ^ (4.6)

При інтерференції світла в тонких плоскопаралельних пластинках у відбитому світлі умови максимуму і мінімуму інтенсивності світла виражаються співвідношеннями:

             (Умова max)  = 2hn соsr ^ k ^                                                (4.7)

              (Умова min)  = 2hn соsr + ^ = (2k+1) ^.                                          (4.8)

де h - товщина тонкої пластинки; n - показник заломлення матеріалу пластинки; r - кут заломлення світла в ній. При інтерференції світла в проходячому світлі умови максимуму і мінімуму міняються місцями. 

Прохід через отвори чи огинання малих перешкод приводить до відхилення поширення енергії світла від прямолінійного. Це явище називають дифракцією світла. 

Дифракційна ґратка - система великої кількості вузьких паралельних щілин шириною d₁, розділених непрозорими проміжками d₂. Величина               d = d₁ + d₂ - називається періодом ґратки.

 У дифракційній ґратці максимуми освітленості спостерігаються в напрямах, що утворюють з нормаллю до ґратки кути , які задовольняють таке співвідношення:

          d sin = k          (4.9) k = 1, 2, 3 ... - ціле число (порядок спектра). 

Дисперсією світла називається явище залежності показника заломлення світла від довжини світлової хвилі.

 

Приклади розв’язування задач

Приклад 63. За який час світло пройде відстань, рівну довжині конуса тіні, яку відкидає Земля у сонячних променях? Радіус Землі R_з = 6,4·10⁶ м; радіус Сонця R_c = 7·10⁸ м, відстань від Землі до Сонця а = 1,5·10¹¹ м. Впливом атмосфери знехтувати.

Розв’язання. Збіжний конус тіні, яку відкидає Земля в сонячних променях, обумовлено тим, що розміри Землі менші, ніж розміри Сонця. З мал. 32 видно, що радіуси Землі і Сонця без врахування впливу атмосфери пов’язані з розмірами земної орбіти залежністю: , де х – довжина конусу тіні Землі.

Звідси: x  

В однорідному середовищі світло поширюється прямолінійно, тобто         х = ct, де с - швидкість світла у вакуумі (с = 3·10⁸ м/с).

Маємо: t  c  4,6 (c).

Відповідь: 4,6 с.

Приклад 64. Для освітлення криниці сонячним світлом використали плоске дзеркало. Під яким кутом до горизонту встановили дзеркало, якщо висота Сонця над горизонтом рівна ? 

Розв’язання. При освітленні криниці основну роль грають прямі сонячні промені (мал. 33). Оскільки криниці копають вертикально, то АОТ =^, де ОТ – лінія, паралельна горизонтальній площині; АО – промінь, відбитий дзеркалом ВС. Якщо ON – нормаль до площини дзеркала, а SO – падаючий промінь, то згідно з законом відбивання SON = AON. 

Тоді SOC = AOB, оскільки вони доповнюють кути падіння і відбивання до прямих. З іншого боку, AOB = COD як вертикальні. З малюнка також видно, що SOC = x -  і COD ^ (TOD – прямий). Тоді: x -  =  , або  .

Приклад 65. Промінь світла падає на скляну            (n = 1,5) пластинку так, що заломлений і відбитий промені взаємно перпендикулярні. Визначити кут падіння.

Розв’язування. Оскільки заломлений і відбитий промені взаємно перпендикулярні (мал. 34), то з

урахуванням закону відбивання: NAO + OAT + TAR = , або  ^           Звідси отримуємо зв’язок між кутом падіння  і кутом заломлення  :      

  = ^- .



За законом заломлення  = n. Тоді: tg  = n, тобто  = arctg n =

 

arctg 1,5 = 56.

Відповідь:  = 56.

Приклад 66. Тонка збірна лінза дає на екрані дійсне чітке зображення предмета. Відстань предмета від екрану 2 м, а від лінзи 0,6 м. Визначити фокусну відстань лінзи.

Розв’язання. Оскільки зображення на екрані дійсне і відстань від предмета до лінзи менша, ніж від зображення до лінзи, то умові задачі відповідає мал. 35. Розглянувши подібні трикутники ASF i OBF, а також трикутники ASO i A'S'O, запишемо: .

Враховуючи, що відстань від предмета до екрану L = a + b, маємо:

                   F 0,42 (м).

Відповідь: F = 0,42 м.

Приклад 67. В дно озера вбита свая висотою 4 м, яка виступає з води на  1 м. Визначити довжину тіні сваї на дні озера, якщо сонячні промені падають під кутом 45, а показник заломлення води рівний 1,33.

Розв’язання. Виконаємо малюнок (мал. 36) за умовою задачі. Довжина  тіні складається з двох відрізків: L₁ і L₂. З трикутника АВС маємо: L₁ = h tg.

З трикутника CDF: L₂ = (H - h) tg  .

Кут   визначимо з закону заломлення: ^ n. 



Звідси: . Обчислення дають   = 32. Тоді L = L₁ + L₂ =             h tg + (H - h) tg  .

Обчислимо: L = 1.1+ (4 - 1) 0,625 = 2,875 (м).

Відповідь: L = 2,875 м.

Приклад 68. Показник заломлення алмазу n₁ = 2,42, а скла n₂ = 1,5. Яким повинно бути відношення товщин цих речовин, щоб час поширення світла в них був однаковим?

Розв’язання. Показник заломлення речовини показує, у скільки разів швидкість поширення світла у вакуумі більша, ніж у цій речовині: n,       

n. Тому . 

Звідси:  

1,62. Товщина скла повинна бути в 1,62 рази більшою, ніж

алмазу.

Приклад 69. Визначити головну фокусну віддаль і оптичну силу окулярів, які виправляють недоліки далекозорого ока, для якого віддаль найкращого зору становить 50 см.

Розв’язання. Розглянемо хід променів в окулярній лінзі (мал. 37). Око, озброєне окулярною лінзою, розглядає уявне зображення S' предмета S. Оптична сила лінзи повинна бути підібрана таким чином, щоб це зображення знаходилось на віддалі d

найкращого зору для далекозорого ока, якщо предмет розміщено на віддалі d_o=25 см найкращого зору для нормального ока. 

                   Таким чином: D 2 (дптр).

Відповідь: оптична сила окулярів рівна 2 дптр.

Приклад 70. На поверхню скляного (n₁ = 1,5) об’єктива нанесена тонка плівка, показник заломлення якої n₂ = 1,2. При якій найменшій товщині плівки відбудеться максимальне послаблення відбитого світла в середній частині видимого спектра?

Розв’язання. Умова того, що відбиті від передньої і задньої поверхні плівки хвилі гасять одна одну (для максимального послаблення k = 1) запишеться так: 2h =^ , де ^ – довжина хвилі в плівці, h – товщина плівки. 

В середній частині спектра довжина хвилі  = 0,55 мкм = 5,5·10^-7 м. Таким чином: h .

Відповідь: товщина плівки рівна 1,15 мкм.

Приклад 71. Дифракційна ґратка шириною L = 1 см має N = 2000 штрихів. Яку кількість спектрів утворить вона на екрані необмежених розмірів при опроміненні її світлом рубінового лазера з довжиною хвилі  = 694,3 нм?

Розв’язання. Період ґратки d . Умова максимуму для дифракційної ґратки: k = dsin, де: k – порядок спектру,  - кут дифракції. Значення кута  не може перевищувати 90. Тому при обчисленні кількості спектрів (кількості

максимумів) маємо: k

Відповідь: найбільша кількість спектрів рівна 7.

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Вищий рівень

4.1. Кубічна посудина з непрозорими стінками розміщена так, що око спостерігача не бачить її дна, але повністю бачить стінку CD. Яку кількість води потрібно налити в посудину, щоб спостерігач міг побачити предмет Е (мал. 38), що знаходиться на віддалі 10 см від кута D. Ребро посудини 40 см, показник заломлення води 1,33.

4.2. На яку відстань зміститься промінь, що проходить через плоскопаралельну пластинку товщиною d? Показник заломлення матеріалу пластинки n, а кут падіння променя . Чи може зміщення променя бути більшим від товщини пластинки?

4.3. Зображення предмета на матовому склі фотоапарата з відстані 15 м становить 30 мм, а з відстані 9 м – 51 мм. Знайти фокусну віддаль об’єктива.

4.4. Які окуляри потрібні людині для корекції короткозорості, якщо відстань найкращого зору для неї становить 10 см замість нормальної віддалі  25 см?

4.5. Джерело світла знаходиться на відстані 5 м від екрана. Переміщуючи між ними лінзу, двічі отримали чітке зображення джерела на екрані. Відстань між двома положеннями лінзи, в яких вона давала чітке зображення, складає   10 см. Знайти фокусну віддаль лінзи.

4.6. На розсіювальну лінзу падає збіжний пучок променів. Після проходження через лінзу промені перетинаються в точці, що лежить на віддалі 15 см від лінзи. Якщо лінзу забрати, то точка перетину променів переміститься на 5 см ближче до лінзи. Визначити оптичну силу лінзи.

4.7. На мильну плівку (n = 1,33) падає біле світло під кутом 45. При якій найменшій товщині плівки відбиті промені будуть забарвлені в жовтий            ( = 6·10^-7 м) колір?

4.8. Пучок паралельних променів ( = 700 нм) падає на мильну плівку       (n = 1,33) під кутом 45. При якій найменшій товщині плівки у відбитому світлі спостерігатиметься мінімум?

4.9. Знайти радіус кривизни лінзи, яка використовується для спостереження кілець Ньютона, якщо відстань між другим і третім світлими кільцями 0,5 мм. Установка освітлюється монохроматичним світлом                 ( = 5,5·10^-7 м). Спостереження ведеться у відбитому світлі.

4.10. Визначити довжину хвилі монохроматичного світла, яке падає перпендикулярно на дифракційну ґратку, що має 500 штрихів на 1 мм, якщо кут між максимумами першого і другого порядків становить 20. Оптимальний рівень

4.11. На який кут відхилиться промінь від початкового напряму, впавши на поверхню кварцу (n = 1,54) під кутом 55?

4.12. На якій висоті висить вуличний ліхтар, якщо тінь від вертикальної палиці заввишки 0,9 м має довжину 1,2 м, а коли палицю перемістити на 1 м від ліхтаря вздовж напряму тіні, її довжина стане 1,5 м?

4.13. Промінь світла переходить з води (n₁ = 1,33) у скло (n₂ = 1,5). Кут падіння дорівнює 35. Визначити кут заломлення.

4.14. Граничний кут повного відбивання для деякої речовини на межі з повітрям дорівнює 30. Визначити показник заломлення цієї речовини.

4.15. Промінь падає під кутом 50 на пряму трикутну скляну призму із заломлюючим кутом 60. Визначити кут заломлення при виході з призми.

4.16. Збірна лінза дає уявне і збільшене у 5 разів зображення предмета, віддаленого від лінзи на 4 см. Визначити оптичну силу лінзи.

4.17. Предмет розмістили на відстані 4F від збірної лінзи. Знайти збільшення предмета.

4.18. Відстань від предмета до екрана 3 м. Лінзу якої оптичної сили треба взяти і де треба її розмістити, щоб дістати дійсне зображення предмета, збільшене у 5 разів?

4.19. Відстань між двома сусідніми максимумами інтерференції рівна 1,2 мм. Визначити довжину світлової хвилі, якщо віддаль від джерел до екрану 2 м, а віддаль між когерентними джерелами 1 мм.

4.20. Дифракційна решітка має 120 штрихів на 1 мм. Визначити довжину світлової хвилі монохроматичного світла, що падає на решітку нормально, якщо кут між спектрами першого порядку 8.

Якісні завдання

4.21. Чи справджуватимуться закони відбивання при падінні світла на аркуш паперу? 

4.22. Чому, коли ми сидимо біля багаття, нам здається, що предмети, розташовані по той бік багаття, коливаються?

4.23. Як визначити, яка з двох симетричних двоопуклих скляних лінз однакового діаметра має більшу фокусну відстань?

4.24. Людина наближається до плоского дзеркала з швидкістю v. З якою швидкістю до людини наближається її зображення у дзеркалі?

4.25. Чому не можна використовувати плоске дзеркало, як кіноекран?

4.26. Чому сонячного дня не рекомендується поливати рослини?

4.27. При спостереженні вертикальної мильної плівки можна помітити, що її колір з часом змінюється. Чому?

4.28. Чому для забороняючих сигналів на транспорті використовують червоний колір?

4.29. Для чого весною білять вапном стовбури дерев?

4.30. Відомо, що світло від Сонця надходить до Землі через 8 хв. Чи означає це, що Сонце вже зійшло, а ми починаємо його бачити лише через 8 хв?

          

5. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ

Швидкість світла у вакуумі с не залежить від швидкості руху його джерела й руху приймача світла. Вона є межею швидкостей руху прискорених частинок або передачі якихось сигналів. Лінійка довжиною L_o під час руху відносно спостерігача зі швидкістю v здається коротшою:

                                                               L                                       (5.1)

Під час руху годинника відносно спостерігача його покази подовжуються у відповідності з формулою:

                                                                 t                                         (5.2)

Закон додавання швидкостей двох зустрічних тіл, швидкість кожного з яких v₁ і v₂ має вигляд :

                                                                 v                                            (5.3)

Імпульс частинки масою m₀ в (у стані спокою) збільшується при її прискоренні у сучасному прискорювачі згідно з формулою:

                                                             p 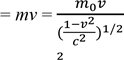                                   (5.4)

                   Енергія Е визначається, як Е                                            (5.5)

де m₀ - маса спокою частинки, v – швидкість її руху відносно спостерігача. Величину m₀с² називають енергією спокою частинки. Маса m є функцією швидкості руху згідно співвідношення m   (5.6)

тоді формула для енергії частинки набуває більш компактного вигляду:

                                                             Е = mс².                                            (5.7)

 

Приклади розв’язування задач

Приклад 72. У космічних променях зустрічаються протони з енергією порядку 10 ГеВ. Якщо діаметр Галактики рівний 10 світлових років, то скільки часу потрібно протону, щоб пройти через Галактику: з точки зору спостерігача, зв’язаного з Галактикою, і «з точки зору протона»?

Розв’язання. Позначимо масу протона (в енергетичних одиницях) через Е_о, а час в системі, зв’язаній з спостерігачем – через t, і «власний» час протона

через t_о. Тоді: Е_к/Е_о  

Так як m_oc² = 1 ГеВ, то нехтуючи цією величиною в порівнянні з енергією протона 10¹⁰ ГеВ, знаходимо, що .

Поряд з цим, відношення  також рівне , тому .

З точки зору спостерігача, зв’язаного з Галактикою, швидкість протона лише незначно відрізняється від швидкості світла, і тому протону для проходження Галактики потрібно затратити стільки ж часу, як і фотону, тобто 10⁵ років. Однак, в системі, зв’язаній з протоном, час протікає повільніше в 10¹⁰ разів. Тому протону для для проходження Галактики потрібен час                 t_o  років = 5 хв.

Відповідь: Для спостерігача, пов’язаного з Галактикою, потрібно 10⁵ років; для спостерігача, пов’язаного з рухомим протоном – всього 5 хв.

Приклад 73. Протон рухається з швидкістю 0,7с. Знайти його імпульс і кінетичну енергію.

Розв’язання. Запишемо вираз для релятивістського імпульсу і врахуємо, що v=0,7c. Отримаємо: р 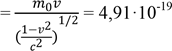(кг м/с). 

Обчислимо кінетичну енергію протона: Е_к .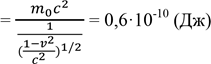

Відповідь: р = 4,91·10^-19 кг м/с ; Е_к = 0,6·10^-10 Дж.

Приклад 74. Яка швидкість руху стержня, якщо його поздовжнє скорочення становить 10% власної довжини?

Розв’язання. Використаємо формулу зміни лінійних розмірів в залежності від швидкості руху: L . За умовою задачі L = 0,9 L_o. Тобто    

9. Звідси знаходимо, що швидкість руху стержня v = 0,436c. Відповідь: швидкість руху стержня рівня 0,436 швидкості світла.

Приклад 75. Якій зміні маси відповідає зміна енергії на 4,19 Дж?

Розв’язання. Зміну маси можна визначити з виразу: m ^

4,75·10^-17 (кг).

Відповідь: m = 4,75·10^-17 кг.

Приклад 76. При якій швидкості руху кінетична енергія будь-якої елементарної частки рівна її енергії спокою?

Розв’язання. Запишемо вираз для кінетичної енергії: E_к = mc² - m_oc² = m_oc².

Тобто: m = 2m_o. Звідси: .

Знаходимо, що v = 0,866 c.

Відповідь: v = 0,866 c. 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

5.1. Яка швидкість руху електрона, якщо його маса перевищує масу спокою в 40000 разів?

5.2. Яка енергія виділяється при повному перетворенні 1 г речовини у випромінювання?

5.3. З якою швидкістю має летіти протон (m_о = 1 а.о.м.), щоб його маса була рівною масі спокою  – частки (m_о = 4 а.о.м.)?

5.4. Сонце випромінює в простір щосекунди близько 3,75·10²⁶ Дж енергії.

На скільки у зв’язку з цим щосекунди зменшується його маса?

5.5. Визначити кінетичну енергію електрона (в МеВ), який рухається з швидкістю 0,6 с.

5.6. Хлопчик, маса якого 45 кг, піднявся сходами будинку на висоту 20 м. На скільки змінилась його маса?

5.7. Яку масу має протон (в а.о.м.), що летить з швидкістю 2,4·10⁸ м/с? Вважати масу спокою протона рівною 1 а.о.м.

5.8. У чайник налили 2 л води і нагріли її від 10 С до кипіння. На скільки змінилась маса води?

5.9. Електрон і протон рухаються назустріч один одному відносно нерухомого спостерігача з швидкостями відповідно 2·10⁸ і 2,5·10⁸ м/с. Знайти швидкості цих часток одна відносно одної, виходячи з релятивістської і класичної формул додавання швидкостей.

5.10. Знайти енергію гама-випромінювання, що виникає при анігіляції електрона і позитрона.

          

6. КВАНТОВА ФІЗИКА

               Енергія кванта світла: E = h =,                                                    (6.1)



де: h = 6,65·10^-34 Дж·с – стала Планка,  - частота фотона,  - довжина хвилі, с – швидкість світла у вакуумі.

                   Імпульс фотона: p                                                                 (6.2)

 

                Маса фотона: m                                                                                  (6.3)



                Формула Ейнштейна для фотоефекту: E ,                           (6.4)

де: А – робота виходу електрона з металу; m – маса електрона; v - максимальна швидкість фотоелектрона.

Фотоефект починається за умови E  A, мінімальна частота світла _min, при якій можливий фотоефект, називається «червоною» межею фотоефекту.

При цьому h_min = A                                                                                     (6.5)

Постулати Бора:

1.                 Атом може перебувати лише в особливих стаціонарних станах, у яких він не випромінює і не поглинає енергії. Кожному стану відповідає певна енергія. Момент кількості руху електрона може приймати значення:

                                                               mvr ,                                              (6.6)

де: m і v – маса і швидкість електрона відповідно; r - радіус електронної орбіти, h - стала Планка, n = 1, 2, 3, … - головне квантове число.

2.                 Світло випромінюється при переході атома з одного стаціонарного стану до іншого. Енергія фотона, що випромінюється, дорівнює різниці енергій стаціонарних станів, між якими відбувається перехід:

 h = E_m - E_n,  (6.7) де: E_m, E_n - енергії стаціонарних станів.

Для атома водню можливі такі частоти електромагнітного випромінювання: 

                                                            ),                                       (6.8)

де: R - стала Рідберга, k₂ - номер електронного рівня, з якого відбувається перехід електрона, k₁ - номер енергетичного рівня, на який переходить електрон при випромінюванні кванта.

Частоти квантів у спектральній серії Бальмера:

          )      (6.9) Приклади розв’язання задач

Приклад 77. Яка частина атомів водню перейде у збуджений стан під дією імпульсу світла з енергією W = 100 Дж і довжиною хвилі  = 0,12 мкм, якщо маса водню m = 100 г? Розв’язання. Кількість фотонів, що мають енергію E= в імпульсі світла



буде: N .

Кількість атомів водню N, де: М = 1 г/моль – атомна маса водню, N_A – число Авогадро. 

Враховуючи, що кожен фотон може збудити лише один атом водню, маємо: .

Відповідь: імпульс світла збудить 1·10^-6 атомів водню.

Приклад 78. У скільки разів змінюється швидкість електрона в атомі водню при переході з другої орбіти на третю?

Розв’язання. Враховуючи формулу Бальмера маємо, що кінетична енергія електрона W .

2hR Або: . Звідки для орбіти з номером k маємо: ^{v } k_2m .

Відношення швидкостей буде:  

Відповідь: швидкість зменшиться у 2,25 рази. 

Приклад 79. У скільки разів кінетична енергія електрона на першій орбіті атома водню відрізняється від його кінетичної енергії на п’ятій орбіті?

Розв’язання. Кінетична енергія електрона W_к в атомі водню дорівнює за абсолютною величиною його повній енергії. Це випливає з таких міркувань. Енергія електрона в атомі: W , де: m i v – маса і швидкість

електрона; r – радіус орбіти; _o – діелектрична стала. За третім законом

Ньютона: , кінетична енергія: , тобто, кінетична енергія електрона в атомі водню дорівнює за абсолютною величиною половині потенціальної або повній енергії: W .

За формулою Бальмера W .

Тобто і W_к . Відношення кінетичних енергій електрона на орбітах з  

k

Відповідь: На першій орбіті кінетична енергія у 25 разів більша, ніж на п’ятій.

Приклад 80. Знайти максимальну швидкість фотоелектронів, що вибиваються з цинку випромінюванням рентгенівської трубки, яка працює при напрузі U = 20 кВ. Робота А виходу електронів з цинку дорівнює 3,7 еВ.

Розв’язання. Максимальна енергія фотона, що випромінюється рентгенівською трубкою, дорівнює енергії eU електрона в трубці. З рівняння

Ейнштейна для фотоефекту маємо: .

Оскільки А = 3,7 еВ значно менша, ніж енергія фотона (eU = 20 кeВ), то величиною А можна знехтувати. Тоді:

7

v  8,4  10 (м / с)

Відповідь: швидкість фотоелектрона рівна 8,4·10⁷ м/с.

Приклад 81. До якого потенціалу зарядиться мідна кулька у вакуумі, якщо її опромінювати світлом частотою  = 1,3·10¹⁶ Гц. Робота виходу електронів з міді А = 4,5 еВ.

Розв’язання. З рівняння Ейнштейна для фотоефекту маємо, що максимальна енергія фотоелектрона: W = h - A.

Коли потенціал  кульки стане таким, що е = W = h - A, то всі електрони, які вириваються з кульки, будуть повертатись назад під дією її електричного поля. Отже:  .

Відповідь: кулька зарядиться до потенціалу 0,83 В.

Приклад 82. Світло, що нормально падає на дзеркальну поверхню, створює тиск р = 10 мкПа. Знайти енергію світла, що падає на S = 1 м² площі поверхні за час t = 1 с.

Розв’язання. За означенням P , де F – нормальна складова сили, що діє на поверхню площею S. З іншого боку: F , де p' – нормальна складова

імпульсу, що передається поверхні за час t. При дзеркальному відбиванні світла імпульс p_f кожного фотона  змінюється на протилежний, тому: p' = 2p_fN, де N – кількість фотонів, що падають на поверхню протягом часу t. Звідси: P .

Енергія фотона E_f і його імпульс пов’язані між собою як p_f , де с – швидкість світла. Враховуючи, що величина E_fN є повною світловою енергією W, що падає на поверхню, маємо:

P . Звідси: W .

Відповідь: енергія світла рівна 1500 Дж. 

Приклад 83. Знайти сталу Рідберга R, якщо найбільша довжина хвилі у спектральній серії Бальмера атома водню дорівнює 0,68 мкм. Розв’язання. Скористаємось формулою Бальмера:  



Довжина хвилі буде найбільшою при k = 3. Звідси:

R  

Відповідь: R = 1,1·10⁷ м^-1. 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

6.1. Джерело світла, потужність якого 100 Вт, випускає 5·10²⁰ фотонів щосекунди. Обчислити середню довжину хвилі випромінювання.

6.2. Під якою напругою працює рентгенівська трубка, якщо найкоротші промені в спектрі трубки мають частоту 10¹⁹ Гц?

6.3. Рентгенівська трубка, що працює під напругою 50 кВ і при струмі      2 мА, випромінює 5·10¹⁸ фотонів щосекунди. Вважаючи, що середня довжина хвилі випромінювання становить 0,1 нм, визначити ККД трубки.

6.4. Якої довжини промені світла треба спрямувати на поверхню цезію, щоб швидкість фотоелектронів становила 2000 км/с? Червона межа фотоефекту для цезію дорівнює 690 нм.

6.5. Яку гальмуючу напругу потрібно подати на вольфрамову пластину, яка освітлюється світлом з довжиною хвилі 0,1 мкм, щоб не виникав фотоефект? Робота виходу електронів з вольфраму 4,5 еВ.

6.6. Знайти енергію фотона для світла, що має довжину хвилі 1 мкм у середовищі з абсолютним показником заломлення, рівним 1,2.

6.7. Фотони частотою 1,5·10¹⁶ Гц виривають електрони з поверхні металу, що має роботу виходу електронів 7,2·10^-19 Дж. Знайти максимальний імпульс, який передається металу в одному акті фотоефекту.

6.8. Знайти довжину хвилі випромінювання, для якого маса фотона дорівнює масі спокою електрона.

6.9. Робота виходу електронів для міді дорівнює 4,47 еВ. Чи буде спостерігатись фотоефект під дією випромінювання з довжиною хвилі          0,42 мкм?

6.10. Які закономірності фотоефекту свідчать про те, що світло поглинається окремими порціями?

6.11. Яку назву має найбільший струм фотоелемента при даному світловому потоку, що падає на фотокатод?

6.12. Ідеальні дзеркальну та чорну поверхні опромінюють світлом в однакових умовах. На яку поверхню світло чинить більший тиск і у скільки разів?

6.13. Чи залежить швидкість фотоелектронів, які вириваються з фотокатода, від його освітленості?

6.14. На якому явищі заснований принцип дії оптичного квантового генератора?

6.15. На плоскопаралельну пластинку під кутом  падає світло. Яким буде напрям прискорення пластинки під дією світла, якщо пластинка: а) поглинає всі фотони; б) дзеркально відбиває їх?

          

7. АТОМНА ФІЗИКА

                   Правило зміщення для  – розпаду:                  (7.1)

                    Правило зміщення для   – розпаду:            (7.2)

де: Х – символ хімічного елемента, якому належить материнське ядро; Y – символ хімічного елемента, якому належить дочірнє ядро; A i Z – масове число і атомний номер хімічного елемента у періодичній системі.

t



                  Закон радіоактивного розпаду: N  N₀ 2 ^T ,                                      (7.3)

де: N_o - число атомів радіоактивної речовини в момент часу t = 0; N - число атомів радіоактивної речовини в момент часу t; Т – період піврозпаду речовини. 

Дефект маси ядра m = Zm_p + (A - Z)m_n - M_z        (7.4) де: m_p - маса протона; m_n - маса нейтрона; M_z – маса ядра.

                Енергія зв’язку ядра: E_зв = m c²                                                        (7.5)

                   Питома енергія зв’язку ядра: Е_пит                                              (7.6)

Енергія,      що     виділяється          або    поглинається       при    ядерній           реакції                 X₁ + Y₁  X₂ + Y₂: W = [m(X₁) + m(Y₁) – m(X₂) - m(Y₂)] c² (7.7) де: X₁, Y₁, X₂, Y₂ – символи хімічних елементів, яким належать реагуючі атомні ядра; m(X₁), m(Y₁), m(X₂), m(Y₂) – маси атомів або відповідних атомних ядер.

Для визначення маси ядра потрібно від маси нейтрального атома відняти сумарну масу його електронів. Якщо величина W позитивна, то енергія в реакції виділяється; якщо ж W негативна – то енергія поглинається.

 

Приклади розв’язування задач

Приклад 84. Вважаючи, що вік Землі і період піврозпаду  приблизно однакові (4,5·10⁹ років) і що весь свинець  в урановій руді утворився при радіоактивних перетвореннях урану, розрахувати, яким повинно бути сучасне співвідношення маси свинцю і маси урану.

Розв’язання. За законом радіоактивного розпаду кількість атомів урану

t



N  N₀ 2 ^T , де: N_o - їх початкова кількість. Якщо t  T, то N.

Кількість атомів свинцю N.

Їх співвідношення  

Відповідь: відношення маси свинцю до маси урану рівне 1.

Приклад 85. Знайти найбільшу швидкість релятивістських   – часток, що виникають при перетворенні нейтрона у протон. Маси часток;                 m_n = 1,675·10^-27 кг, m_p = 1,673·10^-27 кг, m_e = 9·10^-31 кг.

Розв’язання. Електрон набуває найбільшої швидкості, коли енергія нейтрино рівна нулю. При цьому енергія електрона: W=(m_n - m_p - m_e) c² = 9,9·10^-14 (Дж).

З релятивістської формули: W .

_Звідси v  cW W²  me²c⁴  2,8 10⁸(м/ с) .

Відповідь: швидкість електронів рівна 2,8·10⁸ м/с.

Приклад 86. Активність радіоактивної речовини зменшилась у 4 рази протягом 10 діб. Знайти період її піврозпаду.

Розв’язання. Згідно із законом радіоактивного розпаду 0,25 (діб). Звідки Т = 5 діб. 

Відповідь: Т = 5 діб.

Приклад 87. Знайти атомну масу магнію, який має три ізотопи , ,  з процентним вмістом 78,7%, 10,1% і 11,2% відповідно.

Розв’язання. Атомна маса магнію визначається процентним вмістом ізотопів: А (а.о.м.).

Відповідь: атомна маса магнію рівна 24,33 а.о.м.

Приклад 88. Виділяється чи поглинається енергія в реакції +

? Маси атомів у а.о.м.: m 14,0031; m       4,0026; m() = 16,9991; m() = 1,0078.

Розв’язання. Знайдемо різницю суми мас спокою реагуючих часток та суми мас часток-продуктів реакції: m = - 0,0012.

З розрахунку видно, що сумарна маса спокою часток в результаті реакції збільшується. Це свідчить про поглинання енергії.

Відповідь: енергія в реакції поглинається.

Приклад 89. Розрахувати потужність атомної електростанції, яка витрачає 0,2 кг  за добу, якщо ККД станції 16%. Вважати, що при діленні одного ядра урану виділяється 200 МеВ енергії.

Розв’язання. Кількість ядер урану, що ділиться за добу , де: N_A – число Авогадро; М = 0,235 кг/г-атом – атомна маса урану. Енергія, що при цьому виділяється: W = eN 200 (МеВ).

                Потужність станції: P ^ (МВт).

Відповідь: потужність станції 30 МВт.

 

 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

7.1. Яка частина радіоактивних ядер деякого елемента розпадається протягом часу, що дорівнює трьом періодам піврозпаду?

7.2. Атомна маса елемента бора дорівнює 10,8 а.о.м. Він має два ізотопи  і . Знайти їх процентний вміст.

7.3. На скільки змінюється масове число та атомний номер елемента при послідовному випромінюванні  – частки і двох  – квантів?

7.4. Визначити різницю мас  у збудженому та в основному станах, якщо при переході із збудженого стану в основний він випромінює  – квант з енергією 17,2 МеВ.

7.5. Розрахувати енергію зв’язку ядра дейтерію . Маси нуклонів:         m_p = 1,673·10^-27 кг; m_n = 1,675·10^-27 кг; маса ядра дейтерію 3,342·10^-27 кг.

7.6. Знайти енергію, що виділяється при утворенні гелію  масою 1 кг з протонів і нейтронів. Маса ядра гелію 6,643·10^-27 кг; маси нуклонів:                

m_p = 1,673·10^-27 кг; m_n = 1,675·10^-27 кг.

7.7. Написати рівняння реакції, яка відбувається при бомбардуванні бору   – частками і супроводжується вибиванням нейтрона.

7.8. Яка енергія потрібна для розщеплення ядра азоту  на нуклони?

7.9. Яку мінімальну енергію повинна мати  – частка, щоб відбулась ядерна реакція  ?

7.10. Яка енергія виділяється при термоядерній реакції  

 ?

7.11. Чому повільний протон не може викликати ядерну реакцію, а повільний нейтрон може?

7.12. З чим пов’язана необхідність сповільнення швидких нейтронів у ядерних реакторах?

7.13. Чому дорівнює коефіцієнт розмноження нейтронів під час стаціонарного протікання ланцюгової реакції у ядерному реакторі? Як він досягається?

7.14. Розмістіть  -,   - і  – промені в порядку зменшення їх небезпеки при зовнішньому опроміненні людини.

7.15. Чому реакції синтезу легких атомних ядер відбуваються лише при дуже високій температурі реагуючих речовин?

          

ВІДПОВІДІ НА ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

1.1. 55 км/год. 1.2. 121,65 км/год. 1.3. 1500 км. 1.4. v_1c = 48 км/год, v_2c = 50 км/год. 1.5. 155,6 м. 1.6. 15 м/с. 1.7. 13,1 м/с. 1.8. 17,5 км/год. 1.9. 2.5 год.; 150 км від м. А. 1.11. 4,2 хв. 1.12. 150 м. 1.13. 2,25 м/с, 6326. 1.14. 125 с. 2 м/с. 686. 1.15. 10930. 1.16. 135. 9,3 м/с. 1.21. 4,14 м/с. 1.22. 225 м. 5 м/с. 7,5 м/с.

1.23. 1,4 м/с. 14 с. 1.24. 152 м. 1.25. 198 км/год. 1.26.   5 м/с². 39 м/с. 40 м 1.27. 3,53 м/с². 112.9 м. 1.28. 45,5 км/год. 1.29. 10 м/с. 25 с. 1.31. 6,48.105 м/с². 1.32.

52,2 с. 1.33. 13,61 м. 1.34. 66,4 м. 1.35. 6,06 м. 1.36. 20,4 м. 1.37. горизонтально. 1.38. 1,62 с. 1.39. h = 2v_ot . 1.40. 57,08 м; 33,44 м. 1.41. 0,731 с; 3,347 с. 1.42. 3,34 с; 24,75 м/с. 1.43. 6,39 м/с. 1.44. 1,98 м/с. 1.45. 12,28 м/с. 1.46. в два рази.

1.47. 35,84 м/с; 33 до горизонту. 1.48. 210 м/с. 1.49. 14,69 м. 1.50. 28,82 м/с.

1.51. 0,0105 м/с. 1.52. 1,59 об/с; 30 см. 1.53. 305,6 м/с. 1.54. 1,65 оберту. 1.55. 60.

1.61. так. 1.62. 26,46 Н. 1.63. 97,3. 1.64. 5,32 Н. 1.65. 11,88 м/с. 1.66. 1,5 м/с; 0,003. 1.67. так. 1.68. 0,494 м/с2. 1.69. 0,085; 62,5 Н. 1.70. 13,47 т. 1.71. 7,42 м. 1.72. 1160 Дж. 1.73. 1.74. 2,02 м/с2; 9 Н. 1.75. 1 м/с2. 1.76. 3557 Н. 1.77. 0,639

с. 1.78. 2222 Н. 1.79. 5,715 с^-1. 1.80. 12,4 Н. 1.81. 85,6%. 1.82. 12,52 м/с. 1.83. 0,262. 1.84. 3395 Н. 1.85. 5,71 с; 0,1. 1.86. 674,9 Дж. 1.87. 4350 Дж. 1.88. 113,5 кН. 1.89. 60. 1.103. 5,98 см. 1.104. 6,23 м/с. 1.105. x = 0,05 sin(1,57t + /4). 1.106.

15. 1.107. 275,8 Гц. 1.108. 350 м/с. 1.109. /2 рад. 1.110. Т₂ = Т₁(₂/₁)1/2.

2.1. n = kV/V_o. 2.2. 2,83%. 2.3. 100 Дж. 2.4. 250 Дж. 2.5. C_v = 311,6 Дж/кгК.

C_p = 519,4 Дж/кгК. 2.6. 10,34 м. 2.7. 273 С. 2.8. 1,6 рази. 2.9. 26,1 г; 123,9 г. 2.10. 2,57 рази. 2.12. 53,9%. 2.13. А = 12,46 кДж; U = 31,16 кДж; Q = 43,62 кДж.

2.14. 2,81.10^-10 м. 2.15. 1,667 кг/м³. 2.16. 13,9 коп. 2.17. 816,3 кг/м³. 2.18. 8,12 л. 2.19. збільшиться в 1,43 рази. 2.20. Т₂ = 401Т₁/400. 2.21. Р₂/Р₁ = 14. 2.22. 234,7 Дж. 2.23. 23,1%; 46,15 кДж; 13,85 кВт. 2.24. 0,685 Дж. 2.25. 10,62 м³. 2.26. 89,4

С. 2.27. 15,1 мм. 2.28. 0 С; ні. 2.29. 527,5 С. 2.30. 1,189х0,743х0,396 мм³.

3.1. 1,25 r. 3.2. 40 нКл; 10 см від від’ємного заряду. 3.3. 0,0576 Н/Кл; 0,0432 Н/Кл. 3.4. 2а/3 від більшого заряду; а/3 за меншим зарядом. 3.5. 1,5 q/_oa². 3.6. 2. 3.7. 2940. 3.8. 2 рази. 3.9. 4,5.10^-7 Дж. 3.10. 1 мкФ. 3.11. 36 Дж; 15 кВт. 3.12. 10¹¹ електронів. 3.13. 200 В/м. 3.14. 1,6.10^-17 Дж; 5,93.106 м/с. 3.15.

2600 В. 3.16. 2.104 В/м. 3.17. збільшиться в 1,5 рази. 3.18. 8. 3.19. 16 разів. 3.20.

1,09 мкФ; 1,67 мкФ; 2,33 мкФ; 3 мкФ; 4,4 мкФ; 5,5 мкФ; 8,33 мкФ; 12 мкФ. 

3.46. 0,25 мм/с. 3.47. Другий. 3.48. 2,97 А. 3.49. 2/3. 3.50. в 10 разів. 3.51.

20 кОм. 3.52. 0,002 Ом. 3.53. 50 А. 3.54. 53 г. 3.55. 50%. 3.56. 0,2 Ом; 12 В. 3.57. 6 Ом; 33%; 67%. 3.58. Збільшиться в 5 разів; зменшиться у 1,8 рази; збільшиться в 2,8 раза. 3.59. 50 хв. 3.60. 330 кВт·год. 3.61. а) не можна; б) можна. 3.62. 74 С. 3.63. 400 Вт; 200 Вт; 800 Вт. 3.64. 2В; 1,8 В. 3.65. Р₁/Р₂ = 9. 

3.66. 6,2 Ом. 3.77. а) для  – частки в 2 рази більше; б) однакові. 3.78. 20 мТл. 3.79. B = (mgtg)/IL. 3.80. 1000 км/с. 3.81. 100.  3.82. 2,5 Дж. 3.83. 5А. 3.84. 50 мТл. 3.85. 0,32 пН. 3.86. 8,9 нс.  3.87. 0,2 Вб. 3.88. 100 В. 3.89. 120 Дж. 3.90. 5,8 м/с. 3.101. Т/2. 3.102. C=1/4_²L. 3.103. 100. 3.104. Q = (3CUm²)/8 = 0,6 Дж.

3.105. 120 мкДж. 40 мкДж. 3.106. 710 кГц; 71 МГц. 3.107. 2 кГц. 3.108. 1/3; 2550; у первинній. 3.109. 20 В. 3.110. 5.104. 

4.1. 43,2 л. 4.2. x=d sin( -  )/cos , де   – кут заломлення. x = x_max = d при

 = 90. Не може перевищувати товщину пластинки. 4.3. 0,43 м. 4.4. – 6 дптр. 4.5. 0,12 м. 4.6. – 3,3 дптр. 4.7. 0,13·10^-8м. 4.8. 0,15 мм. 4.9. 5,7 м. 4.10. 0,6·10^-6 м. 4.11. 23. 4.12. 3,9 м. 4.13. 28. 4.14. 2 4.15. 56 4.16. 20 дптр. 4.17. 3 рази. 4.18.

2,4 дптр; 0,5 м.  4.19. 600 нм. 4.20. 580 нм. 

5.1. 0,999 с. 5.2. 9.1013 Дж. 5.3. 0,97 с. 5.4. 4,2.106 т.  5.5. 0,13 МеВ. 5.6. Збільшилась на 10^-13 кг. 5.7. 1,7 а.о.м. 5.8. 8,4.10^-12 кг. 5.9. v_p=2,6.10⁸ м/с; v_кл > c, що неможливо.  5.10. 1,02 МеВ.  

6.1. 0,99 мкм. 6.2. 41 кВ. 6.3. 0,1%. 6.4. 94 нм. 6.5. 7,9 В. 6.6. 0,04%. 6.7.

7.10^-25 кгм/с. 6.8. 2,4.10^-12 м. 6.9. _ч = 0,28 мкм; фотоефекту не буде. 

7.1. 7/8. 7.2. 80%, 20%. 7.3. А зменшується на 4 одиниці, Z зменшується на

2 одиниці. 7.4. 3,1.10^-29 кг. 7.5. 5,4.10^-13 Дж. 7.6. 7,2.10¹¹ Дж. 7.8. 10⁵ МеВ.  7.9. 2,8 МеВ. 7.10. 18 МеВ.

          

Додаток 1

ОСНОВНІ ФОРМУЛИ

          

    

    

    

    

    

Додаток 2

Густина речовини

 

 

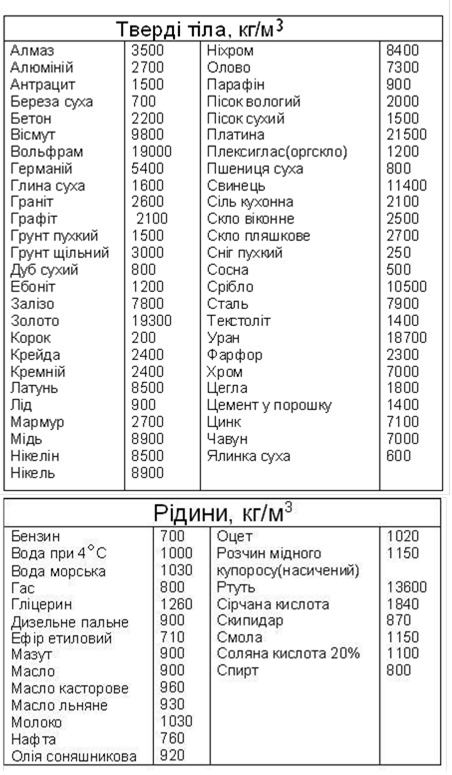
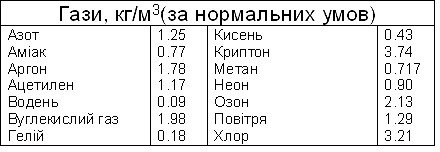
Питома теплоємність речовини

 

      

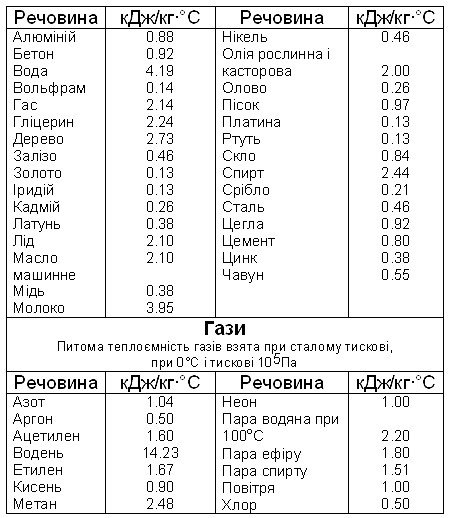
Температура плавлення і кристалізації

 

 

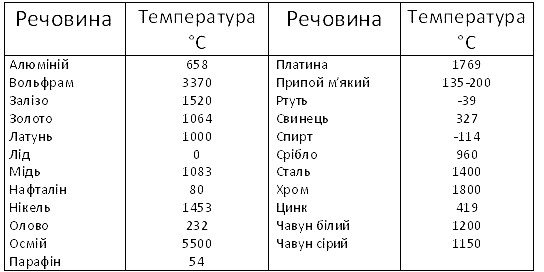
Питома теплота плавлення і кристалізації

 

 

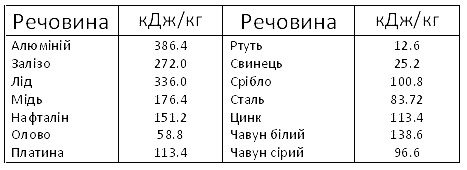
Температура кипіння

 

 

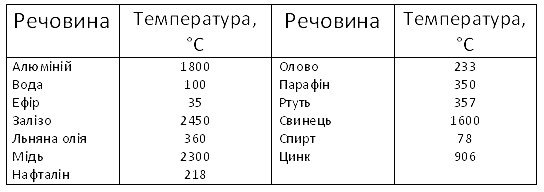
Питома теплота пароутворення

 

 

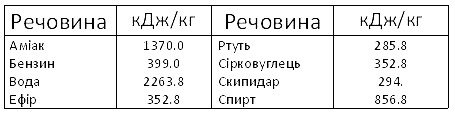
Питома теплота згоряння палива

 

 

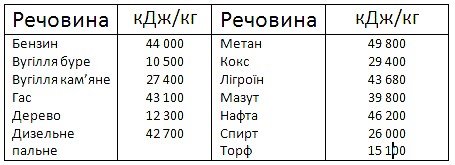
Діелектрична проникність

 

 

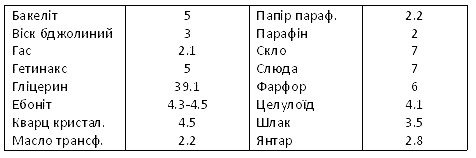
Питомий опір

 

         

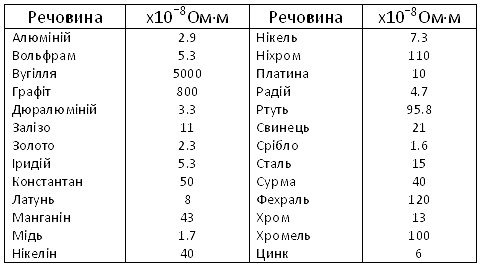
Температурний коефіцієнт опору

 

 

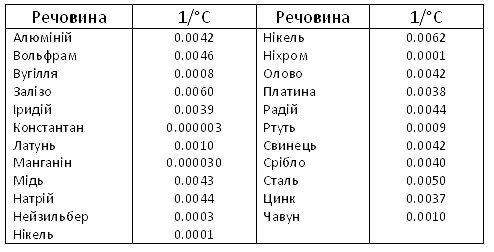
Фізичні сталі

        

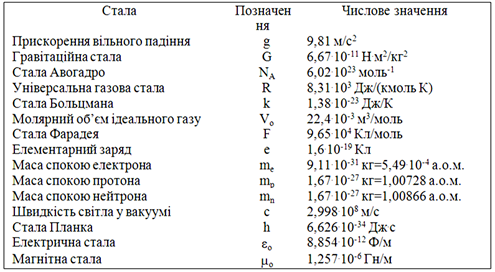
Періодична система хімічних елементів

 

Таблиця синусів і тангенсів кутів

 

           

ВИКОРИСТАНА ЛІТЕРАТУРА

1.          Коршак Є.В., Ляшенко О.І., Савченко В.Ф. Фізика 9 клас. Підручник для загальноосвітніх навчальних закладів. – К.: Генеза, 2009.

2.          Генденштейн Л.Е. Фізика. 9 клас: Навчальний посібник. – Х.: Гімназія, 2000.

3.          Бар’яхтар В.Г., Божинова Ф.Я., Кірюхін М.М., Кірюхін О.О. Фізика. 11 клас. Академічний рівень. Профільний рівень: Підручник для загальноосвітніх навчальних закладів. – Х.: Ранок, 2011.

4.          Бар’яхтар В.Г., Божинова Ф.Я. Фізика. 10 клас. Академічний рівень: Підручник для загальноосвітніх навчальних закладів. – Х.: Ранок, 2011.

5.          Римкевич А.П. Збірник задач з фізики 9 – 11 класів середньої школи. – К.: Рад. школа, 1991.

6.          Гольдфарб Н.І. Збірник запитань і задач з фізики. Посібник для підготовчих відділень. – К.: Вища школа, 1986.

7.          Гельфгат І.М., Гендештейн Л.Е., Кирик Л.А. 1001 задача з фізики з відповідями, вказівками, розв’язаннями. – Х.: Гімназія, 1998.

8.          Гельфгат І.М., Ненашев І.Ю. Фізика. Збірник задач 9. – Х.: Гімназія, 2002. 9. Вознюк С.Ю. Практикум з розв’язування задач з елементарної фізики. Теплові явища: Посібник для учнів, студентів та вчителів. – Тернопіль: Підручники і посібники, 1998.

10.      Вознюк С., Дубас З. Дидактичні матеріали з фізики. 11 клас. – Тернопіль: Підручники і посібники, 2001.

11.      Корсак К.В. Збірник запитань та якісних завдань з механіки: Посібник для вчителів. – К.: Рад. школа 1988.

12.      Пістун П. Збірник задач з фізики. 11 клас. – Тернопіль: Підручники і посібники. 2004.

 

 

 

 

 

 

 

Теличко І.І.

Фізика: готуємося до ЗНО

Навчальний посібник