Посібник "Усний рахунок"





Автор :
С.В. Пазиненко , учитель математики Горішньоплавнівської ЗОШ І-ІІІ ступенів №6
Рецензент:
В.О. Єрмачкова , учитель математики Комсомольської ЗОШ І-ІІІ ступенів №6
Методичний посібник розроблений для вчителів математики 5 – 6 класів.

Розвиток у дітей логічного мислення – це одна з важливих задач навчання. Уміння мислити логічно, робити висновки без наочної опори, співставляти судження за визначеними правилами – необхідна умова успішного засвоєння навчального матеріалу. В будь-якій задачі закладені великі можливості для розвитку логічного мислення. Нестандартні логічні задачі – відмінний інструмент для такого розвитку. Використання на уроках математики і позаурочних заняттях спеціальних задач і завдань, спрямованих на розвиток логічного мислення, розширює математичний кругозір і дозволяє більш впевнено орієнтуватися в найпростіших закономірностях навколишньої дійсності й активніше використовувати математичні знання в повсякденному житті.
"Головна задача навчання математиці, причому із самого початку, з першого класу, - учити міркувати, учити мислити", - писав педагог-новатор А.А. Столяр.
Найважливішим завданням математичної освіти є озброєння учнів загальними прийомами мислення, просторової уяви, розвиток здатності розуміти зміст поставленої задачі, уміння логічно міркувати, засвоїти навички алгоритмічного мислення. Кожному важливо навчитися аналізувати, відрізняти гіпотезу від факту, чітко виражати свої думки, а з іншого боку - розвити уяву й інтуїцію (просторове представлення, здатність передбачати результат і угадати шлях розв’язання ). Саме математика надає сприятливі можливості для виховання волі, працьовитості, наполегливості в подоланні труднощів, завзятості в досягненні мети.

Однією із основних задач викладання курсу математики в сучасній середній школі є формування в учнів свідомих та міцних обчислювальних навичок.
Обчислювальна культура формується в учнів на всіх етапах вивчення курсу математики, але основа її закладається у перші 5-6 років навчання.
Одним з найважливіших засобів інтенсифікації навчання математиці є впровадження ефективної систематизації навчального матеріалу для усного обчислення.
До усного опитування доцільно вдаватися майже на кожному уроці: у процесі перевірки домашнього завдання, активізації знань за новим матеріалом, при фронтальному опитуванні, плановому тематичному обліку знань. Вдало підібрані і систематично виконувані усні вправи сприяють розвиткові логічного мислення учнів, підвищують їх математичну культуру, формують важливі навички тотожних перетворень, збуджують творчу активність, привчають до зосередженості.
Оволодіння навичками усних обчислень корисно ще і тому, що вони прискорюють письмові обчислення, дозволяють вдосконалювати їх. Наявність в учнів навичок усних обчислювань впливає на степінь набування в них раціональних та безпомилкових обчислювальних вмінь.
У даному посібнику розроблені вправи для усного рахунку.
Усні вправи, вміщені у посібник, я поділяю на такі види:
- Умова вправи сприймається учнями на слух, і після усного її розв’язування вони, нічого не записуючи, повідомляють знайдений результат.
- Учні читають умову вправи, а розв’язування виконують усно.
- Учні, розглянувши малюнок і короткий запис умови геометричної задачі, усно знаходять відповідь.
- За умовою задачі учень створює відповідний малюнок геометричної фігури, розв’язування виконується без записів.
Мета посібника: поділитися з колегами власним досвідом активного використання усних вправ у процесі навчання учнів математики; привернути увагу до цієї форми роботи з дітьми, оскільки вважаю її необхідною і ефективною.

-
 Обчислити усно:
Обчислити усно:

- Обчислити усно:

- Обчислити усно:
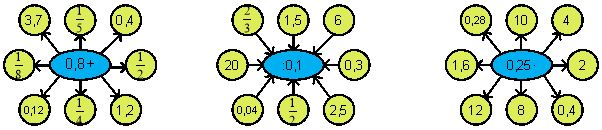
- Обчислити усно:

- Яке число пот рібно вписати в порожню клітинку ланцюжка:

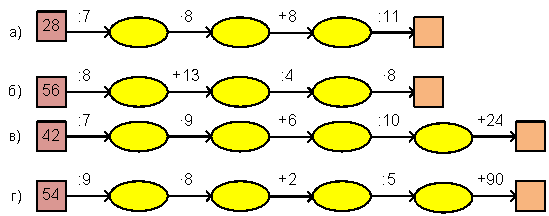
- Яке число потрібно вписати в порожню клітинку ланцюжка?

- Дізнайся назву професії. Що ти про неї знаєш?
|
8 |
|
|
21 |
|
|
14 |
|
|
9 |
|
|
+9 ·3 -2 :7 |
|
-15 ·6 :4 +25 |
|
+18 :8 ·15 -37 |
|
·12 -9 :11 +6 |
|
|||
|
|
Ч |
|
Р |
|
А |
|
Л |
|
72 |
|
|
18 |
|
|
54 |
|
|
7 |
|
|
-48 :3 ·7 +14 |
|
·8 +6 :3 -26 |
|
:9 ·14 :21 ·7 |
|
+8 ·10 -110 :5 |
|
|||
|
|
Д |
|
Е |
|
К |
|
П |
|
8 |
24 |
34 |
24 |
28 |
15 |
23 |
70 |
23 |
7 |
|
|
|
|
|
|
|
|
|
|
|
8.Розшифруй слово.
|
210 |
|
|
340 |
|
|
600 |
|
|
480 |
|
|
92 |
|
|
300 |
|
|||||
|
:7 :5 ·17 -49 +8 |
|
+80 :14 ·5 -70 :16 |
|
-40 :2 ·3 +60 :18 |
|
:60 +15 ·9 -47 :4 |
|
-85 ·70 +50 :60 +37 |
|
:25 ·7 +16 -19 :9 |
|
||||||||||
|
|
Й |
|
|
У |
|
Е |
|
З |
|
І |
|
В |
|||||||||
|
9 |
50 |
40 |
5 |
9 |
46 |
61 |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
9.Обчисли усно:
|
:2 +38 :15 ·9 |
|
47+25 :36 ·19 -6 :4 |
|
14+49 :3 19 :8 ·16 |
|
7·5 ·3 -9 :16 ·7 |
|
|
|
|
|
|
45:3 ·5 -19 :8 ·17 |
|
20·8 :40 ·27 -27 :9 |
|
90-26 :8 ·60 -30 :9 |
|
80·9 -90 :70 ·6 :18 |
|
|
|
|
|
10.Обчисли та розташуй отримані числа в порядку зростання. У відповіді – им’я математика 18ст.,який відкрив визначну закономірність , пов’язану з поняттям простого числа.
|
19 |
|
|
56 |
|
|
350 |
|
|
340 |
|
|
490 |
|
|
·4 -22 :6 ·8 :12 |
|
-49 ·9 +45 :36 ·34 |
|
:5 +25 :19 ·20 -28 |
|
+160 :20 -9 ·7 :14 |
|
:7 ·4 :10 -19 ·9 |
|
||||
|
|
О |
|
Х |
|
Д |
|
Л |
|
Б |


|
34 |
|
|
92 |
|
|
900 |
|
|
+56 :5 ·7 -27 :11 |
|
-17 :5 +19 ·3 -12 |
|
-260 :80 ·60 :12 -37 |
|
||
|
|
Ь |
|
А |
|
Г |
11.Обчисли усно
|
6+9= |
|
7+8= |
|
9+5= |
|
2·9= |
3·4= |
5·6= |
||
|
20-3= |
20-4= |
20-5= |
||
|
54:9= |
49:7= |
48:6= |
||
|
13-5= |
12-7= |
11-7= |
||
|
50·5= |
9·30= |
40·7= |
||
|
42+8= |
53+7= |
15+5= |
||
|
160:2= |
240:6= |
180:3= |
||
|
50+60= |
50+70= |
50+80= |
||
|
14·5= |
13·3= |
15·7= |
||
|
32+11= |
32+12= |
32+13= |
||
|
63:3= |
88:4= |
46:2= |
||
|
46+8= |
32+9= |
25+7= |
||
|
30:15= |
36:18= |
38:19= |
|
|
|
6+7= |
|
5+6= |
|
8·3= |
7·2= |
4·4= |
||
|
20-6= |
20-7= |
20-8= |
||
|
81:9= |
63:7= |
36:9= |
||
|
15-9= |
14-6= |
16-7= |
||
|
6·60= |
80:4= |
70·8= |
||
|
31+9= |
47+3= |
26+4= |
||
|
450:5= |
640:8= |
150:3= |
||
|
50+90= |
70+30= |
80+30= |
||
|
18·5= |
19·2= |
18·4= |
||
|
32+14= |
32+15= |
32+16= |
||
|
39:3= |
52:4= |
72:2= |
||
|
56+8= |
69+3= |
28+5= |
||
|
54:27= |
28:14= |
64:32= |
12.Обчисли усно:
|
248+32 |
|
700:14 |
|
6-2,8 |
|
1:4 |
|
3,8:19 |
|
4,7+1,3 |
|
:40 |
·9 |
:4 |
-0,2 |
·24 |
:0,1 |
|||||
|
·60 |
-70 |
·3 |
·8 |
:3 |
·0,25 |
|||||
|
-90 |
:20 |
+0,8 |
+0,35 |
+5,4 |
:50 |
|||||
|
:33 |
+6 |
:3,2 |
:0,3 |
:70 |
-0,05 |
|||||
|
? |
? |
? |
? |
? |
? |

13.Обчисли усно та знайти добуток отриманих чисел найбільш зручним способом:
|
3,6·0,5 |
|
0,6:0,03 |
|
6-1,8 |
|
1,5+3,6 |
|
10:0,4 |
|
:0,6 |
|
-12 |
|
:7 |
|
:3 |
|
-0,9 |
|
·80 |
|
·0,9 |
|
+0,8 |
|
-0,1 |
|
·3 |
|
+260 |
|
+2,6 |
|
·5 |
|
:0,04 |
|
:48 |
|
·0,1 |
|
·0,1 |
|
-4,5 |
|
·10 |
|
-0,08 |
|
? |
|
? |
|
? |
|
? |
|
? |
14. Виконай дії за схемою:

15.Обчисли усно:
|
|
|
|


|
-7 |
|
|
-12 |
|
|
-3 |
|
|
2,8 |
|
|
-2,4 |
|
|
:0,1 +40 ·0,09 -1,6 |
|
·10 +270 :(-30) +1,6 |
|
:(-4) +0,15 ·(-2) -0,7 |
|
+5,2 :0,2 -50 +8,4 |
|
·0,5 +4 ·(-0,1) :0,4 |
|
||||
|
|
? |
|
? |
|
? |
|
? |
|
? |
:
16.Розташуй відповіді прикладів в порядку зростання і ти дізнаєшся як у стародавні часи називали рифму :
|
С |
12·3 |
|
Г |
216:4 |
|
Є |
750:25 |
|
С |
27·4 |
А |
480:40 |
О |
520:13 |
||
|
Є |
38·70 |
А |
204:3 |
К |
600:150 |
||
|
І |
490·3 |
Л |
280:5 |
Р |
840:140 |
17.Розвяжи приклади:
|
а) |
50+40 :30 ·50 -100 |
б) |
30+70 :10 ·15 -150 |
в) |
100-70 ·3 -18 :36 |
г) |
100-80 :4 ·14 -67 |
д) |
67-23 :11 ·25 -19 |
|
? |
? |
? |
? |
? |


18.Клоун пропонує глядачам пограти з ним в гру . Він називає натуральне число. Хтось з глядачів називає ще більше натуральне число. Потім клоун називає ще більше число, глядач ще більше і т.д. Виграє той, хто назве число, більше якого ніяких натуральних чисел немає. Чи може хтось взагалі виграти в цій грі ? Поясніть.
19. Клоун зашифрував букви таким чином :
|
букви |
А |
Б |
В |
Г |
Д |
Е |
Ї |
Ж |
З |
К |
О |
Ч |
І |
|
шифр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
і розказав глядачам таку “секретну” казку: “Жили – були 5 13 5 і 2121.На дворі в них жили 781 12 11 10 і 8121. Приходить якось 2121 і схвильовано говорить : “2 13 51 ! Я бачу тільки 781 12 10 1 Ти не знаєш 56 8121 ?” 5 13 5 відповідає : “51 , знаю . Вона у 319 13. Але 8 там була морська 936951 ! 56 вона ?” “Я подарував 77 онучці 19 13”
Розшифруйте казку.
Зашифруйте такі слова : “ваза” , “газ” , “діва” , “їжа”.
20. Обчислити усно:

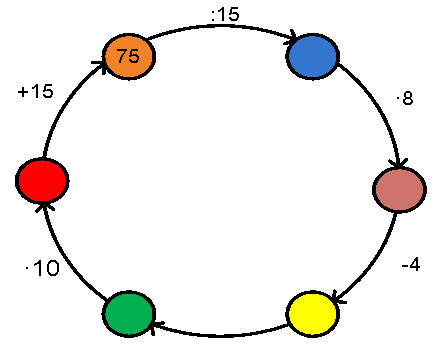
21. Відновити ланцюжок обчислень:
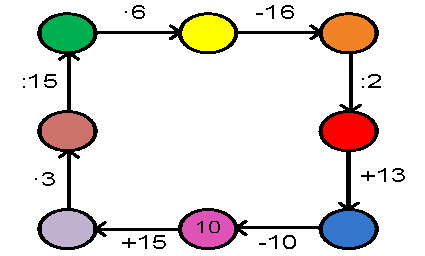
22.
|
|
Клоун казав публіці: «За останній тиждень я став набагато товстіший. Важив усього 79 год. і став важче на три гривні. Уявляєте, скільки я зараз важу? (Замініть назви одиниць і скажіть, скільки важить клоун?)
|
23. Обчислити усно:
|
|
50·2 -58 :14 +21 :12 |
б) |
32+58 :6 -2 ·5 +35 |
в) |
32+25 :5 -9 ·16 +12 |
г) |
6·12 +28 :10 -6 ·15 |
д) |
32:16 ·25 +34 :12 ·10 |
|
? |
? |
? |
? |
? |
24. Відновити ланцюжок обчислень:
25. Знайти значення числових виразів, не підраховуючи суми у кожному із них:
3+5-5 28+47-28 72356803 + 96873544 - 96873544
3+5-3 28+47-47 10001000010 + 22222222222 – 10001000010
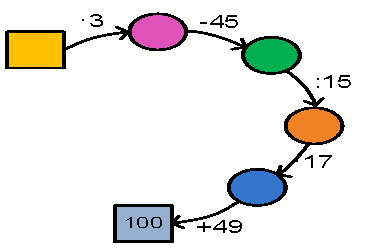
26. Відновити ланцюжок обчислень:
27. Обчислити усно:
|
а) |
53-46 ·7 +31 -45 :7 |
б) |
63-57 ·6 +34 -30 :8 |
в) |
81-73 ·8 +26 -58 :8 |
г) |
520+280 :20 ·5 :25 ·125 |
д) |
600-120 :4 ·2 :5 ·20 |

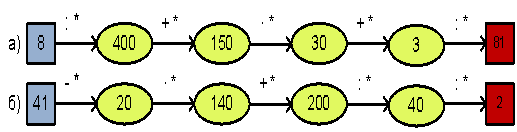
26. Відновити ланцюжок обчислень:

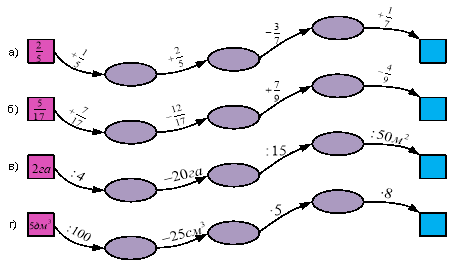
27. Знайти закономірність. Заповнити кружечок:
28. Сума ніг дає те число, що і множення хвоста самого на себе:

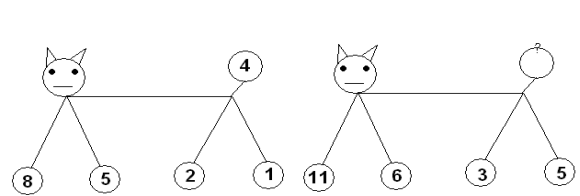
29. Обчислити усно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30. Відновити ланцюжок обчислень:
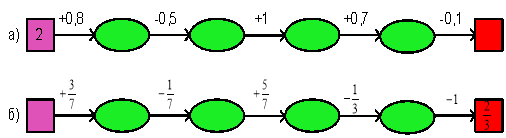
31. Обчислити усно:
|
|
92:27 ·32 +14 :10 -11 |
б) |
53·8 :20 -49 ·80 :5 |
в) |
1ч 20мин :4 -15мин :100 +7с |
г) |
2га 10а :7 +15а :500 -9м2 |
д) |
52·2 -10 :8 +245 :50 |
31. Обчислити усно:
|
а) |
2,5-1,6; 3,2-1,4; 0,47-0,27; 0,64-0,15; 0,71-0,28; |
б) |
1,8+2,5; 2,7+1,6; 0,63+0,17; 0,38+0,29; 0,55+0,45; |
в) |
3,4-0,2; 2,6-0,05; 4,52-1,2; 4-0,8; 1-0,45; |
г) |
5+0,35; 3,7+0,24; 0,46+1,8; 0,57+3; 1,64+0,36; |
32.
|
|
Клоун, щоб посмішити публіку, розказав одну історію про те, як він ходив на рибалку. В цій історії він навмисно переплутав усі одиниці вимірювання. «Я прокинувся у 4 кг ранку. Поснідав, випив 1 км молока. Потім пішов на ставок. Відстань до нього чимала, 5 °. Вранці було прохолодно, температура всього 10 год тепла. тому я пішов швидко, зі швидкістю 6л. Прийшов, закинув вудку. Не пройшло і 20 см, як я спіймав першу рибину. Величезну, довжиною – 50 хвилин та вагою 3 км/год. Смачна була вуха.» Знайти всі помилки в розповіді. розставити правильно одиниці вимірювання. |
33.Знайдіть правильні рівності:
|
0,2:6=1: |
|
|
|
|
|
2: |
|
|
|
|
|
1,5:3=3:4 |
|
|
|
6,3:3=2:100 |
|
|
|
|
|
|
34.Знайдіть правильні рівності та дізнайтеся прізвище видатного вченого:
|
І |
|
|
А |
|
|
Е |
|
|
Ф |
|
Л |
|
О |
|
||
|
П |
|
Г |
|
С |
1,5:0,18=5:0,6 |
35.Обчисли та розташуй відповіді прикладів у порядку спадання, спів став їх відповідним буквам. Якщо обчислення виконано вірно, то отримане слово – назва другого по висоті діючого вулкана в світі:
|
Л |
(-3)+(+11) |
|
Ю |
(+1,2)+(-0,8) |
|
Ь |
(-0,1)+(-0,02) |
|
О |
(-9)+(-6) |
Л |
(+0,7)+(-2) |
Я |
( |
||
|
Ь |
(+8)+(-10) |
Й |
(-0,4)+(-0,6) |
Я |
(-2,08)+0 |
||
|
К |
(-5)+(-7) |
Ь |
(-0,2)+(+5) |
Л |
( |
36.Обчисли:
|
а) |
-8+5; |
|
д) |
-1,9+2; |
|
и) |
|
|
н) |
2,45-3,7; |
|
б) |
4-6; |
|
е) |
6,4-8; |
|
к) |
0-4,8; |
|
о) |
-6,42-0,358; |
|
в) |
-2-9; |
|
ж) |
-0,5-0,7; |
|
л) |
-1,8+ |
|
п) |
|
|
г) |
-3+7; |
|
з) |
-1,3+0,6; |
|
м) |
-5,2+0; |
|
р) |
-0,64-9,36. |

37.Обчисли та розташуй відповіді прикладів у порядку зростання, спів став їх відповідним буквам. Що означає отримане слово?
|
Т |
(-7)+(-9) |
|
Т |
(-1,4)+(+0,8) |
|
Н |
(+0,05)+(-0,5) |
|
К |
(-3)+(+12) |
У |
(-0,9)+(-0,5) |
И |
( |
||
|
И |
(+5)+(-11) |
Р |
(-3,7)+(-4) |
К |
(-3,6)+0 |
||
|
И |
(-4)+(-8) |
Р |
(-2,9)+(+6) |
Ж |
( |
38.Обчисли:
|
а) |
-3+9; |
|
г) |
4,5-5; |
|
ж) |
0,75- |
|
к) |
1,08-2; |
|
б) |
5-7; |
д) |
-0,6-0,8; |
з) |
0-2,4; |
л) |
-2,56-4,4; |
|||
|
в) |
-4-6; |
е) |
-2,9+5,4; |
и) |
-2,6+ |
м) |
|
39. Обчисли усно:
|
а) |
0,14+0,06; |
б) |
3,18-1,08; |
в) |
5,7+0,13; |
г) |
0,42; |
|
2-0,7; |
2,06+1,04; |
2,85-1,5; |
0,32; |
||||
|
100·0,012; |
5,4·0,1; |
0,8·0,5; |
0,052; |
||||
|
0,42:7; |
4,08:4; |
0,5:2; |
0,013. |
40. Актор, виступаючи перед учнями, розповів їм про те, як їздив збирати гриби. Він переплутав деякі одиниці вимірювання величин і просив школярів виправити його. Розповідь була такою: « Прокинувся я і подивився на годинник. Стрілки показували 6 м. ранку. Швиденько поснідав і зі своїм другом поїхав до найближчого лісу, віддаленого від нашого міста на 20кг . Ранок був холодний, t не перевищувала 7 л тепла. Щоб зігрітись ми швидко йшли лісом в середньому по 5º за годину. зайшовши у ліс на відстань біля 2ц , ми потрапили на поляну, де росло 25 білих грибів. Найбільший з них мав масу понад 400год. На відстані 200 га трапилася нова поляна з якої ми теж зібрали не менш 2 вольт грибів. Прекрасний був настрій і ми гарно відпочили того дня. Через 4 милі ми повернулися до свого автомобіля і задоволені поїхали до дому.
Вкажи усі помилки у розповіді.

41. Клоун показав чотири буквені вирази : а) х+1 б) 100 – х в)2х – 1 г) 4 : х.
Він сказав що жодне з них не приймає значення 1 ні при якому значенні букви х.
Чи помилявся клоун? Виправте його, знайдіть значення х, при яких вирази дорівнюють
42. Відновити ланцюжок обчислень:
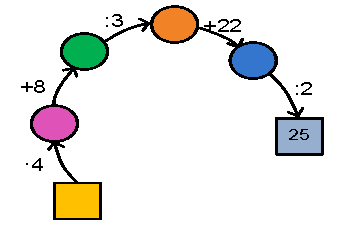
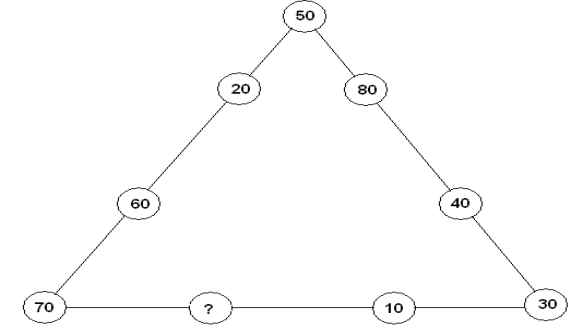
43. У кружальцях розмістити числа 1,2,3,4,5,6,7,8,9 так, щоб їх сума вздовж кожного з відрізків АВ, ВС, СА дорівнювала 20.
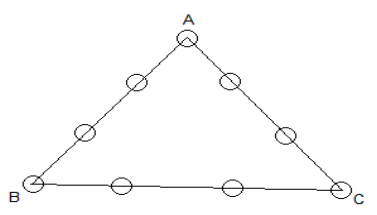
44. Назвіть формулу периметру квадрата. Обчислити при а = 3см.
Периметр прямокутника. Обчислити при а = 7см, b = 5см.
Шлях, пройдений автомобілем, що рухається зі швидкістю 63 км/год, за
- год.
45. Розв’яжіть рівняння:
а) 2 ·х + 1 = 7 б) 2 · х – 3 = 11 в) 17 – 3 · х = 8 г) 8+ 3 · х = 20
д) у : 4 = 6604 : 4
46. При яких значеннях m вірна рівність:
 4·( m – 5) = 4m – 20 ?
4·( m – 5) = 4m – 20 ?
47. Обчислити усно:
|
а) |
6:1,2 -5 ·0,97 +3,15 |
в)
г) |
3·16 -1,2 :12 +1,2 |
д) |
30·0,3 -4,8 :0,7 ·0,01 |
ж) |
7-0,7 :0,9 ·0,02 +0,66 |
||||
|
? |
? |
? |
? |
||||||||
|
|
|||||||||||
|
б) |
9:1,5 -5 ·0,25 +6 |
|
0,6·6 +1,2 :40 ·50 |
е) |
2·1,9 -2,2 :0,8 :0,1 |
з) |
1,5·6 :5 ·2 +2,4 |
||||
|
? |
? |
? |
? |
||||||||
48. Розкрий дужки:
6 · ( 10+с) 12·( х - у) ( 16+у)·4 5·( х+13+у)
7 · ( d - 8) (а+2+в)·24 ( 13 –х)·5 7·(к – 15+у)
(а+в) · 6 (u –v+3)·21
49. При якому а вірна рівність?
а · 2 = 2 а · а = а
а · 2 = 0 а · 2 - 3 = 7
а · 1 = 1 (а - 3) · 2 = 13
а · 1 = а
50. Виконайте дії за схемою:
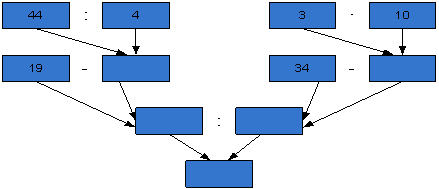
51.Знайдіть значення виразів:

317 · 1+ 233 : 1 7218 : 7218 + 999 · 1
(657 – 656) · 49 – 36 634 : (1000 – 999) + 66
4506 · 0 + 6473 : 1 3208 : 3208 · 5628 : 5628
52.
|
.
|
|
Клоун сказав глядачам: « У мене є 6 карточок з числовими виразами. Я зараз сполучу їх знаками рівності і покажу вам одну властивість додавання». В цей момент погасло світло й клоун вільно розклав картки. От що одержав клоун: |
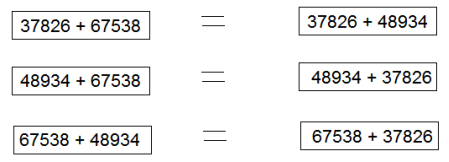
Глядачі сміялися. Усі бачили, що рівності невірні. Не обчислюючи сум, вкажіть двійки карточок, на яких записані рівні між собою суми. Яку властивість бажав показати клоун?
53.Знайдіть значення виразу:
7a + 7b, якщо a + b = 23;
x · 13 + y · 13, якщо х + у = 10;
8c – 8d, якщо c – d =12
m · 21 – n · 21, якщо m – n = 3.
54.
|
|
|
Клоун почав підраховувати у стовпчик суму таких чисел: |
|
|
999 + 999 999 999 5 ---------- |
Він довго плутався, зопрів, але ніяк не міг підрахувати суму. Глядачі сміялися. Усі бачили, що таку суму легко підрахувати в умі, якщо здогадатися, що кожний доданок 999 треба доповнити до …?
Назвіть результат.
|
||
55. Знайдіть закономірність і продовжить ряд чисел:
а) 2, 5, 8, 11, 14,… в) 3, 33, 333, 3333,…
б) 1, 5, 9, 13, 17,… г) 3, 30, 300, 3000,…

56. Обчисли усно:
|
|
|
1- |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57. Назвіть усі відрізки, зображені на малюнку:
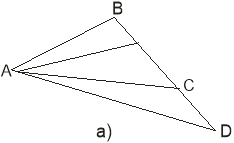
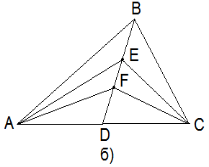
58. Виконайте дії:
|
|
|
|
|
-0,42:0,4 |
|
(-0,4)2 |
|
3,4-45 |
-0,4·(-0,25) |
36,18:(-1,8) |
-0,42 |
|||
|
|
|
-1,53:(-1,5) |
(-0,2)3 |
59.Довжина прямокутника 22 см, а його ширина складає 4/11 від довжини. Який периметр прямокутника?
60.Периметр трикутника 63 м. Одна з його сторін складає 2/9 від периметру, а друга - 3/7. Знайти сторони трикутника.
61.Площа прямокутника 20 дм2, його ширина 4 дм. Скільки відсотків становить довжина прямокутника від його ширини?
62.Довжина відрізка КL дорівнює 12м, а довжина відрізка МN дорівнює 60 м.
а) Знайти відношення довжини КL до довжини МN. Що показує це відношення?
б) Знайти відношення довжини МN до довжини КL. Що показує це відношення?
63.
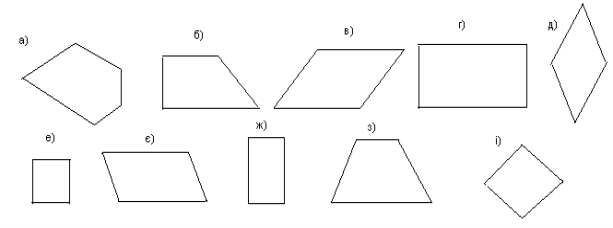
Розгляньте малюнок і назвіть, яка з фігур є:
а) прямокутником б) паралелограмом в) квадратом
64. Чому дорівнює довжина і площа круга, діаметр якого дорівнює 2 см
65. Розв’язати приклади:
|
|
|
20:(0,4) |
|
|
|
-5,4:0,06 |
-0,15:1,5 |
9,6:(-0,001) |
||
|
|
|
|
||
|
3,2-9 |
-10:(-18) |
-50·(-0,16) |
||
|
|
|
|
|
|

Світлана Василівна
Пазиненко
Усний рахунок для кмітливих
в 5-6 класах
Методичний посібник
 Для нотатків
Для нотатків
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
-
Дякую за матеріал і за роботу
-


про публікацію авторської розробки
Додати розробку


