Позакласна робота "Приклади завдань на відсоткові розрахунки"

Особливу увагу вчителі математики мають приділяти залученню здобувачів освіти до позакласної роботи з предмету. Наведу приклади завдань на відсоткові розрахунки, які можна використати під час проведення  математичних конкурсів, шкільної олімпіади з математики тощо.

Задача 1. Об'єм води, що перетворюється на лід, збільшується на 9%. На скільки відсотків зменшиться об'єм, якщо лід розтане? (Вкажіть найточніший результат)

Розв'язання. Нехай х – об'єм води, 1,09х – об'єм льоду. Після танення втрачається 0,09х цього об'єму, що становить

100%8,25%.

Отже, після танення льоду об'єм зменшиться на 8,25%.

Задача 2. 4 кг розчину з 25-відсотковим вмістом розчиненої у воді солі змішали з 4 кг 40-відсоткового розчину солі і ще додали 2 кг чистої води. Вкажіть відсотковий вміст солі в отриманому розчині.

Розв'язання. Знайдемо масу солі в 4 кг першого розчину:

4 0,25 = 1 (кг).

Знайдемо масу солі в 4 кг другого розчину:

4 0,4 = 1,6 (кг).

В обох розчинах 1 + 1,6 = 2,6 (кг) солі. Додали 2 кг чистої води, тому відсотковий вміст солі в отриманому розчині (10 кг) становить

2,6 : 10 100% = 26%.

Задача 3. Із 12200 родин міста 70% мають дачу, 74% мають автомобіль,  86% – рахунок у банку. Скільки родин з цієї кількості обов'язково мають і дачу, і автомобіль, і рахунок у банку?

Розв'язання. З умови задачі випливає, що 30% родин міста не мають дачі, 26% родин не мають автомобіля, 14% – рахунку в банку. Отже, не більше 70% родин не мають або дачі, або автомобіля, або рахунку в банку (може бути поєднання двох з цих предметів або всіх трьох). Тому не менше 30% родин мають і дачу, і автомобіль, і рахунок у банку:

12200 0,3 = 3660 (родин)

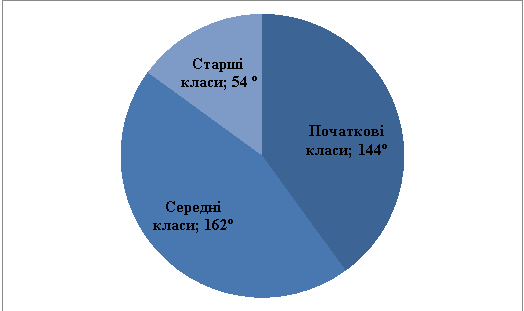Задача 4. На круговій діаграмі показано розподіл учнів деякої школи по трьох групах: початкові класи (1-4) – 144, середні класи (5-9) – 162, і старші класи (10-11) – 54.

1) Укажіть, скільки відсотків учнів школи становить кожна з груп.

2) Відомо, що кількість учнів 10-11 класів на 120 менша від кількості учнів середніх класів. Знайдіть кількість учнів  школи.

3) Складіть таблицю розподілу учнів по класах від першого до одинадцятого, врахувавши, що у класах відповідної групи навчається приблизно однакова кількість учнів.

 Розв'язання. 1) Круг має 360 тому учні початкових класів становлять

144360 100% = 40%,

учні середніх класів –

162 : 360 100% = 45%,

старших класів –

54 : 360 100% = 15%

від усієї кількості учнів школи.

2) Різниця кількості  учнів середніх класів і старших класів становить 120 або 30%, тому у закладі освіти навчається

120 : 30%100% = 400 (учнів)

3) У початкових класах навчається

400 = 160 (учнів),

у середніх класах –

400 0,45 = 180 (учнів),

у старших –

400 0,15 = 60 (учнів).

Тому у 1-4 класах є приблизно по 40 учнів (160 : 4 = 40), у 5-9 класах – по 45 учнів (180 : 5 = 45), у 10-11 класах – по 30 учнів (60 : 2 = 30).

Задача 5. Приватне підприємство, яке реалізує печиво, проводить рекламну акцію з метою збільшення обсягу продажу. У кожну коробку вкладається акційна картка. За 10 накопичених карток покупцеві видають безкоштовно коробку печива. На скільки відсотків приватне підприємство повинно підвищити вартість коробки печива, якщо на рекламу додаткові кошти не виділяються.

Розв'язання. Оскільки до вартості кожної з десяти коробок печива додається десята частина вартості одинадцятої коробки, то вартість коробки печива збільшується на  від попередньої вартості, тобто на 10%.

Такі задачі розвивають у школярів інтерес до предмету, допомагають у виборі майбутньої професії. Якщо учасник математичного турніру чи шкільної олімпіади й не став переможцем чи призером, він переміг, насамперед, себе, свою інертність і байдужість, та отримав досвід, набув нових знань.