Позакласний захід до математичного тижня. Слідство ведуть колобки: "Математичні софізми і парадокси"
По-перше, розбір софізмів, насамперед, розвиває навички логічного мислення, тобто прищеплює навички правильного мислення.
Зрозуміло! Якщо дитина доторкнеться до гарячого предмету, вона намагатиметься більш цього не робити. Так і учень, який усвідомив помилку, буде проявляти обережність у математичних міркуваннях.
Ну, а по-друге? По–друге, що особливо важливо, розбір софізмів допомагає свідомому засвоєнню математики, розвиває спостережливість, критичне відношення до того, що вивчається. І, нарешті, це просто цікаво!
Слідство ведуть колобки
Як стати мільйонером(2 грн)2 = (200 коп)2 Піднесення до квадрату величин не має змісту2 грн. = 200 коп. Піднесемо ліву та праву частину рівності до квадрату:4 грн = 40000 коп. Отримаємо Де помилка?= 400грн.
Так як 1:1=1, то 2∙2=5 Помилка зроблена при винесенні спільних множників 4 з лівої частини і 5 з правої. Насправді, 4:4=1:1, але 4:4≠4(1:1). Напишемо вираз 4:4=5:5. Винесемо з кожної частини рівності спільний множник за дужки, отримаємо:4(1:1)=5(1:1) або(2·2)(1:1)=5(1:1)Де помилка?2·2=5
або2a = 2b, і остаточно a = b, т.б. ВСІ числа рівні між собою. Вилучаючи з обох частин рівності (a - b)2 = (b - a)2 квадратні корені, насправді отримаємо |a – b | = |b - a|, а розкриваючи знак модуля отримаємо: a - b = a – b. Візьмемо два довільних нерівних між собою числа a і b і запишемо для них очевидну тотожність:a2 - 2ab + b2 = b2 - 2ab + a2зліва та справа стоять повні квадрати, т.б. можемо записати(a - b)2 = (b - a)2 Вилучаючи з обох частин останньої рівності квадратні корені, отримаємо:a - b = b - a. Де помилка?всі числа рівні між собою.
вага слона дорівнює вазі комаря
І остаточно х=у, т.б. вага слона дорівнювати вазі комара. Нехай х – вага слона, у – вага комара. Позначимо їх суму через 2а:х+у=2а. З цієї рівності можна дістати ще дві:х-2а=-у та х=-у+2а. Перемножимо почленно останні дві рівності:(х-2а)х=-у(-у+2а)х2-2ах=у2-2ау. Додамо до останньої рівності а2 , отримаємох2-2ах+ а2=у2-2ау+ а2або(х - а)2 = (у - a)2а значить, х-а=у-а
Помилка у міркуваннях аналогічна до помилки у попередньому прикладі, коли беручи квадратний корінь з виразів, повинні отримати модулі цих виразів. Де помилка?
Три друга вирішили зупинитися на ніч в готелі і скинулися по 10 доларів на номер. Один з них пішов платити і з'ясував, що номер коштує 25 доларів. Не знаючи, як розподілити решту 5 доларів, він вирішив повернути кожному по долару, а два залишити собі. Питання з самого початку задано невірно! Долар нікуди не подівся, рахувати просто треба вміти.30-3=27 і при чому тут ще плюс 2, якщо пацан 2 узяв з цих 27?Задача про зо доларів. Де помилка?Виходить, кожен з них заплатив по 9 доларів і ще залишилося 2, в сумі 9x3 + 2 = 27 + 2 = 29. Куди зник ще один долар?
64=65 або 8∙8=65𝑆=8∙8=64кв.од. S=12∙10∙13=65кв.од. 𝑆=5∙13=65кв.од.
У Стародавній Греції були філософи, які займалися навчанням учнів складанню софізмів. СОФІЗМ – це хибне міркування, яке видається за правильне. СОФІЗМ – грецького оходження (sophisma) і означає видумка, хитрість.
Безмежні сходинки
«Краса – велика сила»«Краса потребує жертв»«Краса врятує світ» Парадокс про красуЄ три твердження: Як велика сила, що потребує жертв, може врятувати світ?
Накреслимо на прямокутному аркуші 10 вертикальних ліній однакової довжини. Проведемо діагональ. Розріжемо прямокутник по діагоналі і зсунемо нижню частину вниз, як показано на малюнку. Порахуємо кількість вертикальних ліній.Їх стало 9! Парадокс з лініями
”Математичні софізми і парадокси”
Мета заходу: формування критичного мислення, вміння уважно слухати та розуміти розв’язання математичних задач, чітко та аргументовано
висловлювати свої думки, розвивати спостережливість, навички логічного мислення
Вчитель.
Доброго дня! Я і учні 11 класу раді вітати вас на нашому незвичайному заході, бо сьогодні у вас є унікальна можливість взнати, Як стати мільйонером... або зробити з мухи слона ... І довідатися, що двічі по два не завжди чотири.
Для цього нам треба провести розслідування. За нашим розслідуванням, щоб ми все зробили правильно, невидимо для нас будуть спостерігати брати детективи - колобки. (1 слайд)
Учень1.
Я знаю спосіб швидко збільшити свій капітал та стати мільйонером.
2 грн. = 200 коп.
Піднесемо ліву та праву частину рівності до квадрату:
(2 грн)2 = (200 коп)2
Отримаємо
4 грн = 40000 коп. =400грн.
Де помилка?
Піднесення до квадрату величин не має змісту
Учень2.
А я можу довести, що 2· 2=5
Напишемо вираз
4:4=5:5.
Винесемо з кожної частини рівності спільний множник за дужки, отримаємо:
4(1:1)=5(1:1)
або
(2· 2)(1:1)=5(1:1)
Так як 1:1=1, то 2· 2=5
Де помилка?
Помилка зроблена при винесенні спільних множників 4 з лівої частини і 5 з правої. Насправді, 4:4=1:1, але 4:4≠4(1:1).
Учень3.
А чи знаєте ви, що всі числа рівні між собою. Хочете доведу?
Візьмемо два довільних нерівних між собою числа a і b і запишемо для них очевидну тотожність:
a2 - 2ab + b2 = b2 - 2ab + a2
зліва та справа стоять повні квадрати, т.б. можемо записати
(a - b)2 = (b - a)2
Вилучаючи з обох частин останньої рівності квадратні корені, отримаємо:
a - b = b - a
або
2a = 2b, і остаточно a = b, т.б. всі числа рівні між собою.
Де помилка?
Вилучаючи з обох частин рівності (a - b)2 = (b - a)2 квадратні корені, насправді отримаємо |a – b | = |b - a|, а розкриваючи знак модуля отримаємо: a - b = a – b.
Учень4.
Чи може вага вага слона дорівнювати вазі комара?
Давайте розберемо це питання.
Нехай х – вага слона, у – вага комара. Позначимо їх суму через 2а:
х+у=2а
З цієї рівності можна дістати ще дві:
х-2а=-у та х=-у+2а
Перемножимо почленно останні дві рівності:
(х-2а)х=-у(-у+2а)
х2-2ах=у2-2ау
Додамо до останньої рівності а2 , отримаємо
х2-2ах+ а2=у2-2ау+ а2
або
(х - а)2 = (у - a)2
а значить, х-а=у-а
І остаточно х=у, т.б. вага слона дорівнювати вазі комара.
Де помилка?
Помилка у міркуваннях аналогічна до помилки у попередньому прикладі, коли беручи квадратний корінь з виразів, отримаємо модулі цих виразів.
Учень5.
Класична задача про гроші.
Задача про 30 доларів: Три друга вирішили зупинитися на ніч в готелі і скинулися по 10 доларів на номер. Один з них пішов платити і з'ясував, що номер коштує 25 доларів. Не знаючи, як розподілити решту 5 доларів, він вирішив повернути кожному по долару, а два залишити собі. Виходить, кожен з них заплатив по 9 доларів і ще залишилося 2, в сумі 9x3 + 2 = 27 + 2 = 29. Куди зник ще один долар?
Де помилка?
Питання з самого початку задано невірно! Долар нікуди не подівся, рахувати просто треба вміти.
30-3=27 і при чому тут ще плюс 2, якщо пацан 2 узяв з цих 27?
Учень 6.
Розглянемо квадрат зі стороною 8 одиниць. Його площа відповідно дорівнює 64 кв.од.
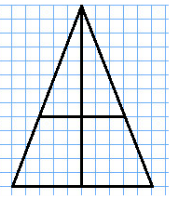Розріжемо його, як показано на малюнку і складемо з цих частин нову фігуру – трикутник.
Не важко побачити, що площа цього трикутника дорівнює
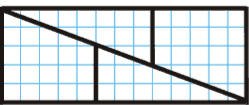10∙13:2=65 кв.од.
Або складемо прямокутник. І знову бачимо, що його площа дорівнює 5∙13=65 кв.од.
Можемо зробити такі висновки: або 64=65, або 8∙8=65.
В чому помилка?
Втрати і прирости площі пояснюються невеликими перекриттями або просвітами уздовж розрізів.
Вчитель.
Ви дуже цікаво розповідаєте, але все ж таки всі міркування, викладені вами, в математиці називаються одним словом – софізм.
СОФІЗМ (від грецького sophistes – той хто вміє мудрувати, дотепно вигадувати) – логічно недостатній умовивід, в якому хибні посилки видаються за істинні або робиться висновок з порушенням законів логики.
Софізм заснований на навмисному, свідомому порушення правил логіки. Яким би не був софізм, він завжди містить одну або кілька замаскованих помилок. Математичний софізм – дивовижне твердження, доведення якого криються непомітні, а часом і досить тонкі помилки.
Софізми з'явилися ще в Стародавній Греції. Вони тісно пов'язані з філософської діяльністю софістів — платних учителів мудрості, що учили всіх бажаючих філософії, логіки і, особливо, риторики (науці і мистецтву красномовства).
Одне з основних завдань софістів полягало у тому, щоб навчити людину доводити (підтверджувати або спростовувати) все, що завгодно, виходити переможцем з будь-якого інтелектуального змагання. Для цього вони розробляли різноманітні логічні, риторичні і психологічні прийоми.
До логічних прийомів нечесного, але вдалого ведення дискусії і відносяться софізми.
Але крім софізмів у математиці і не тільки, використовують і парадокси.
ПАРАДОКС (грецьке paradoxos – дивний, несподіваний) – несподівані явища або висловлювання, які формою або змістом суперечать нашим знанням і уявленням. У парадоксах можуть висловлюватись істинні думки, які дуже розходяться з нашими уявленнями або форма висловлювання яких несподівана. Здебільшого в парадоксах висловлюють неправильні твердження в зовнішньо переконливій формі.
Наприклад:
Безмежні сходинки. Вони представляють головний мотив цієї картини. Прямокутник внутрішнього дворика замкнутий стінами будівлі, у якої замість даху - нескінченні сходинки.
Або парадокс «Про красу».
Є три твердження:
«Краса – велика сила»
«Краса потребує жертв»
«Краса врятує світ»
Як велика сила, що потребує жертв, може врятувати світ?
Парадокс!
Спробуємо практично розібрати ще один математичний парадокс.
Парадокс з лініями
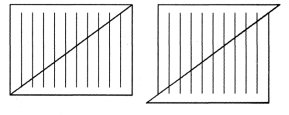Накреслимо на прямокутному аркуші 10 вертикальних ліній однакової довжини. Проведемо діагональ. Розріжемо прямокутник по діагоналі і зсунемо нижню частину вниз, як показано на малюнку. Порахуємо кількість вертикальних ліній.
Їх стало 9!
А зараз ви самостійно зробите парадокс. «Об’ємна рука».
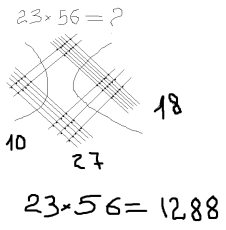
І на самий останок. Проведемо ще один експеримент. «Множення двозначних і тризначних чисел методом прямих».
Підсумок.
А чим корисні софізми для тих, хто вивчає математику?
По-перше, розбір софізмів, насамперед, розвиває навички логічного мислення, тобто прищеплює навички правильного мислення.
Зрозуміло! Якщо дитина доторкнеться до гарячого предмету, вона намагатиметься більш цього не робити. Так і учень, який усвідомив помилку, буде проявляти обережність у математичних міркуваннях.
Ну, а по-друге? По–друге, що особливо важливо, розбір софізмів допомагає свідомому засвоєнню математики, розвиває спостережливість, критичне відношення до того, що вивчається. І, нарешті, це просто цікаво!
1
про публікацію авторської розробки
Додати розробку