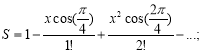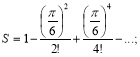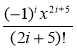Практична робота "Побудова ітераційних циклічних алгоритмічних процесів"

Практична робота №3

ПОБУДОВА ІТЕРАЦІЙНИХ ЦИКЛІЧНИХ АЛГОРИТМІЧНИХ ПРОЦЕСІВ

Мета: Навчитись складати алгоритми ітераційних циклічних алгоритмічних процесів,  будувати блок-схеми циклів з параметром, передумовою та післяумовою.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Багато задач у математиці передбачає використання числових методів, в яких обчислення проводиться до досягнення заданої точності. Так, наприклад, обчислення суми нескінченого ряду Тейлора проводиться до тих пір, поки наступний член ряду за абсолютним значенням стане меншим за значення точності , де  – достатньо мале число. При розв’язуванні таких задач наперед не відома кількість ітерацій циклу. 

Ітераційним циклом називається цикл, число повторень дій в якому невідомо і не може бути обчислено до виконання циклу.

При реалізації ітераційних обчислювальних процесів в алгоритмах повинне забезпечуватися обов'язкове виконання умови виходу з циклу, збіжність ітераційного процесу.

ПОБУДОВА АЛГОРИТМІВ ІТЕРАЦІЙНИХ ЦИКЛІЧНИХ ОБЧИСЛЮВАЛЬНИХ ПРОЦЕСІВ

Задача 1

Скласти блок-схему алгоритму обчислення значення суми нескінченного ряду з заданою точністю ε та кількість елементів в частковій сумі цього наближення.

Розв’язок

Рис. 1. Блок-схема алгоритму 1

Приклад 2

Скласти блок-схему алгоритму знаходження суми членів ряду з точністю  для елемента ряду. Формула загального члена ряду має такий вигляд:

Тобто, обчислити суму ряду з точністю ε:

Розв’язок

Математичне формулювання задачі

Для обчислення суми ряду слід реалізувати цикл, в якому обчислюється значення чергового доданку та накопичується сума за ітераційною формулою

S_i=S_i-1+a_i

В зв’язку з наявністю факторіалу для обчислення а_і доцільно використовувати не пряме обчислення за загальною формулою, а рекурентне співвідношення

a_i=a_i-1k          

Блок-схема алгоритму зображена на рис. 2.

Рис. 2. Блок-схема алгоритму 2

Приклад 3

Скласти блок-схему алгоритму знаходження найменшого номера n члена послідовності n=1,2,3…,для якого різниця між знайденим та попереднім членами послідовності за модулем не перевищує заданої точності, тобто виконується умова . Вивести на екран всі елементи послідовності до n-го включно.

Розв’язок

Для даної задачі блок-схема алгоритму буде мати вигляд, зображений на рис. 3.

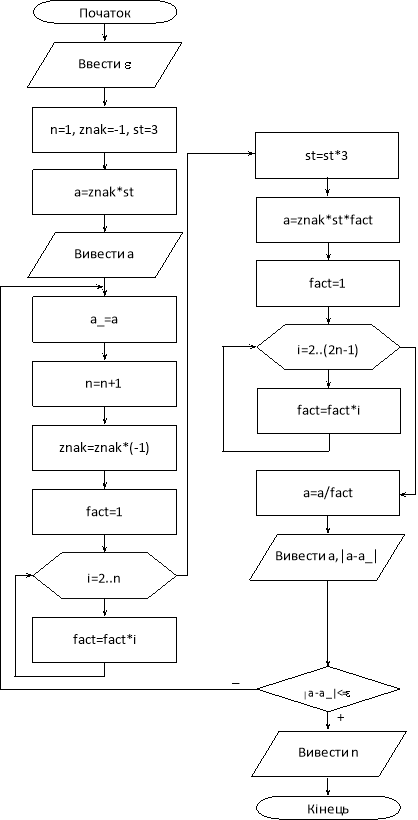
Рис. 3. Блок-схема алгоритму 3

Для знаходження номера члена ряду, для якого виконується зазначена умова, використаємо цикл з післяумовою, в середині якого потрібно по черзі записати два рази цикл з лічильником:  перший – для знаходження факторіала числа n, другий – для знаходження факторіала числа 2n - 1 відповідно до формули загального члена ряду.

Завдання

Завдання 1

Скласти блок-схему алгоритму обчислення значення суми нескінченного ряду (див. таб.1) з заданою точністю ε та кількість елементів в частковій сумі цього наближення.

Таблиця 1. Варіанти завдань

Завдання 2

Скласти блок-схему алгоритму знаходження найменшого номера i (i=1,2,3…) члена послідовності (див. таб.2), для якого різниця між знайденим та попереднім членами послідовності за модулем не перевищує заданої точності, тобто виконується умова . Вивести на екран всі елементи послідовності до i-го включно.

Формула загального члена ряду має вигляд, представлений в таблиці 2.

Таблиця 2. Варіанти завдань

Висновки

1. Ітераційним циклом називається цикл, число повторень дій в якому невідомо і не може бути обчислено до виконання циклу.
2. Для організація ітераційного циклічного процесу використовуються структури повторення з передумовою або післяумовою, оскільки наперед невідома кількість повторень.
3. Дуже часто в ітераційних циклах обчислюються певні значення з заданою точністю.

ВИМОГИ ДО ЗВІТУ

У звіті з практичної роботи повинні бути відображені:

1. Тема, мета практичної роботи.
2. Короткі теоретичні відомості з теми.
3. Завдання практичної роботи.
4. Блок-схеми алгоритмів розв’язку задач.
5. Висновок.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Що таке цикл і як він працює?
2. Який цикл ми називаємо ітераційним?
3. Що таке цикл з передумовою і післяумовою? Чим вони відрізняються?
4. Яка необхідна дія повинна бути записана в тілі циклу з передумовою і тілі циклу з післяумовою?
5. Що таке нескінченний цикл? Коли трапляються такі випадки?