Практична робота 4:"Табличний процесор Excel"

ПРАКТИЧНА РОБОТА № 4.

 

 

 Тема: Побудова графіків функцій. Розв'язання нелінійних рівнянь. Використання майстра діаграм.

Ціль: Навчитися будувати графік функції та розв’язувати нелінійні рівняння в MS Excel.

 

 

МЕТОДИЧНІ ВКАЗІВКИ.

 

1.        Побудова прогресії за допомогою майстра діаграм

 

Для побудови графіків в MS Excel є майстер діаграм, що пропонує користувачу великий набір типів графіків і діаграм, що дозволяють наочно представити отримані дані. Розглянемо технологію    побудови    графіка    на    прикладі    функції  при х [0; 1]. Процес побудови графіка функції складається зі створення таблиці значень функції і безпосередньої побудови графіка. Для побудови графіка функції  необхідно  спочатку  побудувати таблицю її значень при різних значеннях аргументу, причому аргумент звичайно беруть із фіксованим кроком. Крок вибирають невеликим, у нашому випадку візьмемо 0,1.

Нам треба знайти y(0), y(0,1), y(0,2),… y(1). Із цією метою в комірки діапазону А1:А11 послідовно введемо 0,  0,1, …, 1, тобто значення змінної х. Ця послідовність значень являє собою арифметичну прогресію. Ввести в комірки діапазону ряд послідовних значень, що утворять арифметичну прогресію, можна двома способами (при введенні в комірку десяткових дробів варто використовувати кому ( , ) як роздільник цілої й дробової частини, однак у даних методичних вказівках як роздільник вказується крапка ( . ), тому треба при необхідності здійснювати заміну):

 

1.  В комірки А1 й А2 введіть перший і другий члени арифметичної прогресії.

2.   Виділіть діапазон комірок A1:A2.

3. Розташуйте вказівник миші на маркері заповнення виділеного діапазону та простягніть його вниз (на діапазон A3:A11) доти, поки не утвориться числовий ряд потрібної довжини.

 

Або:

 

1.  Введіть перший член арифметичної прогресії в комірку A1.

2.  Виберіть меню Правка-> Заполнить-> Прогрессия.

3. У діалоговому вікні Прогрессия в групі Расположение виберіть перемикач по столбцам, а в групі Тип - перемикач Арифметическая. У поле Шаг введіть значення 0,1,  а в поле Предельное значение - 1.

4.  Натисніть кнопку ОК.

 

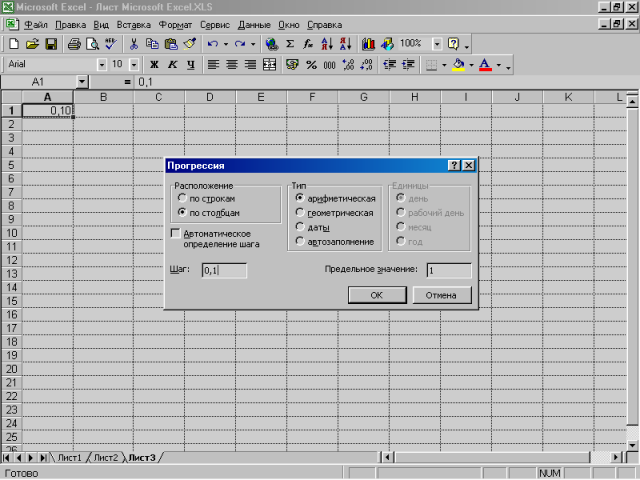
Мал. 4.1. Завдання кроку та граничного значення прогресії

 

Вікно Прогрессия закриється, а на робочому листі автоматично буде побудована необхідна прогресія.

Введіть в комірку В1 формулу =COS((ПИ)*A1)^2. Автоматично порахується значення функції для першого члена прогресії в комірці А1. Тепер виберіть комірку В1, розташуйте вказівник миші на маркері заповнення виділеної комірки і пробуксуйте його вниз на діапазон В2:В11, на цьому процес створення таблиці значень функції буде завершений.

Значення функції після підрахунку відображаються з різною кількістю десяткових знаків, крім того, відбувається перемішування числового та експонентного форматів (в комірці 5 замість 0 відображається 3.75Е-33, що приблизно дорівнює нулю). Формати варто привести до загального виду, наприклад, щоб значення аргументу виводилися в числовому форматі з точністю до одного знака після десяткової крапки, а значення функції - з точністю до трьох знаків після десяткової крапки. Відформатуємо значення аргументу. Для цього треба вибрати діапазон А1:А11, і вказати команду Формат -> Ячейки. У діалоговому вікні Формат ячеек на вкладці Число в списку Числовые форматы виберіть Числовой, а в поле Число десятичных знаков введіть 1. Натисніть кнопку ОК. Аналогічно відформатуйте діапазон В1:В11.

 

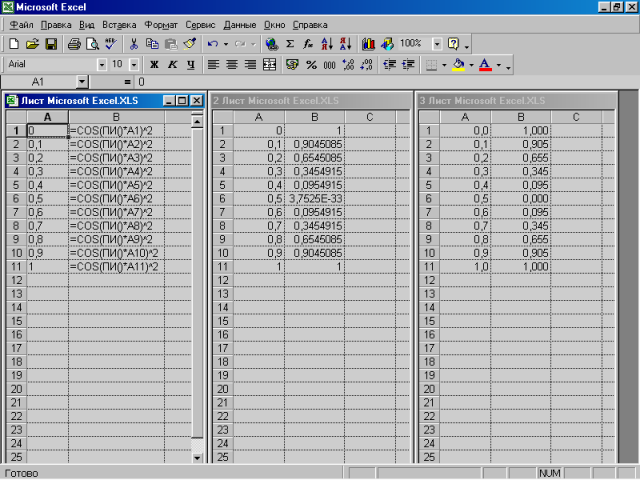
Мал. 4.2. Табуляція функції до і після форматування даних

 

 

4.2. Побудова графіка функції

 

Для побудови графіка функції:

 

1. Виберіть команду Вставка -> Диаграмма.

2. У діалоговому вікні Мастер диаграмм на вкладці Стандартные в списку Тип виберіть варіант График, а в списку Вид вкажіть Стандартный график. Натисніть кнопку Далее.

3. У діалоговому вікні Мастер диаграмм (шаг 2 из 4) : (яке пізніше перейменовується у вікно Исходные данные) на вкладці Диапазон данных виберіть перемикач Ряды в столбцах, тому що дані розташовуються у стовпцях. У поле введення Диапазон приведіть посилання на діапазон комірок В1:В11, значення з яких відкладаються уздовж осі ординат. Зверніть увагу на отриманий графік функції, відображуваний на вкладці Диапазон данных. У ньому по осі ординат відкладаються значення функції, а по осі абсцис порядкові номери точок, а не значення аргументу. Для того, щоб по осі абсцис відкладалися значення аргументу, варто скористатися вкладкою Ряд.

4. На вкладці Ряд у поле введення Подписи оси X приведіть посилання на діапазон комірок A1:A11, значення з яких відкладаються по осі абсцис. Посилання на цей діапазон вводьте не із клавіатури, а шляхом  його  вибору  на

 

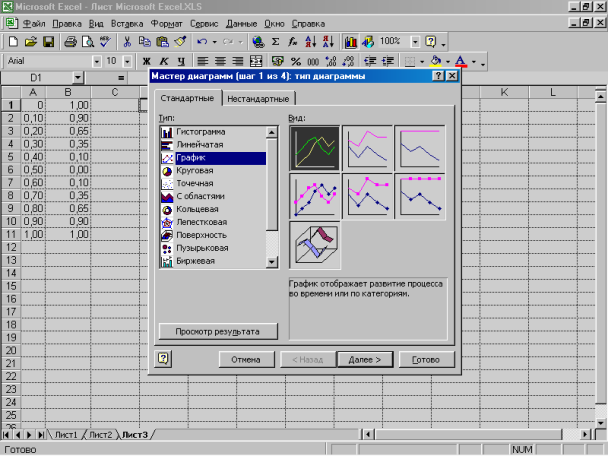
Мал. 4.3. Вікно майстра діаграм

 

 

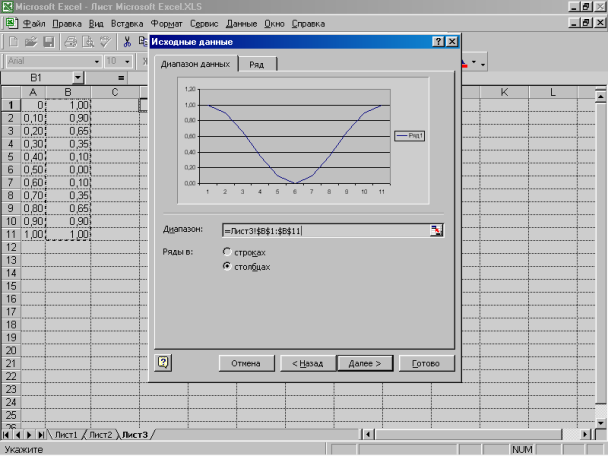
Мал. 4.4. Вкладка вихідних даних (діапазон) у вікні майстра діаграм

робочому листі. Наприклад, виберіть комірку А1, а потім при натиснутому <Shift> виділіть комірку А11.

У результаті в поле Подписи оси X автоматично буде сформоване посилання на цей діапазон. Якщо в цьому полі введення не вказувати посилання ні на який діапазон, то дані, що відкладають по осі ординат, нумеруються в природному порядку, починаючи з 1, а уздовж осі абсцис будуть розміщатися їхні порядкові номери.

У списку Ряд приводяться ряди даних, що відкладають по осі ординат, у нашому випадку є тільки один ряд даних. Ці ряди автоматично визначаються на основі посилання, зазначеного в поле введення Диапазон попереднього кроку алгоритму. У поле Значение автоматично виводиться посилання на діапазон, що відповідає обраному ряду зі списку Ряд. У поле введення Имя відображається посилання на комірку, у якій міститься заголовок відповідного ряду. Цей заголовок надалі використовується майстром діаграм для створення легенди.

 

 

 

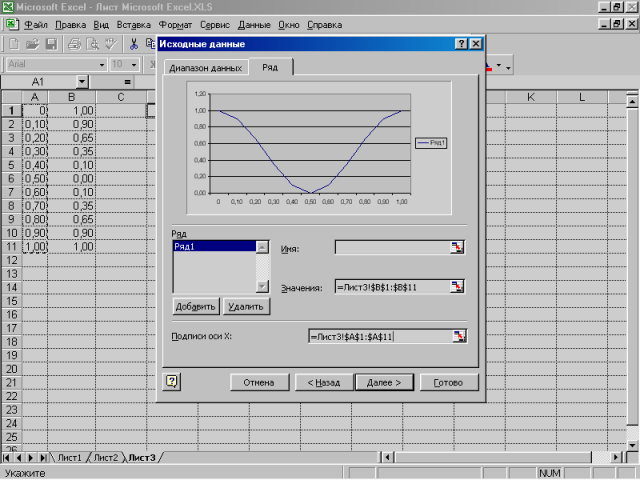
Мал. 4.5. Вкладка вихідних даних (ряд) у вікні майстра діаграм

 

 

Легенда в діаграмі потрібна для того, щоб розрізняти кілька рядів даних, що відкладають по осі ординат. У нашому випадку є тільки один ряд даних, тому легенда нам не буде потрібна. Отже, у поле введення Имя вводити нічого не потрібно. Натисніть кнопку Далее.

5. У діалоговому вікні Мастер диаграмм (шаг 3 из 4) на вкладці Заголовки в поле Название диаграммы введіть Графік, у поле Ось X (категорий) введіть х, у поле Ось Y (значений) введіть y. На вкладці Легенда зніміть прапорець Добавить. Натисніть кнопку Далее.

6.  У діалоговому вікні Мастер диаграмм (шаг 4 из 4) встановіть перемикач Поместить диаграмму на листе в  положення имеющемся. Діаграма буде впроваджена в робочий лист, ім'я якого вказується у відповідному списку. Якщо вибрати перемикач отдельном, то діаграма з'явиться на листі діаграм. Натисніть кнопку Готово.

 

Використовуючи маркери зміни розмірів, можна поміняти розмір діаграми, а також розмістити діаграму в потрібному місці робочого листа. Крім того, припустимі редагування й виправлення зовнішнього вигляду будь-якого елемента діаграми. Для цього досить його виділити, натиснути на праву кнопку миші й з  контекстного меню вибрати команду редагування цього елемента.

 

 

 

 

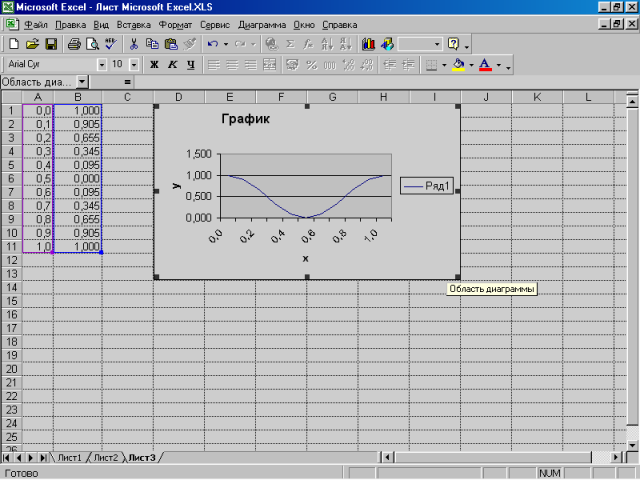
Мал. 4.6. Діаграма (графік), розміщена на поточному листі

 

 

 

 

 

 

4.3. Побудова графіка функції із двома умовами

 

 Розглянемо приклад побудови графіка функції при х  [0; 1]:

 

 

 

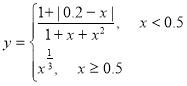
 Графік будується аналогічно графікові функції з однією умовою, за винятком того, що в комірку В1 вводиться формула:

 

=ЕСЛИ(А1<0.5; (1+ABS(0.2-A1)) / (1+A1+A1^2); A1^(1/3))

 

 У формулі ми застосували функцію розгалуження ЕСЛИ(IF), що має такий синтаксис:

 

ЕСЛИ (лог_вираження; значення_якщо_істина; значення_якщо_неправда),

 

лог_вираження - це будь-яке значення або вираження, що приймає значення ІСТИНА (ИСТИНА, TRUE) або НЕПРАВДА (ЛОЖЬ, FALSE).

значення_якщо_істина - це значення, що повертається, якщо лог_вираження дорівнює ІСТИНА. Цей аргумент може бути числом, рядком тексту або формулою.

значення_якщо_неправда - це значення, що повертається, якщо логічне вираження дорівнює НЕПРАВДА. Цей аргумент також може бути числом, рядком тексту або формулою. Якщо лог_вираження дорівнює НЕПРАВДА, а даний аргумент опущений (тобто після  значення_якщо_істина немає крапки з коми), то повертається логічне значення НЕПРАВДА, а якщо аргумент порожній (тобто після значення_якщо_істина стоїть крапка з комою з наступною закриваючою дужкою), то повертається значення НЕПРАВДА.

В MS Excel є також й інші функції логічних умов:

 

1. И(лог_знач1; лог_знач2; ...) / AND(arg1, arg2, ...) - логічне множення. Повертає логічне значення ІСТИНА, якщо всі аргументи мають значення ІСТИНА; повертає значення НЕПРАВДА, якщо хоча б один аргумент має значення НЕПРАВДА.

 

Наприклад: И(2+2=4; 2+3=5) повертає значення ІСТИНА.

 

2. ИЛИ(лог_знач1; лог_знач2; ...) / OR(arg1, arg2, ...) - логічне додавання. Повертає логічне значення ІСТИНА, якщо хоча б один з аргументів має значення ІСТИНА; повертає значення НЕПРАВДА, якщо всі аргументи мають значення НЕПРАВДА.

 

Наприклад: ИЛИ(2+2=4; 2+3=6) повертає значення ІСТИНА.

 

3. НЕ(лог_знач) / NOT(arg) - логічне заперечення. Змінює на протилежне значення логічне значення свого аргументу.

 

Наприклад: НЕ(2+2=5) повертає значення ІСТИНА.

 

 

4.4. Знаходження корінь рівняння

 

Як приклад візьмемо рівняння: x³ – 0,01x² – 0,7044x + 0,139104 = 0

Тому що дане рівняння є поліномом третього ступеня, то для нього є не більше трьох речовинних корíнь. Для знаходження корíнь спочатку потрібно знайти інтервали, на яких ці корені існують. Такими інтервалами локалізації можуть служити проміжки, на кінцях яких функція має протилежний знак. З метою знаходження інтервалів, на кінцях яких функція змінює знак, необхідно побудувати її (тобто протабулювати).  Протабулюємо рівняння на інтервалі      [-1; 1] із кроком 0,2. Для цього:

 

1. Введіть в комірку А2 значення -1, а в комірку А3 - значення       -0,8.
2. Виберіть діапазон А2:А3, розташуєте покажчик миші на маркері заповнення цього діапазону й простягніть його на діапазон А4:А12. Аргумент буде протабульовано.
3. В комірку В2 введіть формулу:

 

=A2^3-0,01*A2^2-0,7044*A2+0,139104

 

4. Виберіть комірку В2. Розташуєте покажчик миші на маркері заповнення цієї комірки та простягніть його на діапазон B3:B12. Функція також протабулюється.

 

З розрахунків видно, що поліном змінює знак на інтервалах [-1; -0,8],  [0,2; 0,4] й [0,6; 0,8], тому на кожному з інтервалів є свій кóрінь; тому що поліном третього ступеня має не більше трьох корíнь, то таким чином вони всі локалізовані.

Перш ніж приступити до знаходження корíнь за допомогою підбора параметра, необхідно виконати підготовчі операції:

- Установіть точність, з якою находиться корінь. Корінь за допомогою підбора параметра находиться методом послідовних наближень. Виберіть команду Сервис -> Параметры й на вкладці Вычисления діалогового вікна Параметры задайте відносну погрішність і граничне число ітерацій рівними 0,00001 й 1000, відповідно.

- Відведіть на листі комірку, наприклад С2, під шуканий корінь. До застосування підбора параметра в ній знаходиться початкове наближення до кореня рівняння, а після застосування - знайдене значення кореня.

- В комірку С2 треба ввести значення, що є наближенням до шуканого кореня. У цьому випадку, першим відрізком локалізації кореня є [-1; -0.8], отже, за початкове наближення до кореня розумно взяти середню точку цього відрізка -0,9.

- Відведіть комірку, наприклад D2, під функцію, для якої ведеться пошук кореня, причому замість невідомої (y) цієї функції повинне вказуватися посилання на комірку, відведену під шуканий корінь. Таким чином, у комірку D2 введіть формулу:

 

=C2^3-0,01*C2^2-0,7044*C2+0,139104

 

Аналогічно робимо із двома іншими шуканими коріннями:

 

- Відвести комірку C3 під другий корінь, ввести в неї початкове наближення 0,3, а в комірку D3 ввести наступну формулу:

 

= C3^3-0,01*C3^2-0,7044*C3+0,139104

 

- Відвести комірку C4 під третій корінь, ввести в неї початкове наближення 0,7, а в комірку D4 ввести наступну формулу:

 

= C4^3-0,01*C4^2-0,7044*C4+0,139104

 

Тепер переходимо  до знаходження першого кореня рівняння:

 

1. Виберіть команду Сервис -> Подбор параметра.

2. У поле Установить в ячейке введіть посилання на комірку D2 (мал. 4.7). У цьому полі дається посилання на комірку, у якій введена формула, що обчислює значення лівої частини рівняння. Для знаходження кореня за допомогою підбора параметра його необхідно представити в такому виді, щоб його права частина не містила змінну (уводити посилання на комірки в поля діалогового вікна Подбор параметра зручніше вибором відповідної комірки на листі, при цьому MS Excel автоматично буде перетворювати їх в абсолютні посилання).

3. У поле Значение введіть 0. Тут вказується значення із правої частини рівняння.

4. У поле Изменяя значение ячейки введіть С2. У даному полі приводиться посилання на комірку, відведену під змінну.

5. Натисніть кнопку ОК.

 

На екрані відобразиться вікно Результат подбора параметра з результатами роботи. Наближене значення кореня поміщене в комірку С2. У цьому випадку воно дорівнює -0,919999. Для наочності одержання нуля в комірці D2 варто встановити в ній числовий формат з 4 десятковими знаками. Аналогічно знаходимо два інші корені, вони рівні 0,21000 й 0,71999.

 

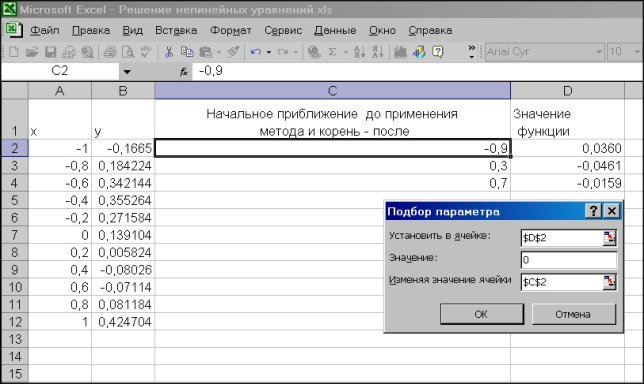
Мал. 4.7. Локалізація корíнь полінома

 

 

 

Мал. 4.8. Діалогове вікно результату підбора параметра
ПРАКТИЧНЕ ЗАВДАННЯ.

 

 

 4.1. Побудувати графік функції відповідно до варіанта:

 

 Варіант 1:  sin(x)e^-2x;   при х [-2; 2];

 Варіант 2:   ;   при х [-2; 2];

 Варіант 3:   ;   при х [-2; 1.5];

 Варіант 4:   ;   при х [-1.5; 1.5];

 Варіант 5:   ;   при х [-1.8; 1.8];

 Варіант 6:   ;   при х [-2; 1.8];

 Варіант 7:     ;  при х [-1.7; 1.5];

 Варіант 8: 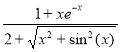   ;  при х [-1.5; 1.8];

 Варіант 9:  ;  при х [-1.4; 1.9];

 Варіант 10: 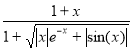 ; при х [-1.4; 1.4].

 

Крок функції вибрати самостійно.

 

 

 

4.2. Побудувати графік функції відповідно до варіанта:

 

Варіант 1: g=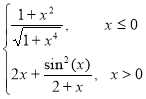 ; при х [-2; 2];

 Варіант 2: g=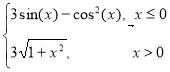 ; при х [-2; 2];

 Варіант 3: g=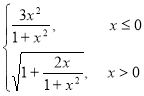 ; при х [-2; 1.5];

 Варіант 4: g=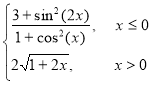 ; при х [-1.5; 1.5];

 Варіант 5: g=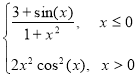 ; при х [-1.8; 1.8];

 Варіант 6: g= ; при х [-2; 1.8];

 Варіант 7:  g= ; при х [-1.7; 1.5];

 Варіант 8:  g=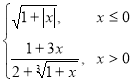 ; при х [-1.5; 1.8];

 Варіант 9: g= ; при х [-1.4; 1.9];

 Варіант 10:  g=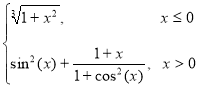 ; при х [-1.4; 1.4].

 

Крок функції вибрати самостійно.

 

 

4.3. Знайти всі корені рівняння:

 

Варіант 1:  x³  + 1,41x² - 5,4724x - 7,380384    = 0

Варіант 2:  x³  + 0,85x² - 0,4317x + 0,043911   = 0

Варіант 3:  x³  - 2,92x² + 1,4355x + 0,791136   = 0

Варіант 4:  x³  - 2,56x² - 1,3251x + 4,395006    = 0

Варіант 5:  x³  + 2,84x² - 5,6064x - 14,766366  = 0

Варіант 6:  x³  - 0,12x² - 1,4775x + 0,191906    = 0

Варіант 7:  x³  + 0,77x² - 0,2513x + 0,016995   = 0

Варіант 8:  x³  + 0,88x² - 0,3999x + 0,037638   = 0

Варіант 9:  x³  + 0,78x² - 0,8269x + 0,146718   = 0

Варіант 10:  x³  + 2,28x² - 1,9347x - 3,907574    = 0

 

 

 

КОНТРОЛЬНІ ПИТАННЯ.

 

1. Для чого використовується майстер діаграм?
2. Навіщо в діаграмі потрібна легенда?
3. Як розташувати діаграму автоматично на окремому листі під назвою «Лист диаграмм»?
4. Які особливості побудови графіку функції з двома умовами?
5. Навіщо використовується функція ЯКЩО (ЕСЛИ, IF)?
6. Які логічні функції MS Excel 2000/XP ви знаєте? Опишіть їх аргументи.
7. Опишіть етапи знаходженя корінь нелінейного рівняння методом підбору параметра.
8. Як задати кількість ітерацій та погрішність у методі підбору параметра?