Практична робота 7:"Табличний процесор Excel"

ПРАКТИЧНА РОБОТА № 7.

 

 Тема: Розв'язання оптимізаційних задач. Лінійна оптимізаційна задача.

 Ціль: Навчитися розв’язувати лінійні оптимізаційні задачі.

 

 

МЕТОДИЧНІ ВКАЗІВКИ.

 

1. Пошук рішення та розв'язання оптимізаційних задач          

 

В MS Excel є потужний інструмент вирішення оптимізаційних задач – Поиск решения (пошук рішення). Пошук рішення є однією із надбудов (add-ins) MS Excel. Якщо в меню Сервис відсутня команда Поиск решения, для її установки необхідно вибрати команду Сервис -> Надстройки. У списку надбудов виберіть Поиск решения і натисніть кнопку ОК.

 

7.2. Лінійна оптимизаційна задача. Постановка завдання про оптимальне виробництво фарб

 

Розглянемо наступне завдання планування виробництва. Фабрика випускає два типи фарб: для внутрішніх (I) і зовнішніх робіт (Е). Продукція обох видів надходить в оптовий продаж; для виробництва  фарб  використовуються два вихідних продукти – А и В. Максимально можливі добові запаси продуктів становлять 6 т й 8 т відповідно. Витрати продуктів А и В на 1 т відповідних фарб приводяться нижче:

 

 

Вихідний продукт	Витрати вихідних продуктів у тоннах на тонну фарби		Максимальний запас, т
	Фарба Е	Фарба I
А	1	2	6
В	2	1	8

 

 

Вивчення ринку збуту показало, що добовий попит на фарбу I ніколи не перевищує попиту на фарбу Е більш ніж на 1 т. Крім того, встановлене, що попит на фарбу I ніколи не перевищує 2 т у добу. 

Оптові ціни однієї тонни фарб рівні: 3000 грн. для фарби Е и 2000 грн. для фарби I.

Яку кількість фарби кожного виду повинна виробляти фабрика, щоб прибуток від реалізації продукції був максимальним?

Для рішення цієї задачі необхідно спочатку побудувати математичну модель. Процес побудови моделі починається з відповіді на наступні три питання:

 

• Для визначення яких величин будується модель (тобто, що є змінними моделі)?
• У чому складається мета, для досягнення якої з множини всіх припустимих значень змінних вибираються оптимальні?
• Яким обмеженням повинні задовольняти невідомі?

 

У нашому випадку фабриці необхідно спланувати обсяг виробництва фарб так, щоб максимізувати прибуток. Тому змінними є:

 

• ХI  - добовий обсяг виробництва фарби I;
• ХЕ - добовий обсяг виробництва фарби Е.

 

Сумарний добовий прибуток від виробництва ХI фарби I та ХЕ фарби Е дорівнює:

 

   Z = 3000XE + 2000XI

 

Метою фабрики є визначення серед всіх припустимих значень ХЕ й ХI таких,  які  максимізують сумарний  прибуток,  тобто   цільову функцію Z.

Перейдемо до обмежень, які накладають на ХЕ й ХI. Обсяг виробництва фарб не може бути негативним.

Отже, ХЕ, ХI ≥ 0.

Витрати вихідного продукту для виробництва обох видів фарб не може перевершувати максимально можливий запас даного вихідного продукту. Таким чином,

 

XE + 2XI ≤ 6

2XE + XI ≤ 8

 

Крім того, обмеження на розмір попиту на фарби мають вигляд:

 

XI - XE ≤ 1

XI ≤ 2

 

Звідси математична модель даної задачі має такий вигляд.

 

Максимізувати:

 

 Z = 3000XE + 2000XI

 

при обмеженнях:

 

XE + 2XI ≤ 6

2XE + XI ≤ 8

XI - XE ≤ 1

XI ≤ 2

ХЕ, ХI ≥ 0

 

Дана модель є лінійною, тому що цільова функція і обмеження лінійно залежать від змінних.

 

7.3. Обробка задачі в MS Excel

 

Перейдемо до введення вихідних даних на робочому листі для вирішення задачі про фарби. Для цього:

 

1.   Відведіть комірки A3 і В3 під значення змінних ХЕ й ХI.

2.   Введіть в комірку C4 функцію цілі:

 

=3000*А3+2000*В3

 

3. Введіть в комірки діапазону А7:А10 ліві частини обмежень, а в комірки діапазону В7:В10 відповідні праві частини обмежень:

 

Комірка  Формула  Комірка  Значення

 

А7   =АЗ+2*В3  B7   6

А8   =2*А3+В3  B8   8

А9   =В3-А3  B9   1

А10   =В3   B10   2

 

 

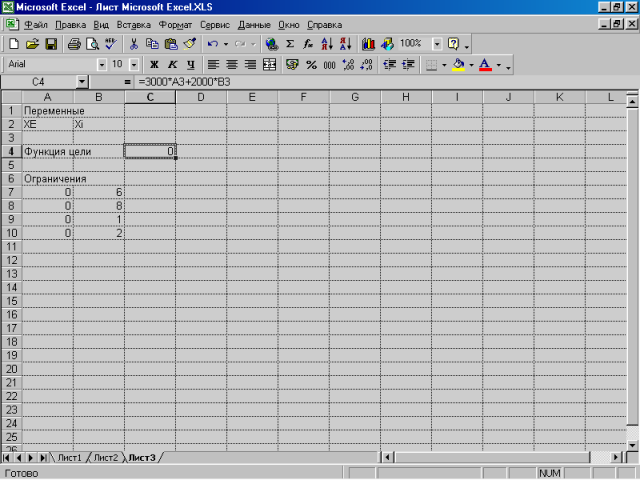
Мал. 7.1. Підготовка до розрахунку оптимізаційної задачі

 

 

7.4. Вирішення задачі про оптимальне виробництво фарб

 

Поставлена задача вирішується за допомогою інструменту  Поиск решения (пошук рішення).

 

1. Виберіть команду Сервис -> Поиск решения. Вікно Поиск решения має такі елементи:                    

 

Поле Установить целевую ячейку – приводиться посилання на комірку з функцією, максимум, мінімум або значення якої пошук рішення буде шукати, змінюючи значення параметрів так, щоб вони задовольняли обмеженням, що на них накладають.

В прикладі із завданням про фарби в поле Установить целевую ячейку уводимо С4.

 

Група Равной - тип взаємозв'язку між рішенням і цільовою коміркою встановлюється шляхом вибору перемикача в цій групі. Для відшукання максимального значення цільової функції вибирається перемикач максимальному значению, мінімального – перемикач минимальному значению; якщо відшукуються значення змінних, для яких значення функції із цільової комірки дорівнює встановленому в поле групи Равной значенню, то вибирається перемикач значению.

У завданні про фарби виберіть перемикач максимальному значению, тому що находимо план виробництва фарб із максимальними прибутками.

 

Поле Изменяя ячейки – приводиться посилання на діапазон комірок або групу діапазонів комірок, відведених під невідомі; значення в цих комірках повинні змінюватися в процесі пошуку рішення задачі так, щоб знайти рішення, що задовольняє заданим обмеженням.

У нашому випадку введемо в поле Изменяя ячейки діапазон А3:В3.

 

Список Ограничения – допускаються обмеження у вигляді рівностей, нерівностей, вимоги того, що невідомі можуть приймати тільки цілі значення, або тільки значення 0 чи 1; обмеження додаються по одному за раз і відображаються у вікні Добавление ограничения, що викликається натисканням кнопки Добавить.

У поле Ссылка на ячейку введіть ліву частину обмежень – А3:В3, у поле Ограничения – праву частину, у нашому випадку – 0.  Список дозволяє задати тип співвідношення між лівою й правою частинами обмеження. У нашому випадку виберіть співвідношення >=. У такий спосіб ми задаємо вимогу незаперечності змінних.

Натисніть кнопку Добавить і за допомогою діалгового вікна Добавление ограничения введіть другу групу обмежень, що накладають на змінні А7:А10 <= В7:В10. Натисніть кнопку ОК для завершення введення обмежень. На екрані знову відобразиться вікно Поиск решения, але тепер вже заповнене. Натисніть  кнопку Параметры – на екрані відобразиться діалогове вікно Параметры поиска решения (мал. 7.3.).

 

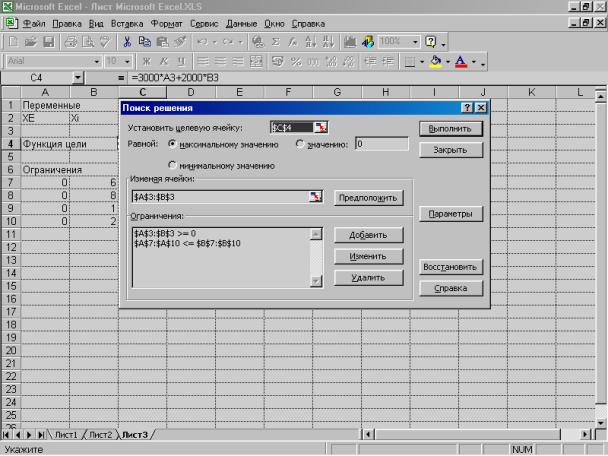
Мал.7.2. Заповнення вікна Поиск решения

 

 

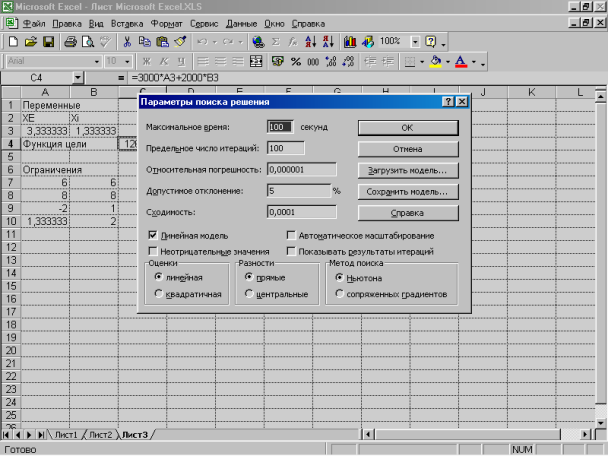
Мал.7.3. Діалогове вікно Параметры поиска решения

2. У вікні Параметры поиска решения можна змінювати умови й варіанти пошуку рішення досліджуваного завдання. Значення та стани елементів керування, використовувані за замовчуванням, підходять для рішення більшості завдань. Опишемо елементи цього вікна:

 

Поле Максимальное время – служить для обмеження  часу, що  відпускається на пошук рішення задачі.

Поле Предельное число итераций – служить для обмеження числа проміжних обчислень.

Поля Относительная погрешность і  Допустимое отклонение– використовуються для завдання точності, з якої шукається рішення. Рекомендується після знаходження рішення з величинами даних параметрів заданих за замовчуванням, повторити обчислення з більшою точністю й меншим припустимим відхиленням та порівняти з початковим методом. Використання подібної перевірки особливо рекомендується для задач із цілочисленими обмеженнями на змінні.

Прапорець Линейная модель – служить для пошуку рішення лінійної задачі оптимізації. У випадку нелінійної задачі цей прапорець повинен бути скинутий, а для лінійної – встановлений, тому що в противному випадку можливе одержання невірного результату.

Прапорець Показывать результаты итераций – служить для припинення пошуку рішення та перегляду результатів окремих ітерацій.

Прапорець Неотрицательные значения – дозволяє встановити нульову нижню границю для тих комірок, що впливають, для яких вона не була зазначена у полі Ограничение діалогового вікна Добавить ограничение.

 Прапорець Автоматичне масштабування – служить для включення автоматичної нормалізації вхідних  і  вихідних значень, що   якісно  розрізняються по величині. Наприклад, максимізація прибутку у відсотках стосовно вкладень, що обчислюються у мільйонах гривень.

 Інші елементи служать для вибору методів пошуку рішення, у більшості випадків їх варто залишати без змін.

 

У нашому випадку встановіть прапорець Линейная модель, а інші значення варто залишити без змін. Натисніть кнопку ОК. На екрані знову відобразиться вікно Поиск решения.

 

3. Натисніть кнопку Выполнить. На екрані відобразиться вікно Результаты поиска решения, у якому буде зазначено, що рішення знайдене (мал. 7.4.).

 

4. Після натискання кнопки ОК, результати будуть внесені в робочий лист.

 

Зі знайденого рішення видно, що оптимальним є виробництво в добу 3,333 т фарби Е та 1,333 т фарби I. Цей обсяг виробництва принесе максимально можливі 12666,67  грн. добового прибутку.

 

 

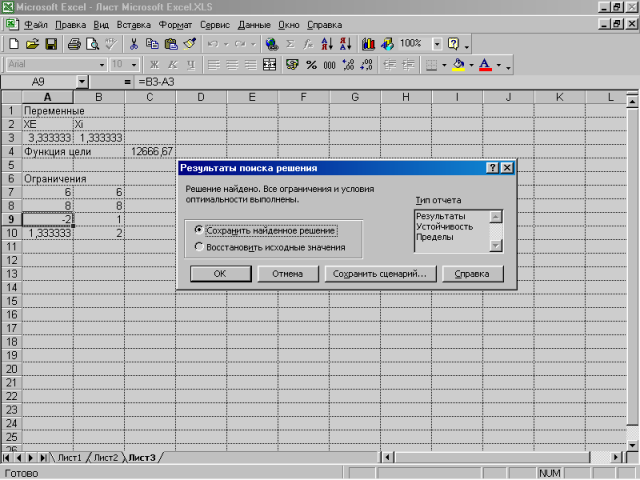
Мал. 7.4. Результати пошуку рішення задачі

 

 

ПРАКТИЧНЕ ЗАВДАННЯ.

 

 7.1. Підприємство електронної промисловості випускає 2 моделі радіоприймачів. Максимальний добовий обсяг виробництва приймачів першого типу - 60 виробів,  другого типу - 75 виробів. На приймач першого типу витрачається х однотипних елементів мікросхем, на приймач другого типу  - у таких же схем. Максимальний запас елементів на складі - Х шт. Прибуток від реалізації приймачів першого типу - 140 грн. і 95 грн. - другого типу. Визначити оптимальний добовий обсяг виробництва обох моделей приймачів відповідно до варіанта:

 

 Варіант 1:  х=5;  y=7;  Х=650;

 Варіант 2:  х=6;  y=9;  Х=900;

 Варіант 3:  х=7;  y=11;  Х=700;

 Варіант 4:  х=8;  y=9;  Х=750;

 Варіант 5:  х=8;  y=10;  Х=800;

 Варіант 6:  х=7;  y=8;  Х=700;

 Варіант 7:  х=6;  y=9;  Х=750;

 Варіант 8:  х=9;  y=12;  Х=900;

 Варіант 9:  х=10;  y=11;  Х=850;

 Варіант 10:  х=7;  y=10;  Х=800.

7.2. Фірма має можливість рекламувати свою продукцію, використовуючи радіо- і телевізійну мережу. Витрати на рекламу в бюджеті фірми обмежені N грн. на місяць. Кожна хвилина радіореклами обходиться в S грн., а хвилина телереклами - W грн. Фірма хотіла б використовувати радіомережу, принаймні, у два рази частіше, ніж мережу телебачення. Досвід показав, що обсяг збуту, що забезпечує кожна хвилина телереклами, в 25 разів більше збуту, забезпечуваного однією хвилиною радіореклами. Визначити оптимальний розподіл коштів, що відпускають щомісяця, між радіо- і телерекламою.

 

Варіант 1:  N=1000; S=5;  Х=100;

Варіант 2:  N=1100; S=6;  Х=110;

Варіант 3:  N=1200; S=7;  Х=120;

Варіант 4:  N=1300; S=8;  Х=130;

Варіант 5:  N=1400; S=9;  Х=140;

Варіант 6:  N=1500; S=8;  Х=150;

Варіант 7:  N=1600; S=7;  Х=160;

Варіант 8:  N=1700; S=6;  Х=150;

Варіант 9:  N=1800; S=5;  Х=140;

Варіант 10:  N=1900; S=7;  Х=130.

 

 

КОНТРОЛЬНІ ПИТАННЯ.

 

1. Як додати в меню MS Excel пункт ”Пошук рішення”?
2. Назвіть три етапи побудови математичної моделі лінійної оптимізаційної задачі?
3. Чому значення обсягу виробництва не може бути негативним?
4. Перелічте елементи діалогового вікна пошуку рішення. Навіщо вони використовуються?
5. Перелічте елементи діалогового вікна параметрів пошуку рішення. Навіщо вони використовуються?
6. Коли потрібно змінювати значення допустимого відхилення та відносної погрішністі у діалоговому вікні параметрів пошуку рішення?