Правильні і неправильні дроби. Порівняння дробів.
Тема. Правильні і неправильні дроби. Порівняння дробів.
Мета: закріпити знання про поняття «правильний дріб», «неправильний дріб», правила порівняння дробів з однаковими знаменниками; відпрацювати навички застосування цих знань під час розв'язання задач.
Тип уроку: засвоєння навичок і вмінь.
Обладнання: таблиця «Правильні і неправильні дроби. Порівняння дробів» (рис. 103).
Хід уроку
І. Перевірка домашнього завдання
№№ 695 і 697 можна перевірити під час фронтального опитування.
Запитання до класу
- Скільки існує дробів, що задовольняють умову задачі?
-
Яким має бути чисельник (знаменник), щоб задовольнити умову: дріб
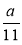 — правильний [дріб
— правильний [дріб 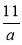 — неправильний].
— неправильний].
- № 699 — один з учнів працює біля дошки: ставить відповідні знаки (дроби заздалегідь записані на дошці вчителем).
- № 701 — вчитель готує картки із записаними на них дробами, а 1 учень біля дошки або за допомогою магнітної дошки, або іншим способом розставляє ці картки так, щоб виконувалась умова задачі.
II. Актуалізація опорних знань
Під час перевірки домашнього завдання формулюються основні означення і правила, вивчені на попередньому уроці. Тому вчителеві достатньо тільки конкретизувати матеріал, поставивши класу запитання.
- Який дріб називається правильним (неправильним)? Наведіть приклади.
- Який дріб більше? Чому?
1) ![]() чи
чи ![]() ; 2)
; 2) ![]() чи
чи ![]() ; 3)
; 3) ![]() чи
чи ![]() .
.
- Що більше:
1) ![]() дм чи 5 см; 2) 74 см чи
дм чи 5 см; 2) 74 см чи ![]() м; 3)
м; 3) ![]() т чи 695 кг; 4)
т чи 695 кг; 4) ![]() год чи 18 хв?
год чи 18 хв?
III. Засвоєння знань. Відпрацювання навичок
Розв'язування вправ №№ 702; 704; 706; 70S (1); 710; 711; 713; додатково задачі 1, 2
№ 702. х < 9, тобто х набуває одного із значень 1, 2, 3 8.
№ 704. х < 6, тобто х набуває одного із значень: 1, 2, ..., 6.
№ 706.
1) 63 : 7 · 9 = 81 (дет.) виготовляє Іван Працелюб
2) 81 – 63 = 18 (дет.) — більше за норму.
Відповідь. 81 деталь; на 18 деталей.
№ 708 (1). ![]() <
< ![]() , тому х < 9, х набуває одного із значень 1, 2, 3,..., 8.
, тому х < 9, х набуває одного із значень 1, 2, 3,..., 8.
№ 710.
1) ![]() неправильний, якщо 4*6 > 476, тобто можливі цифри 7,8,9.
неправильний, якщо 4*6 > 476, тобто можливі цифри 7,8,9.
2) ![]() правильний, якщо 584 < 5*6, тобто можливі цифри 8, 9.
правильний, якщо 584 < 5*6, тобто можливі цифри 8, 9.
№ 711. ![]() правильний, якщо 3b + 2 < 16, тому b = 1, 2, 3, 4.
правильний, якщо 3b + 2 < 16, тому b = 1, 2, 3, 4.
№713.
1) ![]() i
i ![]() правильні, якщо а < 12 і а > 7, тобто а набуває одного із значень 8, 9, 10, 11.
правильні, якщо а < 12 і а > 7, тобто а набуває одного із значень 8, 9, 10, 11.
2) ![]() правильний, якщо а > 3;
правильний, якщо а > 3; ![]() неправильний, якщо а < 6, тому а може набувати одного із значень 4; 5; 6.
неправильний, якщо а < 6, тому а може набувати одного із значень 4; 5; 6.
Додаткові задачі
-
Накресліть координатний промінь і візьміть за одиничний відрізок 12 клітинок. Відмітьте точки: О(0); E(1); А(2); К
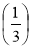 ; М
; М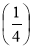 ; N
; N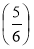 ; Р
; Р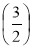 ; S
; S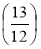 ; Т
; Т 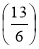 ; С
; С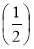 .
.
- Що більше:
1) ![]() год чи
год чи ![]() год; 2)
год; 2) ![]() год чи
год чи ![]() год; 3)
год; 3) ![]() дм чи
дм чи ![]() дм;
дм;
4) ![]() м чи
м чи ![]() дм; 5)
дм; 5) ![]() т чи 400 кг; 6)
т чи 400 кг; 6) ![]() ц чи
ц чи ![]() т?
т?
IV. Підсумок уроку
Учитель ще раз повторює з учнями основні поняття і правила теми (правильний, неправильний дріб, правило порівняння дробів із однаковими знаменниками) і пропонує гру.
Учитель. Зараз я буду називати по одному натуральні числа, які є чисельниками дробів, а вам треба до кожного підібрати інше натуральне число, яке можна було б записати у знаменник дробу, щоб дріб був: а) правильним; б) неправильним; в) більшим за 1; г) меншим за 1; д) більшим за даний дріб; є) меншим за даний дріб тощо.
(Для більшої наочності вчитель може приготувати картки із деякими натуральними числами або навіть записувати числа та умови завдань на дошці.)
V. Домашнє завдання
п. 24, № 707; 709; 712; 714.


про публікацію авторської розробки
Додати розробку
