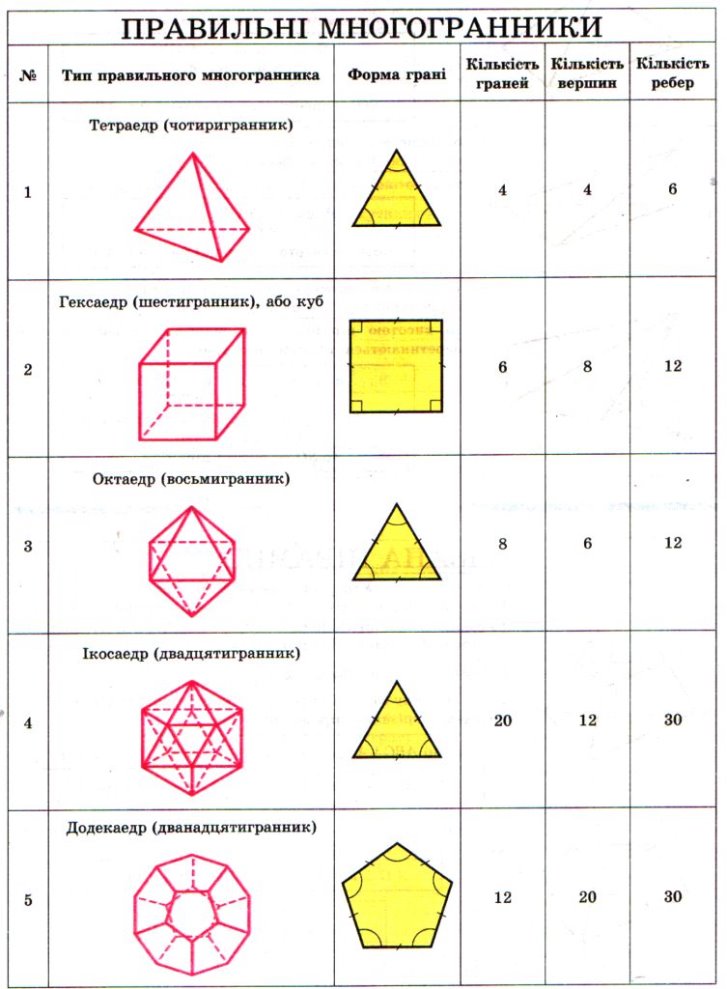
Правильні многогранники
Тетраедр
Гексаедр
 Октаедр
Октаедр
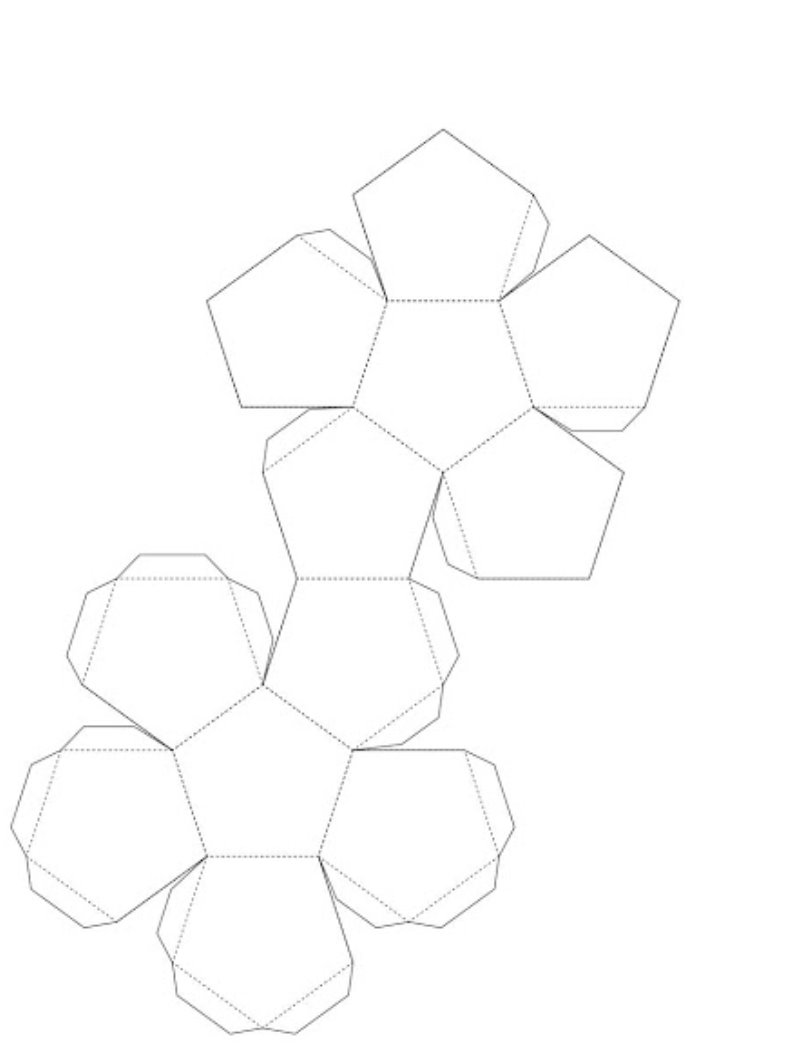 Додекаедр
Додекаедр
Ікосаедр
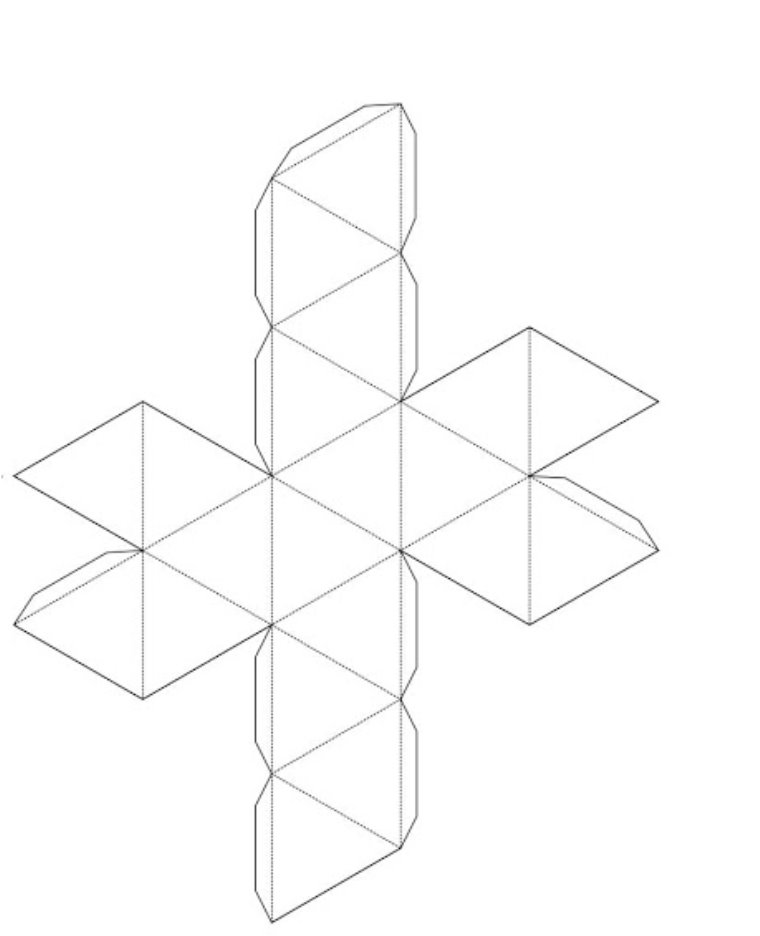
Тема уроку
Правильні многогранники
Формування компетентностей
- Предметна (математична) компетентність: сформувати поняття правильного многогранника; розглянути види правильних многогранників; сформувати вміння розв’язувати задачі на використання поняття правильних многогранників.
- Ключові компетентності:
спілкування державною мовою – уміти доречно та коректно вживати математичну термінологію, зрозуміло формулювати думку, аргументувати, доводити правильність тверджень;
інформаційно – цифрова компетентність – уміння знаходити інформацію, оцінювати її достовірність та ділитися нею з присутніми.
уміння вчитися продовж життя – уміння визначати мету навчальної діяльності, аналізувати, контролювати, коригувати та оцінювати результати своєї навчальної діяльності.
соціальна та громадянська компетентності – уміння аргументувати та відстоювати свою позицію; уміння співпрацювати у команді, вносити свою частку в роботу групи.
Тип уроку: засвоєння нових знань та вмінь.
Міжпредметні зв’язки: біологія, історія, хімія, архітектура, художня культура.
Обладнання: Комп’ютер, мультимедійна презентація, моделі правильних многогранників, роздатковий матеріал.
Епіграф уроку:
Правильних многогранників надзвичайно мало, але цей дуже скромний за кількістю загін зумів пробитися у найбільші глибини різних наук.
Льюїс Керрол
Хід уроку
I. Організаційний момент
(Клас поділено на 5 груп)
Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.
II. Актуалізація опорних знань учнів
Перед початком уроку повторимо все, що нам відомо про призми та піраміди. А оскільки ви поділені групи, то кожна вибере питання, на які буде відповідати.
Приклади питань:
-
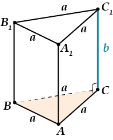 Означення призми.
Означення призми.
- Правильна призма це…
- Пряма призма це …
- Який многокутник може лежати в основі призми?
- Поверхня призми складається …
- Бічна поверхня призми складається …
- Властивості основ призми.
- Які між собою бічні ребра прямої призми?
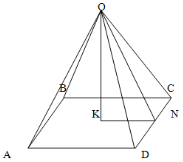 1) Означення піраміди.
1) Означення піраміди.
2) Правильна піраміда це…
3) Пряма піраміда це …
4) Поверхня піраміди складається …
5) Який многокутник може лежати в основі піраміди?
6) Бічна поверхня піраміди складається …
7) Висотою піраміди називається …
8) Яка піраміда називається n-кутною?
Перевірка письмового домашнього завдання здійснюється «за зразком» правильного розв’язання, яке демонструється на дошці.
III. Мотивація навчальної діяльності
Геометрія являє собою могутній інструмент пізнання світу.
 (Демонстрація правильних многогранників, які зустрічаються у природі, архітектурі, біології тощо):
(Демонстрація правильних многогранників, які зустрічаються у природі, архітектурі, біології тощо):



Жодне геометричне тіло не має такої довершеності та краси, як правильні многогранники. «Правильних многогранників так мало, написав колись Льюїс Керролл, - але цей скромний за кількістю загін зумів увійти в самі глибини різних наук». Льюїс Керролл –англійський письменник, математик, філософ та фотограф. Найбільш відомі його роботи – «Аліса в Країні чудес» і «Аліса в Задзеркаллі».
Сьогодні на уроці ми ознайомимося з поняттям правильних многогранників, їх видами та елементами. Знайдемо правильні многогранники у природі.
Тема сьогоднішнього уроку “Правильні многогранники”.
Існує всього 5 правильних многогранників. Назва кожного правильного многогранника походить від грецької назви кількості його граней і слова “грань”. Правильні многогранники мають багату історію, яка пов’язана з таким знаменитими ученими старовини, як Піфагор, Платон, Евклід, Архімед, Кеплер.
IV. Сприйняття і усвідомлення нового матеріалу.
У курсі планіметрії ви познайомилися з правильними многокутниками. Давайте згадаємо означення та властивості таких фігур.
Існує безліч правильних многокутників.
Опуклий многогранник називається правильним, якщо його грані є правильними многокутниками з однією й тією ж кількістю сторін, а в кожній вершині многогранника сходиться одне і те ж число ребер.
Існує п’ять типів правильних опуклих многогранників:
– правильний тетраедр;
– правильний гексаедр (куб);
– правильний октаедр;
– правильний додекаедр;
– правильний ікосаедр.
Насправді, щоб отримати який-небудь правильний многогранник, згідно визначення, в кожній вершині має сходитися однакова кількість граней, кожна з яких є правильним многокутником. Сума плоских кутів многогранного кута повинна бути менше 360о. Нехай k – число плоских кутів, які сходяться в одній вершині многогранника. Перебираючи всі можливі цілі розв’язки нерівностей: 60 k < 360, 90 k < 360, 108 k < 360, можна довести, що правильних многогранників лише п’ять.
А як визначити кількість граней, вершин та ребер?
Цим питанням займався знаменитий математик Л. Ейлер.
У правильного тетраедра грані – правильні трикутники, у кожній вершині збігається по три ребра.
Тетраедр – трикутна піраміда, усі ребра якої рівні.
У куба всі грані – квадрати, у кожній вершині збігається по три ребра.
Куб – прямокутний паралелепіпед з однаковими ребрами.
В октаедра грані – правильні трикутники, у кожній вершині збігається по чотири ребра.
У додекаедра грані – правильні п’ятикутники, у кожній його вершині збігається по три ребра.
В ікосаедра грані – правильні трикутники, у кожній його вершині збігається по п’ять ребер.
V. Цікаві повідомлення учнів.
1) Правильним многогранникам присвячена 13-та книга «Начал» Евкліда. Їх ще називають тілами Платона, так як вони займали особливе місце в філософії Платона про будову світогляду Тетраедр символізував вогонь, ікосаедр – воду, гексаедр – землю, октаедр – повітря. Додекаедр символізував увесь світогляд і рахувався головним. Гармонійні стосунки древні греки вважали основою світогляду, тому чотири стихії були пов’язані такою пропорцією: земля/вода = повітря/вогонь.
Форму додекаедра Платон надавав усьому Всесвіту. Саме тому на репродукції картини С. Далі «Тайна вечеря» зображено Ісуса Христа зі своїми учнями на фоні величезного прозорого додекаедра.

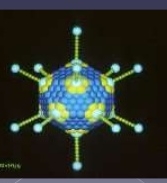
2) Саме ікосаедр опинився в центрі уваги біологів, в їх спірних питаннях щодо форми вірусів. Вірус не може бути зовсім круглим, як вважалося раніше. Щоб встановити його форму, брали різні многогранники, направляли на них світло під тими ж кутами, що й потік атомів на вірус. Виявилося, що тільки один многогранник дає таку ж тінь – це ікосаедр. Його геометричні властивості дозволяють економити генетичну інформацію.
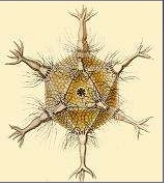
Ікосаедр за формою нагадує скелет одноклітинного організму феодарії.
Ікосаедр має найбільший об’єм при найменшій площі поверхні. Ця властивість допомагає морському організму долати тиск води.
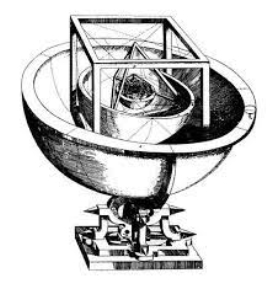
3)Німецький астроном і математик І. Кеплер припустив, що існує зв’язок між п’ятьма правильними многогранниками і шістьма відкритими на той час планетами Сонячної системи. Згідно цьому припущенню в сферу орбіти Сатурна можна вписати куб, в який вписується сфера орбіти Юпітера. В неї, у свою чергу, вписується тетраедр, описаний навколо сфери орбіти Марса. У сферу орбіти Марса вписується додекаедр, в який вписується сфера орбіти Землі. А вона описана навколо ікосаедра. В який вписана сфера орбіти Венери. Сфера цієї планети описана навколо октаедра, в який вписується сфера Меркурія.
Така модель Сонячної системи отримала назву «Космічного кубка» Кеплера.

VІ. Сприйняття та усвідомлення нового матеріалу
Ще піфагорійці у ІV ст. до н. е. займались побудовою правильних многогранників.
Думаю, що і нам буде зробити це не складно.
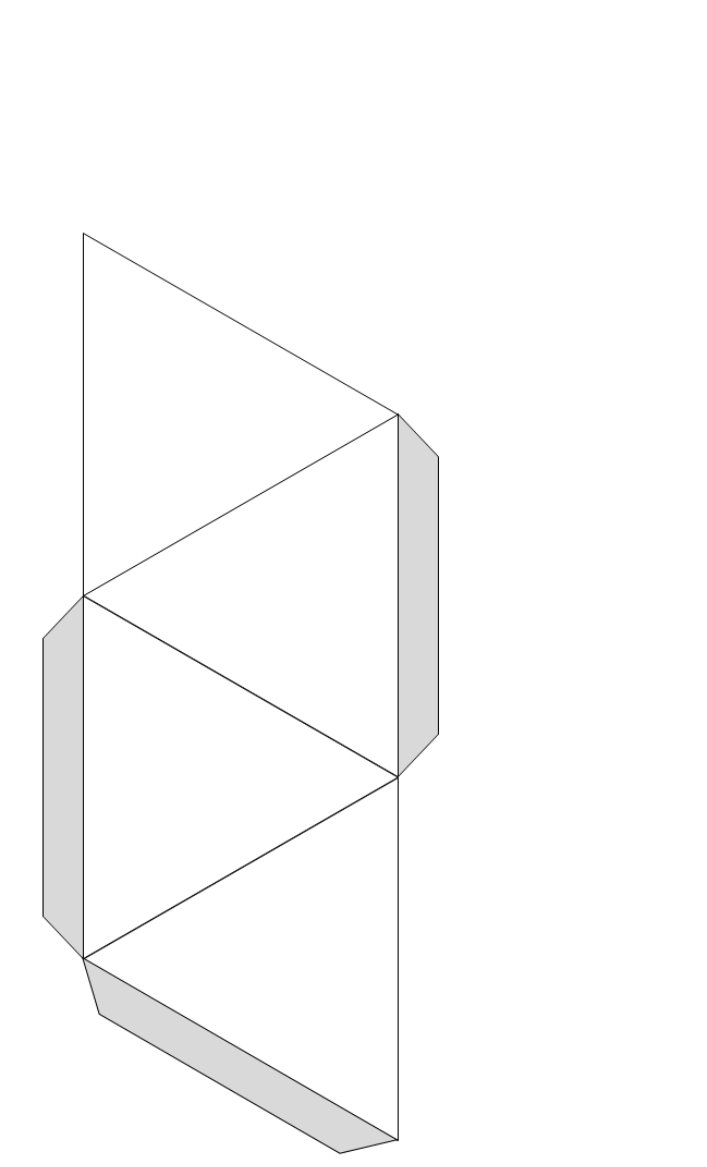
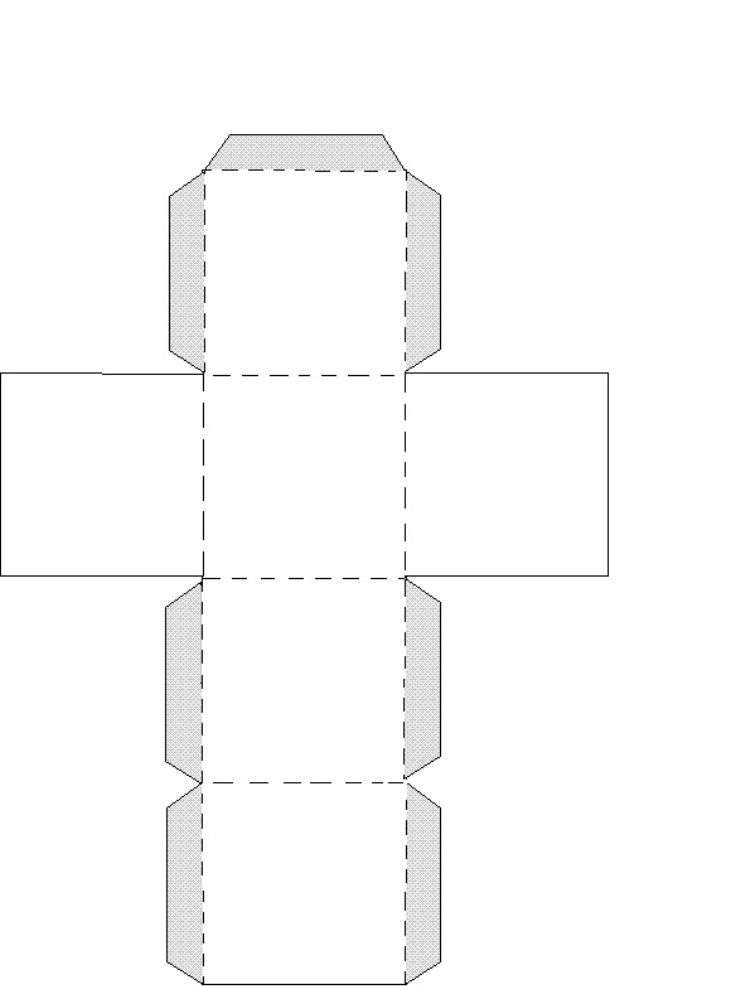
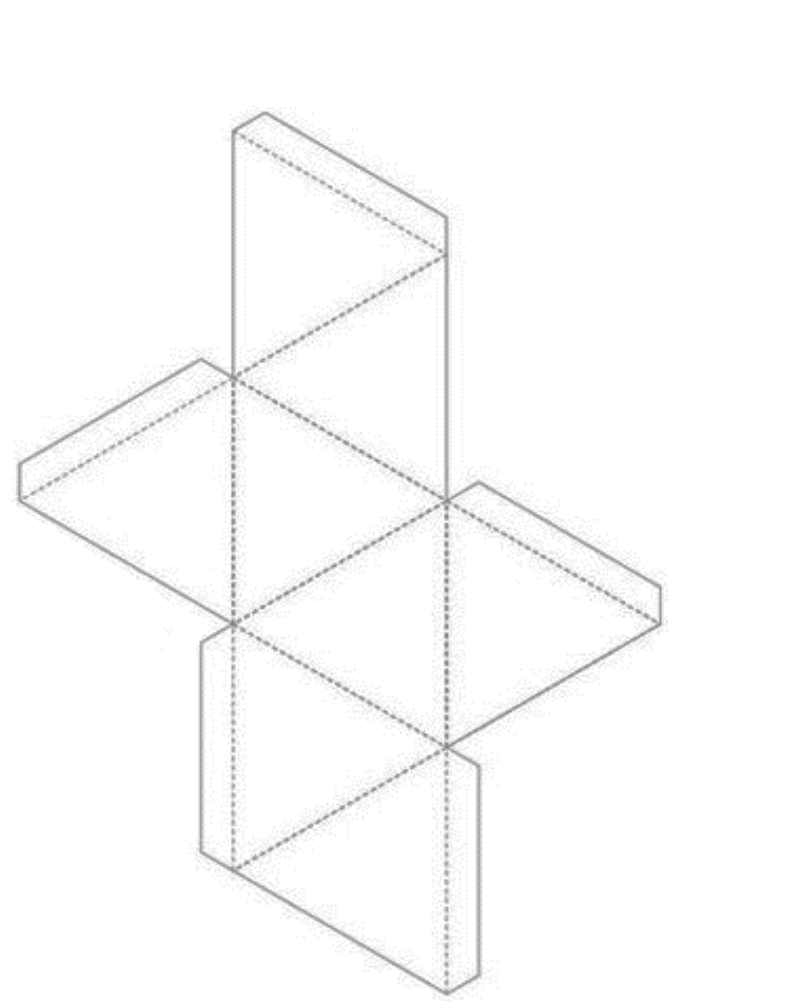
(Клас поділено на групи. Моделі поверхонь правильних многогранників можна склеїти з щільного паперу або картону, скориставшись для цього розгортками цих многогранників. Використовуючи заздалегідь підготовлені розгортки, учні виготовляють правильні многогранники). Після кожній групі пропонується, демонструючи свою модель, заповнити на дошці таблицю:
|
Правильний многогранник |
Вид грані |
Число |
||
|
Вершин |
Граней |
Ребер |
||
|
Тетраедр |
Правильний трикутник |
4 |
4 |
6 |
|
Гексаедр |
Правильний чотирикутник |
6 |
8 |
12 |
|
Октаедр |
Правильний трикутник |
8 |
6 |
12 |
|
Додекаедр |
Правильний п’ятикутник |
12 |
20 |
30 |
|
Ікосаедр |
Правильний трикутник |
20 |
12 |
30 |
Аналізуючи дану таблицю, виникає питання: «Чи нема деякої закономірності у зростанні чисел в кожному стовпці? На перший погляд, ні. В стовпці «вершини» немає навіть стабільного зростання. Кількість вершин то збільшується, то зменшується. В стовпці «ребра» закономірності також не видно. Але можна розглянути суму чисел в двох стовпцях, наприклад, в стовпцях «грані» та «вершини» (Г+В).
|
Правильний многогранник |
Число |
||
|
Граней та вершин (Г + В) |
Ребер (Р) |
||
|
Тетраедр |
4 + 4 = 8 |
6 |
|
|
Гексаедр |
6 + 8 = 14 |
12 |
|
|
Октаедр |
8 + 6 = 14 |
12 |
|
|
Додекаедр |
12 + 20 = 32 |
30 |
|
|
Ікосаедр |
20 + 12 = 32 |
30 |
|
Сформулюємо її так: «Сума числа граней та вершин дорівнює числу ребер, збільшеному на 2», тобто
Г + В = Р + 2.
Отже, ми разом «відкрили» формулу, яка була помічена уже Декартом в 1640 р., а пізніше знову відкрита Ейлером, ім’я якого вона носить. Формула Ейлера дійсна для довільних опуклих многогранників.
VІ. Розв’язування задач.
Кожна група розв’язує свою задачу, яка стосується відповідного правильного многогранника. Після представник від групи захищає розв’язання біля дошки, інші групи можуть задавати питання.
1. «Тетраедр»
Знайдіть ребро правильного тетраедра, площа поверхні якого дорівнює 12 дм2.
2. «Гексаедр»
Під яким кутом з центра куба видно його ребро?
3. «Октаедр»
Під яким кутом із центра правильного октаедра видно його ребро?
4. «Додекаедр»
Знайдіть суму плоских кутів при всіх вершинах додекаедра.
5. «Ікосаедр»
Площа поверхні правильного ікосаедра дорівнює 360 см2. Знайдіть площу однієї грані та ребро ікосаедра.
Додаткова задача для всіх груп:
Основою піраміди є грань куба, а вершиною – його центр. Знайдіть об’єм піраміди, якщо ребро куба дорівнює 3 см.
VII. Підведення підсумків заняття.
Підведення підсумків.
- Що ми вивчали на сьогоднішньому уроці?
- Сформулюйте означення правильного многогранника.
- Скільки існує типів правильних многогранників?
VIIІ. Домашнє завдання.


про публікацію авторської розробки
Додати розробку
