Презентація - ЗНО 2007 (Фізика)

ЗНО 2007фізика

№1. Тіло рухається у площині x. Oy. Визначте, яка з наведених на рисунку залежностей свідчить про прямолінійний рух тіла. Х

№2. Для прямолінійного руху за графіком залежності проекції прискорення тіла від часу визначте графік залежності проекції швидкості цього тіла від часу. 𝜗0х=5мс. X

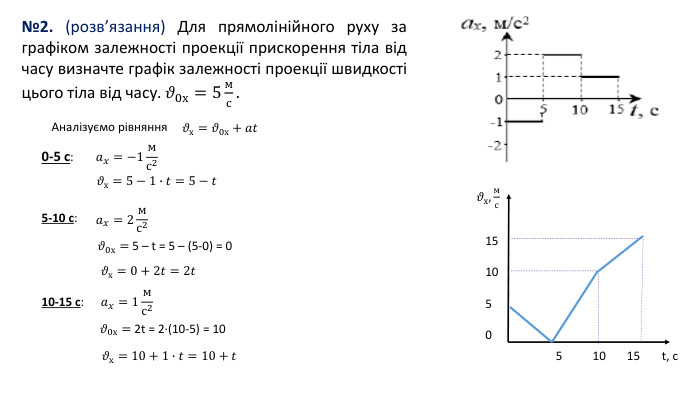
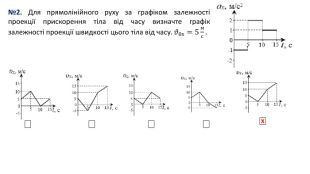
№2. (розв’язання) Для прямолінійного руху за графіком залежності проекції прискорення тіла від часу визначте графік залежності проекції швидкості цього тіла від часу. 𝜗0х=5мс. 0-5 с:𝑎𝑥=−1мс2 𝜗х=𝜗0х+𝑎𝑡 Аналізуємо рівняння𝜗х=5−1∙𝑡=5−𝑡 5-10 с:𝑎𝑥=2мс2 10-15 с:𝑎𝑥=1мс2 𝜗0х= 5 – t = 5 – (5-0) = 0 𝜗х=0+2𝑡=2𝑡 𝜗0х= 2t = 2∙(10-5) = 10  𝜗х=10+1∙𝑡=10+𝑡 t, c𝜗х,мс  5 10 1515 10 5 0

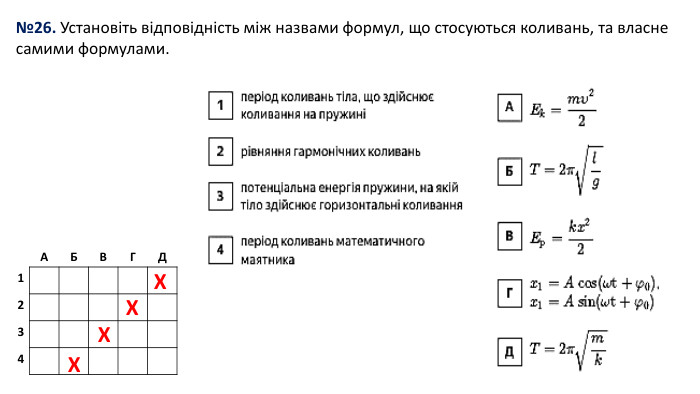
№3. Два однакові диски обертаються навколо своїх осей. Точки на краю першого диска мають в 4 рази менше нормальне прискорення, ніж точки на краю другого диску. Знайдіть відношення періоду обертання першого диску до періоду обертання другого диска. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД420,50,2516 Дано:𝑎д1=14𝑎д2 𝑇1𝑇2−? 𝑎д1=𝜗12𝑅1=2𝜋𝑅1𝑇12𝑅1=4𝜋2𝑅12𝑇12𝑅1=4𝜋2𝑅1𝑇12 𝑎д2=𝜗22𝑅2=2𝜋𝑅2𝑇22𝑅2=4𝜋2𝑅22𝑇22𝑅2=4𝜋2𝑅2𝑇22 За умовою 𝑎д1=14𝑎д2  4𝜋2𝑅1𝑇12=144𝜋2𝑅2𝑇22 (за умовою 𝑅1=𝑅2) 𝑇12=4𝑇22 𝑇1=2𝑇2 𝑇1𝑇2=2 Відповідь: 𝑇1𝑇2=2  

№4. Укажіть, у якому з перелічених нижче випадків спостерігається явище інерції. А) камінь вільно падаєБ) артилерійський снаряд летить з гармати у ціль по параболіВ) автомобіль рухається рівномірно прямолінійно. Г) супутник рухається по орбітіД) в момент старту ракети космонавт відчуває перевантаження

№5. Визначте, яку загальну масу має смугастий циліндричний вантаж. Призматичні вантажі на фото мають масу по 100 г кожен.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД300 г200 г100 г150 г250 г

№5. Дано:m1=300 гm2=100 гmх-?𝑚1𝑔 𝑚2𝑔 𝑚𝑥𝑔 𝑙1 𝑙2 𝑙𝑥 Запишемо умову рівноваги важеля𝑀1=𝑀2+𝑀𝑥 𝑚1𝑔𝑙1=𝑚2𝑔𝑙2+𝑚𝑥𝑔𝑙𝑥 Згідно рисунка визначаємо плечі сил𝑚1𝑔4𝑙0=𝑚2𝑔2𝑙0+𝑚𝑥𝑔4𝑙0 4𝑚1=2𝑚2+4𝑚𝑥 4𝑚𝑥=4𝑚1+2𝑚2 𝑚𝑥=4𝑚1−2𝑚24 𝑚𝑥=4∙300 г−2∙100 г4=250 г Відповідь: 𝑚𝑥=250 г 

№6. Учні на уроці фізкультури грають у волейбол. Визначте максимальну висоту (у метрах) відносно рук гравців, якої досягає м’яч, якщо відомо, що у польоті між двома ударами він перебуває 2 с. Вважайте, що 𝑔=10мс2 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД20 м10 м5 м2,5 м1,25 м. Дано:t = 2 cg = 10мс2 h - ?𝑡=2𝜗0𝑠𝑖𝑛𝛼𝑔 h=𝜗02𝑠𝑖𝑛2𝛼2𝑔 𝑡2=4𝜗02𝑠𝑖𝑛2𝛼𝑔2 h=𝜗02𝑠𝑖𝑛2𝛼2𝑔 𝜗02𝑠𝑖𝑛2𝛼=𝑡2𝑔24 𝜗02𝑠𝑖𝑛2𝛼=2𝑔h 2𝑔h=𝑡2𝑔24 h=𝑡2𝑔8 h=2 𝑐2∙10мс28 = 5 м Відповідь: h = 5 м

№7. На рисунку в координатах p. V зображений замкнутий цикл 1 —> 2 —>3 —>4, здійснений незмінною масою газу (лінія 2 —> 3 – частина гіперболи). Визначте, який вигляд має цей цикл у координатах p. T. X

№7.1 —> 2: p=const – ізобарний процес𝑉1𝑇1=𝑉2𝑇2 Отже, 𝑉1↑𝑖 𝑇1↑ p. T122 —>3: T=const – ізотермічний процес𝑝2𝑉2=𝑝3𝑉3 Отже, 𝑝2↓𝑖 𝑉2↑ 33 —> 4: p=const – ізобарний процес𝑉3𝑇3=𝑉4𝑇4 Отже, 𝑉3↓𝑖 𝑇3↓ 44 —> 1: V=const – ізохорний процес𝑝4𝑇4=𝑝1𝑇1 Отже, 𝑝4↑𝑖 𝑇4↑ 

№8. На рисунку показані різні циклічні процеси, здійснені тією самою масою газу. Визначте, під час якого циклу газ виконав найбільшу роботу.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД

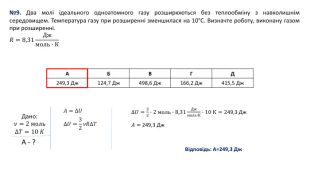
№9. Два молі ідеального одноатомного газу розширюються без теплообміну з навколишнім середовищем. Температура газу при розширенні зменшилася на 10°С. Визначте роботу, виконану газом при розширенні. 𝑅=8,31 Джмоль∙К Дано:𝜈=2 моль∆𝑇=10 𝐾 A - ?𝐴=∆𝑈 ∆𝑈=32𝜈𝑅∆𝑇 ∆𝑈=32∙2 моль∙8,31 Джмоль∙К∙10 К=249,3 Дж 𝐴= 249,3 Дж Відповідь: А=249,3 Дж{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД249,3 Дж124,7 Дж498,6 Дж166,2 Дж415,5 Дж

№10. Стародавні майстри навчилися виготовлювати зі слабко обпаленої глини посудини, в яких вода залишилася прохолодною навіть у спеку. Позначте явище, яке спричиняло охолодження води. А) конвекція в повітріБ) охолодження води внаслідок випромінювання. В) конвекція у водіГ) охолодження води внаслідок випаровування. Д) дифузія повітря крізь стінки посудини

№11. На рисунку показано взаємне розташування трьох однакових за модулем точкових зарядів. Укажіть напрямок результуючої сили, що діє на другий заряд з боку першого та третього зарядів. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД

№12. Визначте, яку роботу виконає поле при переміщенні точкового заряду 10 н. Кл з точки, потенціал якої 700 В, в точку з потенціалом 300 В. Дано: q = 10 н. Кл𝜑1=700 В𝜑2=300 В А - ?А=𝑞(𝜑1−𝜑2) 10 н. Кл = 10∙10-9 Кл = 10-8 Кл. А=10−8 Кл700 В−300 В=400∙ 10−8 Дж = 4 ∙ 10−6 Дж = 4 мк. Дж  Відповідь: А = 4 мк. Дж{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 4 мк. Дж 3 мк. Дж 100 мк. Дж 10 мк. Дж 7 мк. Дж. Х

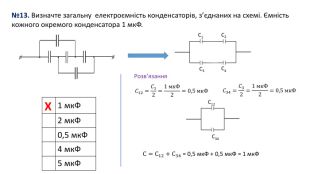
№13. Визначте загальну електроємність конденсаторів, з’єднаних на схемі. Ємність кожного окремого конденсатора 1 мк. Ф.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 1 мк. Ф 2 мк. Ф 0,5 мк. Ф 4 мк. Ф 5 мк. ФРозв’язання. ХC1 C2 C3 C4𝐶12=𝐶12=1 мк. Ф2=0,5 мк. Ф 𝐶34=𝐶32=1 мк. Ф2=0,5 мк. Ф C34 C12 С=С12+С34 = 0,5 мк. Ф + 0,5 мк. Ф = 1 мк. Ф 

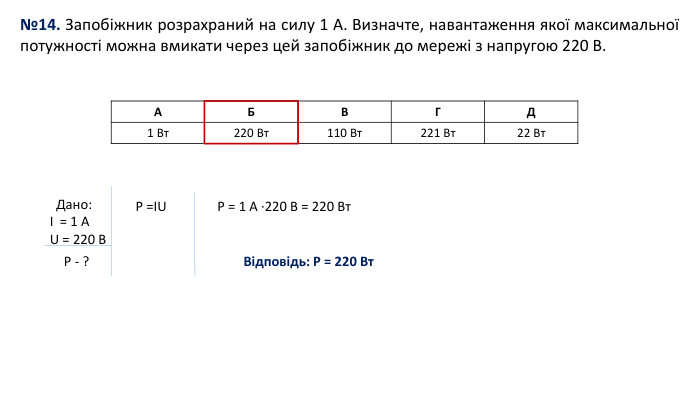
№14. Запобіжник розрахраний на силу 1 А. Визначте, навантаження якої максимальної потужності можна вмикати через цей запобіжник до мережі з напругою 220 В. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД1 Вт220 Вт110 Вт221 Вт22 Вт Дано:І = 1 АU = 220 BP - ?P =IUP = 1 A ∙220 B = 220 Вт. Відповідь: Р = 220 Вт

№15. Укажіть, яке з перелічених явищ називається термоелектронною емісією. А) Іонізація нейтральних атомів при зіткненні з електронами. Б) Вибивання електронів з катоду при бомбардуванні його додатними іонами. В) Випромінювання електронів катодом при його нагріванніГ) Збільшення енергії вільних електронів під впливом електричного поля. Д) Світіння розрідженого газу при проходженні через нього електричного струму

№16. Укажіть, у якому степені одиниця часу входить до одиниці магнітної індукції, вираженої через основні одиниці СІ.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД+2+1-1-2 Одиниця часу не входить до одиниці магнітної індукції, вираженої через основні одиниці СІ.1 спосіб. В=Н∙м. А∙м2=кг∙м. А∙с𝟐=кг∙м∙А−1с−𝟐 𝐵=𝑀𝐼𝑆 2 спосіб𝐵=𝐹𝑎𝐼𝑙 В=НА∙м=кг∙м. А∙м∙с𝟐=кг∙м∙А−1с−𝟐 

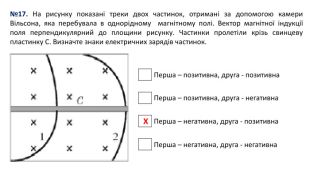
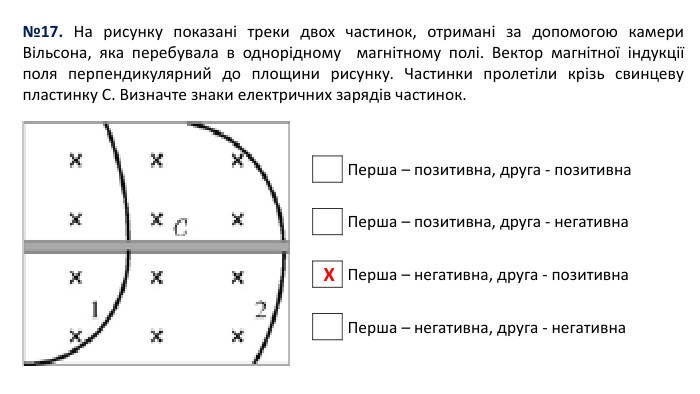
№17. На рисунку показані треки двох частинок, отримані за допомогою камери Вільсона, яка перебувала в однорідному магнітному полі. Вектор магнітної індукції поля перпендикулярний до площини рисунку. Частинки пролетіли крізь свинцеву пластинку С. Визначте знаки електричних зарядів частинок.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Перша – позитивна, друга - позитивна Перша – позитивна, друга - негативна Перша – негативна, друга - позитивна Перша – негативна, друга - негативна Х

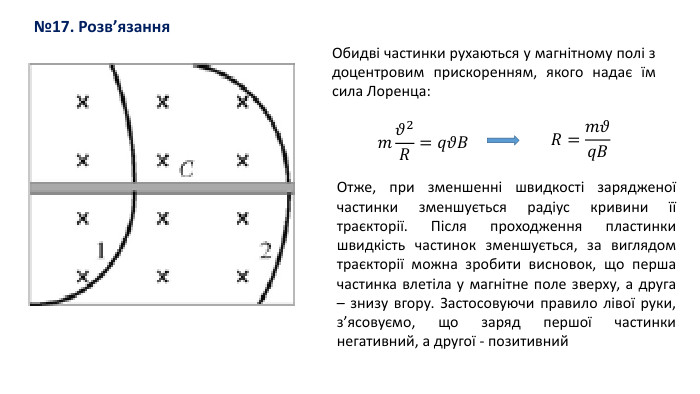
№17. Розв’язання. Обидві частинки рухаються у магнітному полі з доцентровим прискоренням, якого надає їм сила Лоренца: 𝑚𝜗2𝑅=𝑞𝜗𝐵 𝑅=𝑚𝜗𝑞𝐵 Отже, при зменшенні швидкості зарядженої частинки зменшується радіус кривини її траєкторії. Після проходження пластинки швидкість частинок зменшується, за виглядом траєкторії можна зробити висновок, що перша частинка влетіла у магнітне поле зверху, а друга – знизу вгору. Застосовуючи правило лівої руки, з’ясовуємо, що заряд першої частинки негативний, а другої - позитивний

№18. Після розмикання кола живлення котушки з індуктивністю 2 Гн на клемах вимикача виникла ЕРС самоіндукції 300 В. Сила струму до розмикання кола становила 1,5 А. Вважаючи, що сила струму в колі змінювалась рівномірно, визначте час існування струму в котушці після розмикання кола. Дано: Ei = 300 B L = 2 Гн𝐼1=1,5 𝐴  𝐼2=0 𝐴  ∆𝑡− ? Ei = −𝐿∆𝐼∆𝑡 Ei = −𝐿𝐼2−𝐼1∆𝑡 ∆𝑡=−𝐿(𝐼2−𝐼1) Ei ∆𝑡=−2 Гн∙0 А−1,5 А300 В=10−2 с=10∙10−3с=10 мс Відповідь: ∆𝑡 = 10 мс Відповідь: 10

№19. Частота хвилі 4 Гц, а швидкість її поширення дорівнює 16 м/с. Визначте її довжину. Дано:𝜈=4 Гц𝜗=16мс λ - ?𝜆=𝜗𝑇=𝜗𝜈 𝜆=16мс41с=4 м Відповідь: 𝜆= 4 м {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД0,25 м0,5 м1 м4 м64 м

№20. Правильно продовжте твердження: під час незатухаючих електромагнітних коливань, у момент, коли конденсатор має максимальний заряд, максимального значення досягає А) повна енергія електромагнітних коливань. Б) енергія магнітного поля. В) енергія електричного поля. Г) частота коливань. Д) ємність контуру

№21. Визначте кут падіння променя α на поверхню, що розділяє два середовища, якщо заломлений і відбитий промені утворюють кут 90°. Показник заломлення другого середовища відносно першого – n. А) α = n tg n. Б) α = n arctg n В) α=1arctg n. Г) α = arctg n Д) α = ctg n   Дано:𝜃=90° n α - ?θαβγ𝑛=𝑠𝑖𝑛𝛼𝑠𝑖𝑛𝛾 𝑛=𝑠𝑖𝑛𝛼sin⁡(90°−𝛼)=𝑠𝑖𝑛𝛼𝑐𝑜𝑠𝛼=𝑡𝑔𝛼 𝛼=arctg⁡(𝑛) 𝛾=180°−𝜃−𝛽 𝛾=180°−90°−𝛼 𝛾=90°−𝛼 𝛽=𝛼  i. За законом відбивання

№22. У деяку точку простору приходять дві когерентні світлові хвилі з різницею ходу 1,2 мкм. Визначте, якою може бути довжина хвилі (із запропонованих варіантів), щоб у цій точці спостерігався інтерференційний максимум. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД450 нм525 нм600 нм675 нм720 нм{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД450 нм675 нм𝛿=𝑛△ℓ  Дано:∆ℓ=1,2 мкм 𝜆 − ? Уважаємо, що світло поширюється у повітрі (n=1). Оптична різниця ходу хвиль Умова інтерференційних максимумів𝛿=2𝑘𝜆2=𝑘𝜆 𝜆=𝛿𝑘=𝑛△ℓ𝑘 При k=1𝜆=1∙1,2∙10−6м1=1,2∙10−6м=1200 нм При k=2𝜆=1∙1,2∙10−6м2=0,6∙10−6м=600 нм При k=3𝜆=1∙1,2∙10−6м3=0,4∙10−6м=400 нм В наведених відповідях шукаємо відповідне числове значення. Підходить𝜆= 600 нм 

№23. Укажіть співвідношення між частотою випромінювання 𝜈, що падає на метал, і червоною межею фотоефекту 𝜈𝑚𝑖𝑛, якщо максимальна кінетична енергія фотоелектронів у чотири рази менша, ніж робота виходу.  {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД𝜈=1,25𝜈𝑚𝑖𝑛𝜈=2𝜈𝑚𝑖𝑛𝜈=2,5𝜈𝑚𝑖𝑛𝜈=3𝜈𝑚𝑖𝑛𝜈=0,25𝜈𝑚𝑖𝑛{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД Дано:𝐸к макс=Авих4 𝜈𝜈𝑚𝑖𝑛 − ? h𝜈=𝐴вих+𝑚𝜗𝑚𝑎𝑥22 h𝜈=𝐴вих+𝐸к макс=𝐴вих+Авих4=5 Авих4 h𝜈=5h𝜈𝑚𝑖𝑛4=1,25h𝜈𝑚𝑖𝑛  𝜈=1,25𝜈𝑚𝑖𝑛  Відповідь: 𝜈=1,25𝜈𝑚𝑖𝑛  

№24. Визначте, як змінюються порядковий номер (Z) елемента в періодичній системі та його масове число (А) при випромінюванні альфа-частинки. А) Z збільшується на одиницю, А залишається незмінним. Б) Z і А зменшуються на одиницю. В) Z зменшується на дві одиниці, А зменшується на чотири одиниціГ) Z і А залишаються незмінними. Д) Z збільшується на дві одиниці, А зменшується на чотири одиниці

№25. Визначте енергетичний вихід ядерної реакції 37𝐿𝑖+12𝐻→48𝐵𝑒+01𝑛, якщо енергія зв’язку ядра ізотопу Берилію 56,4 Ме. В, ізотопу Літію 39,2 Ме. В, Дейтерію 2,2 Ме. В. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД15 Ме. В19,4 Ме. В97,8 Ме. В93,4 Ме. В12,6 Ме. В{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД15 Ме. В Дано:𝐸зв𝐿𝑖=39,2 Ме. В 𝐸вих− ? 𝐸зв𝐻=2,2 Ме. В 𝐸зв𝐵𝑒=56,4 Ме. В Енергія виходу ядерної реакції можна обчислити через енергію зв’язку ядер. Cумарна енергія зв’язку ядер до реакції𝐸зв1=𝐸зв𝐿𝑖+𝐸зв𝐻 Eнергія зв’язку ядер після реакції𝐸зв2=𝐸зв𝐵𝑒 01𝑛 - нейтрон енергії зв’язку ядер не маєУВАГА!𝐸вих=𝐸зв2−𝐸зв1=𝐸зв𝐵𝑒−𝐸зв𝐿𝑖−𝐸зв𝐻 𝐸вих=56,4 Ме. В−39,2 Ме. В−2,2 Ме. В = 15 Ме. В Відповідь: 𝐸вих= 15 Ме. В 

№26. Установіть відповідність між назвами формул, що стосуються коливань, та власне самими формулами.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД1234 ХХХХ

№27. Установіть відповідність між прізвищами видатних учених та їх науковим доробком. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД1234 ХХХХ

№28. По паралельних дорогах в одному напрямку рухається поїзд довжиною 100 м та маленький легковий автомобіль. Швидкість поїзда дорівнює 54 км/год, швидкість автомобіля 72 км/год. Визначте, скільки часу знадобиться автомобілю, щоб випередити поїзд (проїхати від останнього до першого вагона). Відповідь запишіть у секундах. Відповідь: ______20 Дано:𝑙=100 м𝜗1=54кмкм𝜗2=72кмкм t - ?𝑡=𝑙𝜗 54кмкм=15мс 72кмкм=20мс 𝜗=𝜗2−𝜗1 𝜗=20мс−15мс = 5мс 𝑡=100 м5мс =20 с Відповідь: t = 20 c

№29. Bизначте, у скільки разів треба збільшити потужність двигуна водяного насоса, щоб він через трубу такого самого перерізу за одиницю часу подавав утричі більше води. Воду вважайте ідеальною рідиною. Труба горизонтальна. Відповідь: 27 Дано: S1 = S2𝑉2=3𝑉1𝑡1= t2 𝑃2𝑃1−? Потужність визначається за формулою 𝑃=𝐴𝑡 , де А=𝐸к=𝑚𝜗22 Так як 𝑉2=3𝑉1, то m2 = 3m1 ℓ Об’єм визначається. S𝑉=𝑆ℓ=𝑆𝜗𝑡 𝑆𝜗2𝑡2=3𝑆𝜗1𝑡1 𝜗2=3𝜗1 𝑃2𝑃1=𝑚2𝜗222∙𝑡2𝑚1𝜗122∙𝑡1=3𝑚1(3𝜗1)2𝑚1𝜗12=27 

№30. З балона випустили 2 г газу, в результаті чого тиск у ньому знизився на 10%. Визначте (у м3) місткість балона, якщо густина газу в початковий момент була 0,2 кг/ м3. Температура газу в балоні не змінювалася. Дано: Δm = 2 г𝑝2=0,9𝑝1𝜌=0,2 кгм3 𝑇1=𝑇2=𝑇 V - ?Відповідь: __0,1__𝜌=𝑚𝑉 𝑉=𝑚𝜌 10,9=𝑚1𝑚1−∆𝑚 𝑚1−∆𝑚=0,9𝑚1 𝑚1−0,9𝑚1=∆𝑚 0,1𝑚1=∆𝑚 𝑚1=10∆𝑚 𝑉=10∆𝑚𝜌=10∙2∙10−3кг0,2 кгм3=0,1м3 𝑝1𝑉=𝑚1𝑀𝑅𝑇 𝑝2𝑉=𝑚2𝑀𝑅𝑇 𝑝1𝑉𝑝2𝑉=𝑚1𝑀𝑅𝑇𝑚2𝑀𝑅𝑇 𝑝1𝑝2=𝑚1𝑚2 𝑝10,9𝑝1=𝑚1𝑚1−∆𝑚 𝑚2=𝑚1−∆𝑚 Нехай 𝑚=𝑚1 За умовою

№31. У капілярній трубці радіусом 0,5 мм рідина піднялась на 11 мм. Визначте густину даної рідини, якщо її коефіцієнт поверхневого натягу 0,022 Н/м. Важайте, що g=10 м/с2. Відповідь: ______800 Дано:r = 0,5 ммh = 11 мм𝜎=0,022 Нм𝑔=10 мс2 ρ - ?h=2𝜎𝜌𝑔𝑟 𝜌=2𝜎𝑔𝑟h 0,5 мм = 0,5∙10-3 м11 мм = 11∙10-3 м𝜌=2∙0,022 Нм10мс2∙0,5∙10−3 м ∙11∙10−3 м =800кгм3 Відповідь: 𝜌=800кгм3 

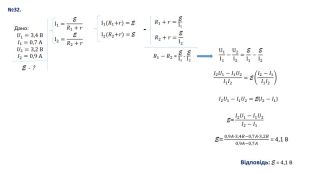
№32. На рисунку зображене електричне коло, що складається з джерела постійного струму (1), вимикача (2), реостата (3), вольтметра (4) й амперметра(5). Коли замкнули електричне коло, покази приладів установилися, як на рисунку І. Коли повзунок реостата перемістили, покази приладів змінилися, як на рисунку ІІ. Визначте (у вольтах) ЕРС джерела струму.

№32. Дано:𝑈1=3,4 В𝐼1=0,7 А𝑈2=3,2 В𝐼2=0,9 А E - ?I1=E𝑅1+𝑟 I2=E𝑅2+𝑟 I1(𝑅1+𝑟)= E I2(𝑅2+𝑟)= E 𝑅1+𝑟=EI1  𝑅2+𝑟=EI2 -𝑅1−𝑅2 = EI1 - EI2 U1 I1−U2 I2=EI1 − EI2 𝐼2𝑈1−𝐼1𝑈2𝐼1𝐼2=E𝐼2−𝐼1𝐼1𝐼2 𝐼2𝑈1−𝐼1𝑈2=E(𝐼2−𝐼1) E=𝐼2𝑈1−𝐼1𝑈2𝐼2−𝐼1 E=0,9𝐴∙3,4𝐵−0,7𝐴∙3,2𝐵0,9𝐴−0,7𝐴 = 4,1 B Відповідь: E = 4,1 В 

№33. Визначте індуктивність котушки, якщо відомо, що по ній протікає струм 20 А, а енергія магнітного поля котушки становить 100 Дж. Відповідно подайте в генрі. Відповідь: _______ 0,5 Дано: I = 20 AW = 100 Дж. L - ?𝑊=𝐿𝐼22 𝐿=2𝑊𝐼2 𝐿=2∙100 Дж(20 А)2=200400 Гн=0,5 Гн Відповідь: L = 0,5 Гн

№34. До електромережі під’єднаний знижувальний трансформатор, коефіцієнт трансформації якого дорівнює 5. Опір вторинної обмотки трансформатора дорівнює 0,4 Ом, а опір корисного навантаження 4 Ом. Визначте напругу в мережі живлення, до якої під’єднаний трансформатор, якщо напруга на корисному навантаженні дорівнює 40 В. Опором первинної обмотки знехтуйте. Відповідь подайте у вольтах. Відповідь: ______ 220 Дано:k = 5𝑅об=0,4 Ом𝑅н=4 Ом𝑈н=40 В 𝑈1− ? 𝑈1𝑈2=𝑘 𝑈1=𝑘𝑈2 𝑈2=𝑈об+𝑈н 𝑈об=𝐼2𝑅об 𝐼2=𝑈н𝑅н 𝐼2=40 В4 Ом=10 А 𝑈об= 10 А∙0,4 Ом = 4 В 𝑈2=4 В+40 В = 44 В 𝑈1=5∙44 В=220 В Відповідь: 𝑈1=220 В  

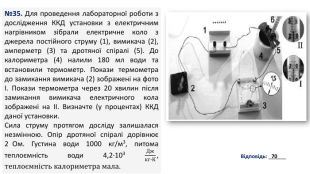
№35. Для проведення лабораторної роботи з дослідження ККД установки з електричним нагрівником зібрали електричне коло з джерела постійного струму (1), вимикача (2), амперметр (3) та дротяної спіралі (5). До калориметра (4) налили 180 мл води та встановили термометр. Покази термометра до замикання вимикача (2) зображені на фото І. Покази термометра через 20 хвилин після замикання вимикача електричного кола зображені на ІІ. Визначте (у процентах) ККД даної установки. Сила струму протягом досліду залишалася незмінною. Опір дротяної спіралі дорівнює 2_Ом. Густина води 1000 кг/м3, питома теплоємність води 4,2∙103 Джкг∙К,  теплоємність калориметра мала. Відповідь: ______70

№35. Дано:m= 180 мл𝑡1=20℃𝑡2=25℃I = 1,5 At = 20 хв. R = 2 Ом𝜌=1000кгм3с = 4200 Джкг∙℃  𝜂 − ? 𝜂=Ак. Аз100% Ак=𝑄=𝑐𝑚(𝑡2−𝑡1) 𝐴з=𝐼2𝑅𝑡 - Корисна робота- Затрачена (повна) робота𝑚=𝜌𝑉 Ак=𝑄=𝑐𝜌𝑉(𝑡2−𝑡1) 𝜂=𝑐𝜌𝑉(𝑡2−𝑡1) 𝐼2𝑅𝑡 100% 180 мл = 180 cм3 = 180∙10-6 м320 хв = 20∙60 с = 1200 с𝜂=4200 Джкг∙℃∙1000кгм3∙180∙10−6 м3 (25℃−20℃) (1,5 А)2∙2 Ом∙1200 с 100% = 70% 

Кінець