Позакласний захід "Конференція з тригонометрії"

Математична конференція для учнів 10 класу

Тема: Тригонометрія. Історичні аспекти та практичне використання

Мета: познайомити учнів з історією виникнення та розвитку тригонометрії. Розвивати інтерес до тригонометрії як до галузі математики, що має велике практичне значення та використовується у багатьох галузях діяльності людини.

План конференції

1. Історичні витоки тригонометрії та її становлення.
2. Тригонометрія  середніх віків.
3. Тригонометрія навколо нас.

Хід конференції

1. Історичні витоки тригонометрії та її становлення.

 

 

Зародки тригонометрії можна знайти  у математичних рукописах стародавнього Єгипту, Вавилона і стародавнього Китаю.

56-а задача з папірусу Рінда (II тис. до н. е.) пропонує знайти нахил піраміди, висота якої дорівнює 250 ліктів, а довжина сторони основи — 360 ліктів.

Де і коли виникла тригонометрія?

В тригонометрії виділяють три види співідношень:

1) між тригонометричними функціями;

2) між елементами  трикутника ,

3) між елементами сферичного трикутника.

Тригонометрія почалася саме з найбільш складної її частини – сферечної тригонометрії.

Отже, виникла тригонометрія, перш за все, із практичних потреб.

 

 

У древній Греці у другій книзі «Начал»  Евкліда теорема 12 це аналог  теореми  косинусів:

В тупокутних трикутниках квадрат на стороні, що стягує тупий кут, більше (суми) квадратів на сторонах, що містять тупий кут, на двічі взятий прямокутник, поміщений між однією зі сторін при тупому куті, на яку спадає перпендикуляр, і відрізком при тупому куті, який відтинає цей перпендикуляр ззовні.

 

Астроном II століття Клавдій Птолемей в «Альмагесті» доповнив результати Гіппарха. Тринадцять книг «Альмагеста» — найзначніша тригонометрична робота всієї античності. Зокрема, «Амальгест» містить великі п'ятизначні таблиці хорд для гострих і тупих кутів з кроком 30 кутових мінут, що є аналогом таблиць Брадіса.

Терміни «синус» і «косинус» пришли з Індії. Півхорду індійці називали «ардхаджива»(в перекладі з санскриту – «половина тетеви лука»). Це слово переклали «джайб», що арабською мовою означає «випуклість», «пазуха».

А в VІІ столітті «джайб»  переклали на латинь словом «sinus», яке не мало ніякого відношення до пачаткового поняття.  Вийшло все як у грі «зіпсований телефон». Слово косинус є молодшим.Косинус – це скорочення латинського виразу complementy sinus, тобто «додатковий синус» (або «синус додаткової дуги») згадайте cosα=sin(90 - α). Для астрономічних розрахунків був складений ряд тригонометричних таблиць. Перші (чотиризначні) таблиці синусів наведені в стародавній «Сурья-сіддханті» і у Аріабхати (книга «Аріабхатія» V ст.) Таблиці Аріабхати містять 24 значення синусів і синус-верзусів з інтервалом 3°45' (половина кроку таблиць у Гіппарха).

 

На кінець  18 ст. тригонометрія як нука вже склалася.  Тригонометричні функціі знайшли використання у математичному аналізі, фізиці, хімії, техніці – всюди, де доводилося мати справу з періодичними процесами та коливаннями – будь то акустика, оптика чи коливання маятника.

2. Історія тригонометрії середніх віків

У розвиток тригонометрії значний внесок зробили арабські вчені аль – Баттані (IX – X ст.), Абу – ль – Вефа і Насіреддін Тусі (XIIIст.), індійський вчений Бхаскара (XIIст.), а також Регіомонтан, М. Коперник, Т. Браге, Ф. Вієт,  Й.Кеплер. Сучасного вигляду тригонометрія  набула у працях Леонарда  Ейлера.

 

Назва «тангенс»,від латинського tanger (дотикаться), з‘явилося в 1583р.  Tangens перекладається як «дотична» (лінія тангенсів – це дотична до одиничного кола).
Тангенси виникли в зв‘язку з розв‘язком задачі про визначення довжини тіні. Тангенс (а також котангенс, секанс і косеканс) введені в X столітті арабським математиком Абу-ль-Вафою, який склав і перші таблиці для знаходження тангенсів и котангенсів.

 

Важливим відкриттям на початку XVIII століття стало відкриття і широке поширення радіанної міри кутів. Сам термін «радіан» з'явився пізніше, його у 1873 році запропонував англійський інженер Джеймс Томсон.

 

3. Тригонометрія навколо нас

Виникнення тригонометрії пов’язане з потребами астрономії, землемірства та будівничої справи.

 

 

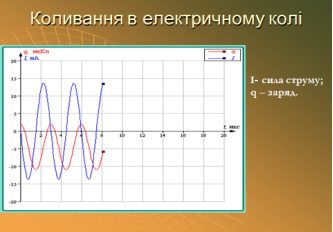
Періодичні зміни фізичної величини в залежності від часу, які відбуваються за законом синуса або косинуса називаються гармонічними коливаннями. Коливання – це фізичні процеси, які точно або приблизно повторюються через однакові інтервали часу. Залежно від фізичної природи їх поділяють на механічні та електромагнітні.

 

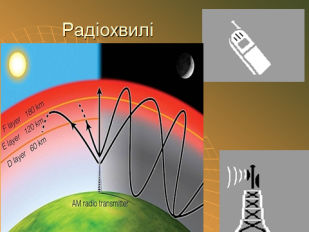
Як і коливання, хвилі за своєю природою поділяються на механічні та електромагнітні. Механічна хвиля – це процес поширення механічних коливань у пружному середовищі. Прикладом найпоширеніших механічних хвиль є звук, хвилі на поверхні рідини. Джерело хвиля – це коливальна система яка під час коливань передає частину своєї енергії в навколишнє середовище.

 

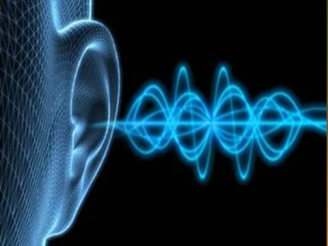
Що ж таке звук? Якщо струну натягнути, а потім відпустити, то вони почне коливатися, як гойдалка чи маятник годинника. А оскільки це коливання відбувається у повітрі, то струна змушує коливатися повітря, що розташоване поруч з нею.

Людське вухо сприймає далеко не всі коливання. Ми чуємо звуки, які створюють тіла, як здійснюють від 16 до 20000 коливань за секунду. Так коливання називають акустичними. Розділ фізики, який вивчає такі звуки називають акустикою.

 

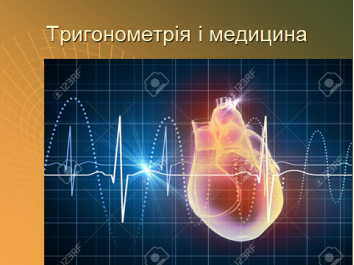
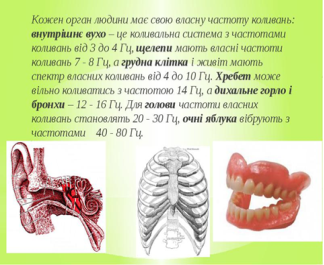
Тригонометрія і медицина

 

Тригонометрія у природі