Презентація "Бінарний пошук"
Про матеріал
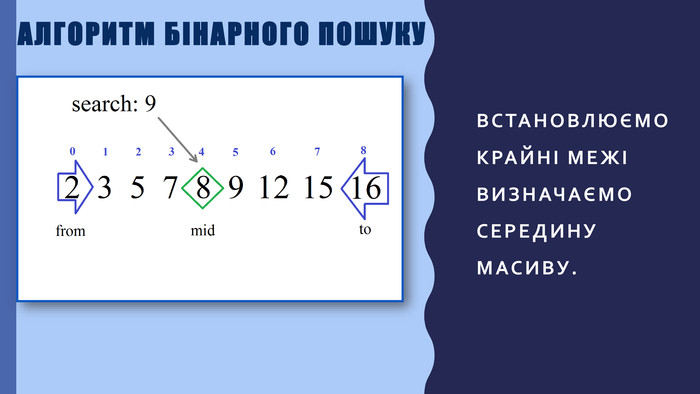
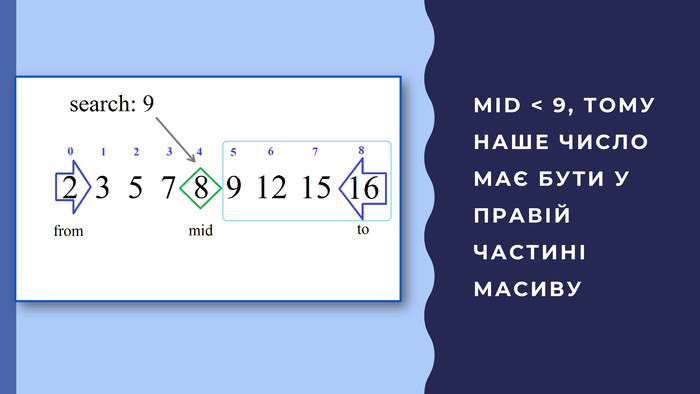
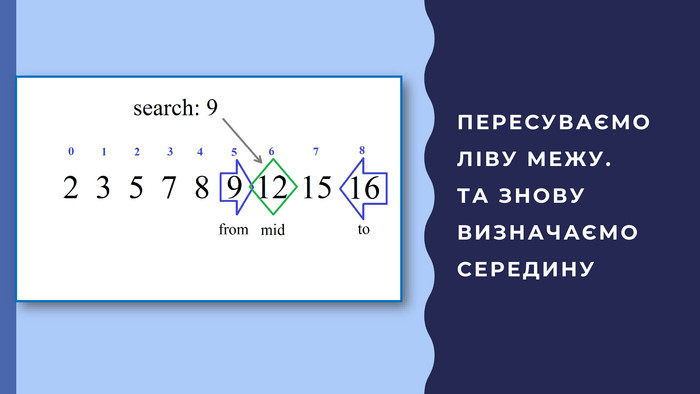
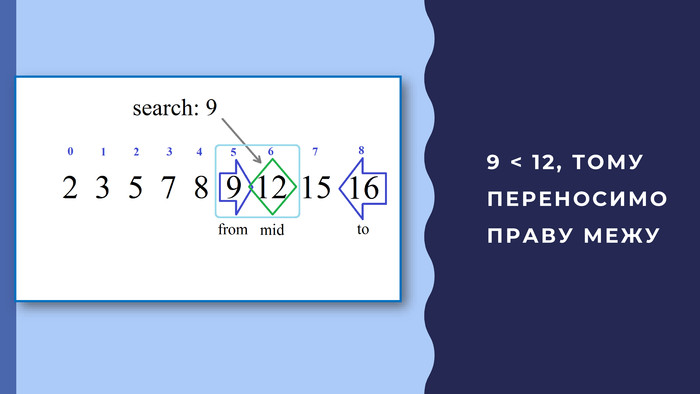
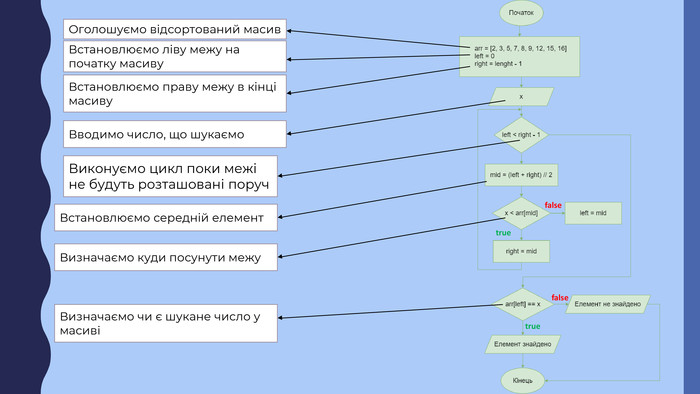
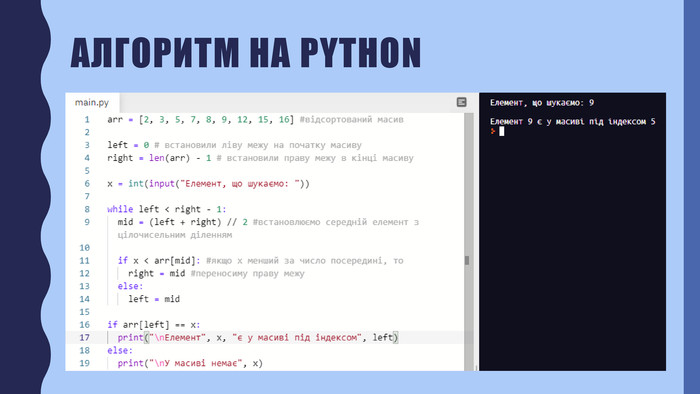
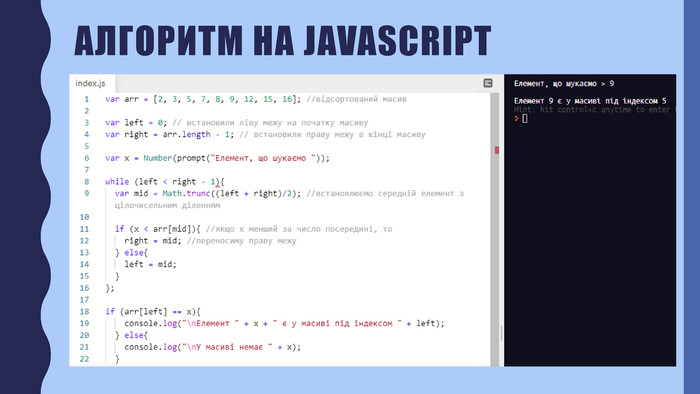
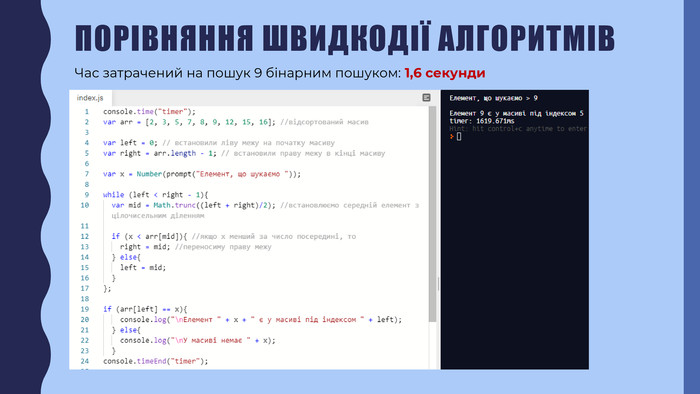
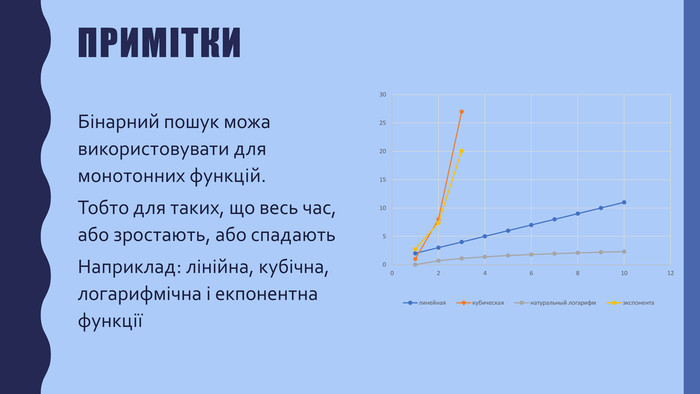
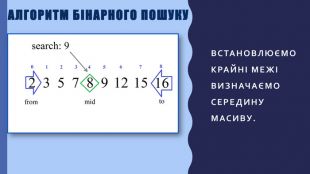
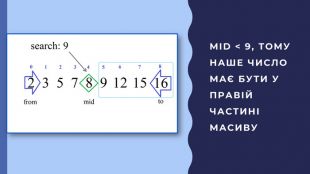
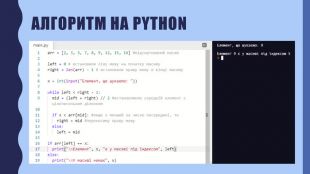
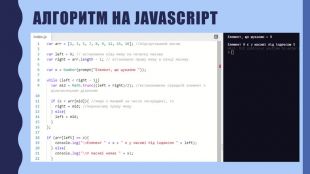
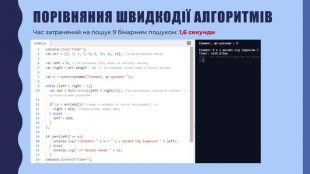
В презентації описана реалізація бінарного пошуку в мовах програмування javascript та python Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку