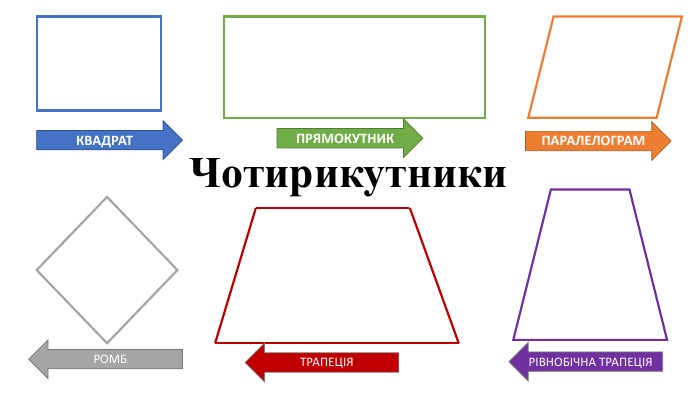
Презентація "Чотирикутники"
Про матеріал
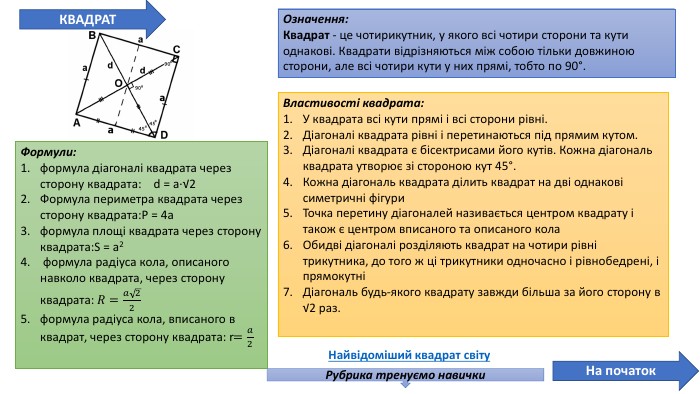
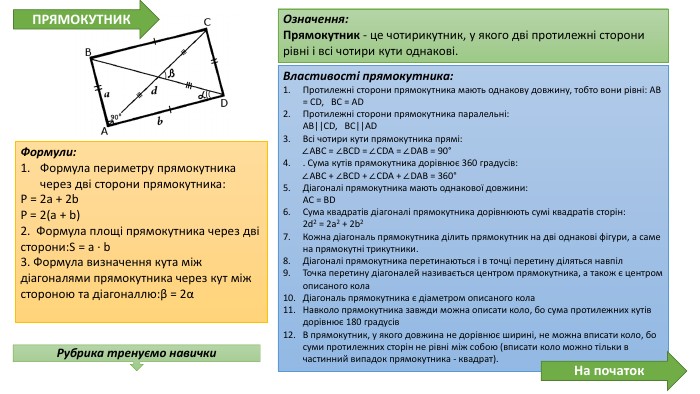
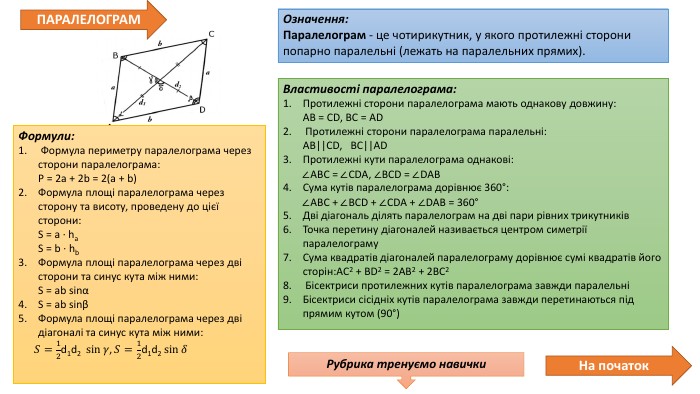
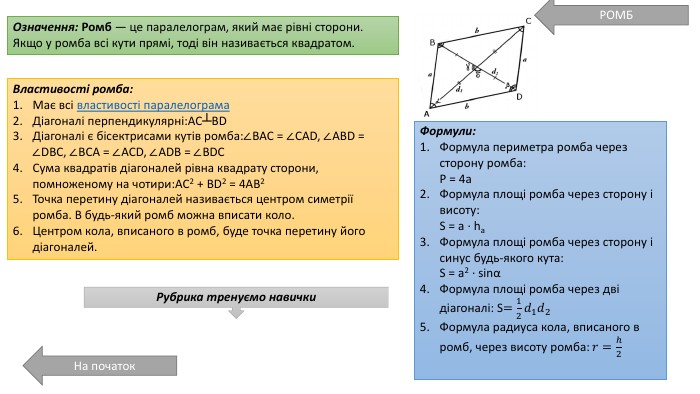
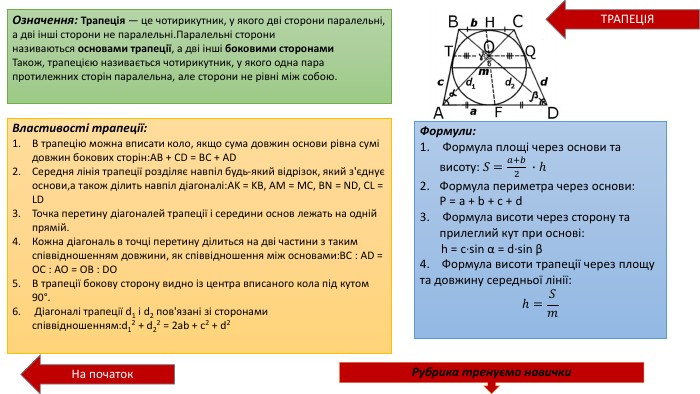
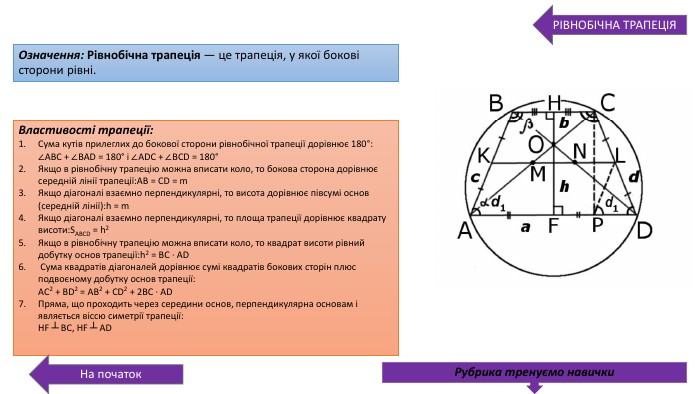
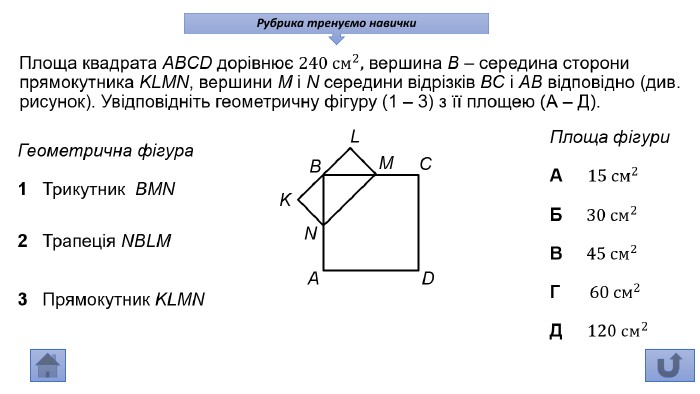
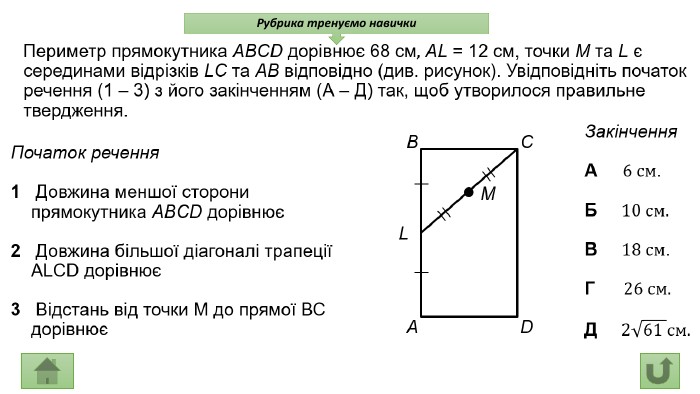
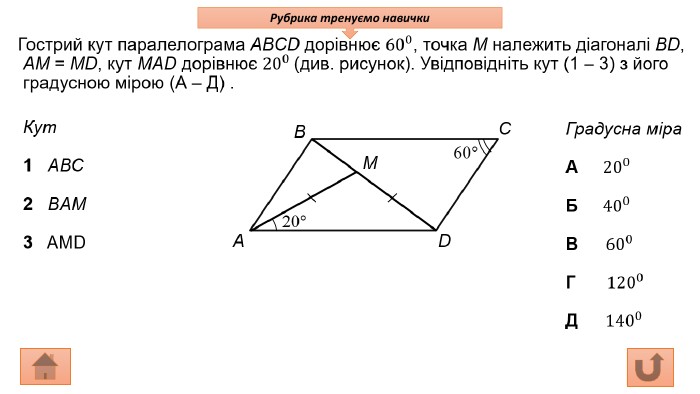
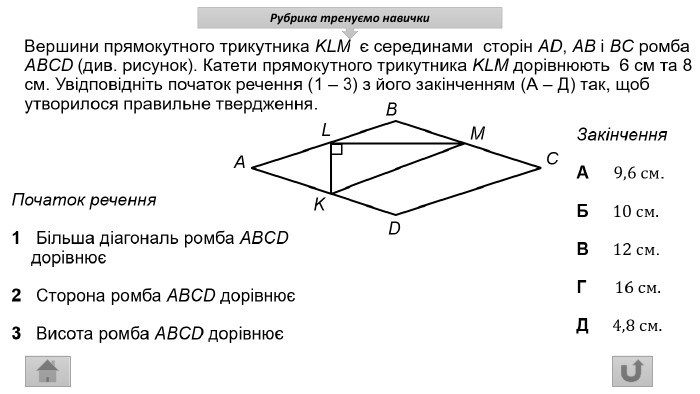
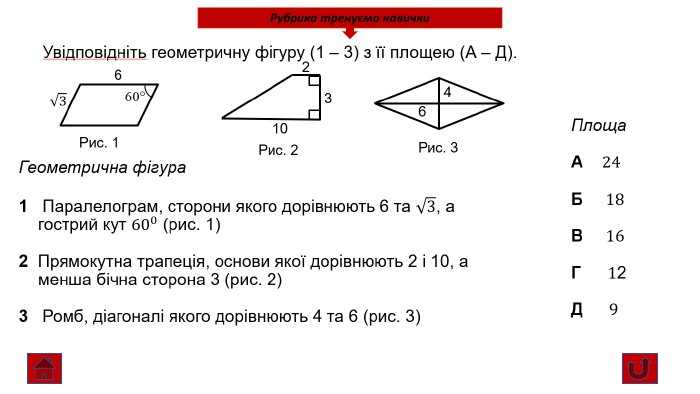
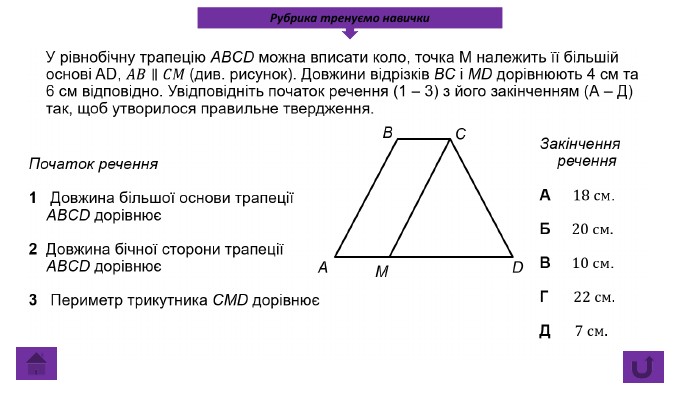
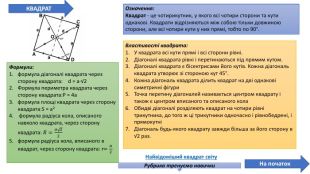
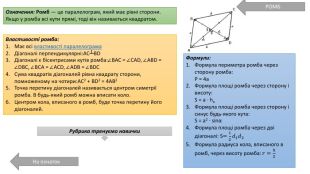
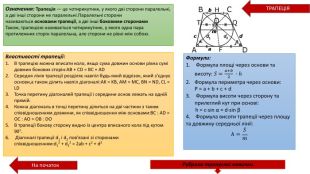
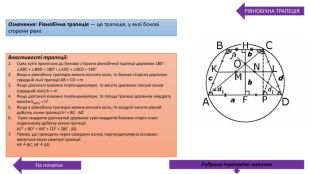
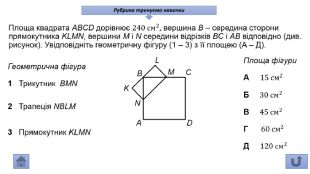
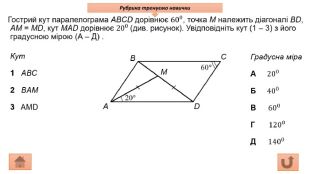
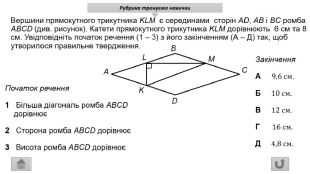
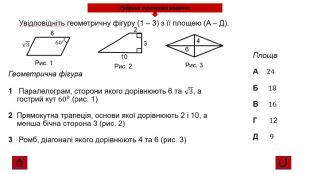
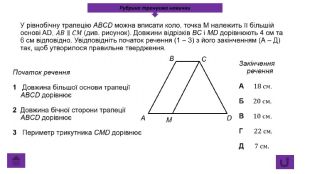
Презентація про всі види опуклих чотирикутників які вивчаються у 8 класі. У даній презентації ви можете знайти властивості, означення та задачі до даної теми. Можна використовувати під час проведення уроку узагальнення у 8 класі. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку