Презентація для уроку-узагальнення з теми: «Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики»

Прикладна математика. Розбір задач із теми:«Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики»ЗНО 2017-2021 років. Вчитель математики. Куп’янського ліцею №1 Куп’янської міської ради Харківської областіКириловець Світлана Петрівнаrrrrrr

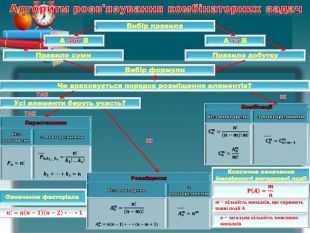
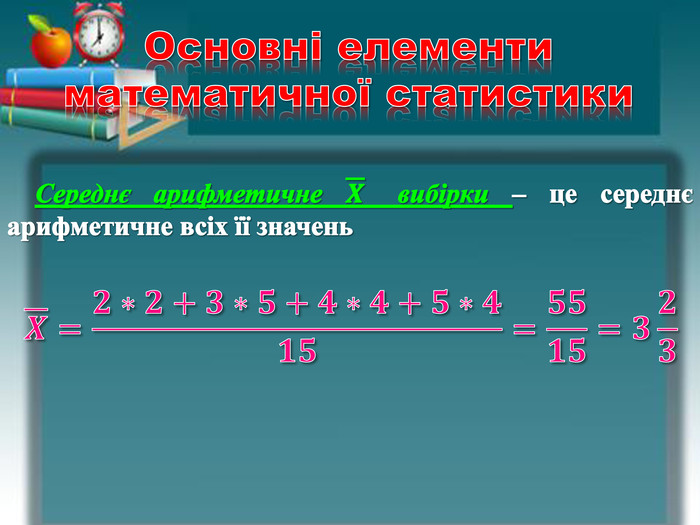
Алгоритм розв'язування комбінаторних задач. Вибір правила. Вибір формули. Чи враховується порядок розміщення елементів?А або ВА та ВПравило суми. Правило добутку. Усі елементи беруть участь?{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Перестановкибез повтореньз повтореннями𝑷𝒏=𝐧!𝑷𝐧,  𝒌𝟏,…,𝒌𝒔=𝐧!𝒌𝟏!…𝒌𝒔!𝒌𝟏+…+𝒌𝒔=𝐧{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Перестановкибез повтореньз повтореннями{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Комбінаціїбез повтореньз повтореннями𝐂𝐧𝐦=𝐧!(𝐧−𝐦)!𝐦! 𝐂𝐧𝐦=𝐀𝐧𝐦𝐦! 𝐂𝐧𝐦=𝐂𝐧+𝐦−𝟏𝐦 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Комбінаціїбез повтореньз повтореннями𝒏!=𝒏𝒏−𝟏𝒏−𝟐∗…∗𝟏 ТАКТАКНІНІ𝐏𝑨=𝒎𝒏 m − кількість випадків, що сприяють появі події А n − загальна кількість можливих випадків Класичне означення ймовірності випадкової подіїОзначення факторіала{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Розміщеннябез повтореньз повтореннями𝑨𝒏𝒎=𝐧!(𝐧−𝐦)!𝑨𝒏𝒎=𝐧𝐧−𝟏∗…∗(𝐧−𝐦+𝟏)𝑨𝒏𝒎=𝒏𝒎{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Розміщеннябез повтореньз повтореннямиrrrr

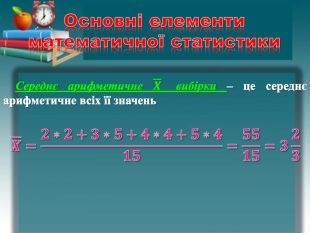
Основні елементи математичної статистики. Генеральна сукупність – сукупність усіх об’єктів, що підлягають дослідженню. Вибіркою називають сукупність об’єктів, вибраних навмання з генеральної сукупності2, 5, 4, 3, 3, 2, 4, 4, 5, 3, 5, 3, 4, 3, 5 Ранжування вибірки – розташування випадкових величин вибірки за принципом неспадання, тобто кожне наступне число вибірки не менше за попереднє2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Елементи2345 Кількість елементів2544 Розмах вибірки R – це різниця між найбільшим і найменшим значеннями у вибірці R=5-2=3 Мода вибірки Мо – це значення, яке трапляється у вибірці найчастіше Мо=3 Медіана вибірки Ме – це серединне значення ранжованої вибірки2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5 Ме=4 Якщо у вибірці парна кількість чисел, то медіана є середнім арифметичним двох чисел, що стоять посередині 1, 2, 2, 2, 3, 3, 4, 5 Ме=(2+3)/2=2,5rrrr

Основні елементи математичної статистики. Середнє арифметичне 𝑿 вибірки – це середнє арифметичне всіх її значень 𝑿=𝟐∗𝟐+𝟑∗𝟓+𝟒∗𝟒+𝟓∗𝟒𝟏𝟓=𝟓𝟓𝟏𝟓=𝟑𝟐𝟑 rrrr

4. На діаграмі відображено дані про обсяг виробництва какао-бобів (у тис. тонн) у 2009 році в семи країнах-лідерах. ПРОБНЕ ЗНО 2017І місце – Кот д’ІвуарІІ місце – ІндонезіяІІІ місце – Гана. Користуючись діаграмою, укажіть проміжок, якому належить значення маси (у тис. тонн) какао-бобів, вирощених у країні, що посіла у 2009 році третє місце за обсягом їх виробництва.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД[200; 300][300; 400][600; 700][700; 800][1200; 1300]3від 600 до 700 тис. тонн21rrrr

29. Музей має надати чотири картини відомого художника для виставки, присвяченої дню його народження. Одну картину вибирають з діючої експозиції музею, що містить 5 робіт цього художника, а три інші – з архіву, у якому є 10 його картин. Скільки всього способів такого вибору?ПРОБНЕ ЗНО 2017 Діюча експозиція. Архів. Загальна кількість картин5 робіт10 картиніМаємо обрати1 роботу3 картиниіВикористовуємо правило добутку. С𝟓𝟏 С𝟏𝟎𝟑 *𝐂𝐧𝐦=𝐧!(𝐧−𝐦)!𝐦! 𝒏!=𝒏𝒏−𝟏𝒏−𝟐∗…∗𝟏 С𝟓𝟏∗С𝟏𝟎𝟑=𝟓!𝟓−𝟏!∙𝟏!∗𝟏𝟎!𝟏𝟎−𝟑!∙𝟑!=𝟓∙𝟒!𝟒!∙𝟏!∗𝟏𝟎∙𝟗∙𝟖∙𝟕!𝟕!∙𝟑!=𝟓∙𝟏𝟎∙𝟗∙𝟖𝟏∙𝟐∙𝟑=𝟓∙𝟓∙𝟑∙𝟖=𝟔𝟎𝟎 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Відповідь600,   53rrrr

4. У таблиці наведено дані про кількість глядачів, які відвідали кінотеатр протягом п’яти днів тижня. ЗНО 2017{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}День тижня. Пн. Вт. Ср. Чт. Пт. Кількість відвідувачів82116102140130 На діаграмах немає шкали (градації) кількості глядачів. Визначте, на якій діаграмі правильно відображено дані, наведені в таблиці. Найменше значення - 82 Найбільше значення - 140 П’ятниця знаходиться на ІІ місці після четверга - 130 Порівнюємо інші дні тижня. Вівторок – 116, середа - 102rrrr

29. У торбинці лежать 3 цукерки з молочного шоколаду та m цукерок з чорного шоколаду. Усі цукерки – однакової форми й розміру. Якого найменшого значення може набувати m, якщо ймовірність навмання витягнути з торбинки цукерку з молочного шоколаду менша за 0,25?ЗНО 2017𝐏𝑨=𝒎𝒏 m − кількість випадків, що сприяють появі події А n − загальна кількість можливих випадків Класичне `означення ймовірності випадкової подіїМаємо3 цукерки з молочного шоколадуm цукерок із чорногота. Загальна кількістьn= m+3 Кількість, що сприяє подіїm=3{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Відповідь10,   𝑷(𝑨)=𝟑𝒎+𝟑 𝑷𝑨<𝟎,𝟐𝟓 𝟑𝒎+𝟑<𝟎,𝟐𝟓 𝟑𝒎+𝟑<𝟏𝟒 𝒎+𝟑>𝟎 ∗𝒎+𝟑𝟒 4*3 <𝒎+𝟑 𝟏𝟐<𝒎+𝟑 12 - 3 <𝒎 9 <𝒎 𝒎>𝟗 𝒎 𝝐 (𝟗; +∞) Найменша кількість цукерок - 10rrrrrrrrrrrr

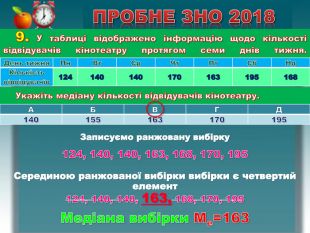
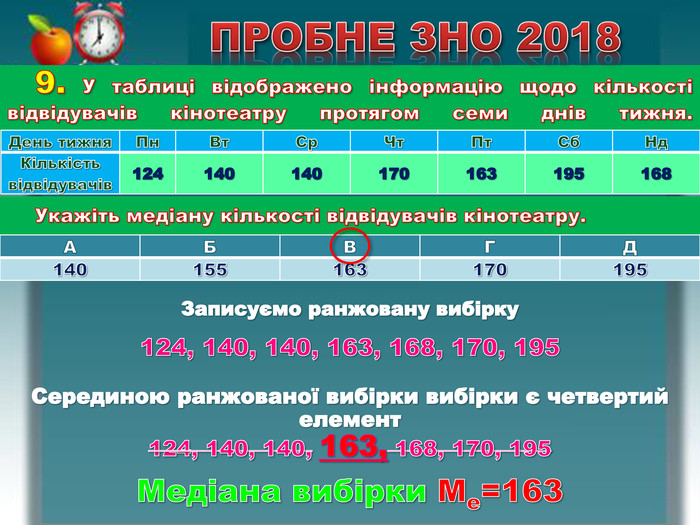
9. У таблиці відображено інформацію щодо кількості відвідувачів кінотеатру протягом семи днів тижня.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}День тижня. Пн. Вт. Ср. Чт. Пт. Сб. Нд. Кількість відвідувачів124140140170163195168 ПРОБНЕ ЗНО 2018 Укажіть медіану кількості відвідувачів кінотеатру.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД140155163170195 Записуємо ранжовану вибірку124, 140, 140, 163, 168, 170, 195 Серединою ранжованої вибірки вибірки є четвертий елемент 124, 140, 140, 163, 168, 170, 195 Медіана вибірки Me=163rrrr

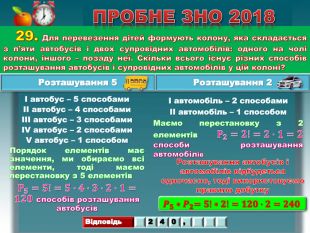
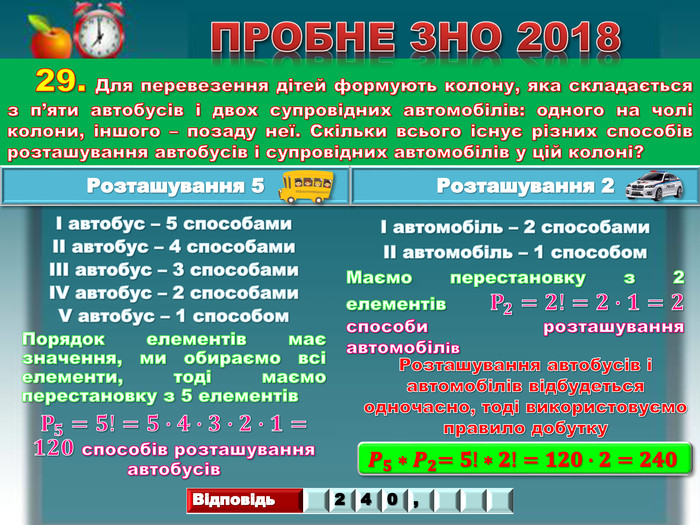
29. Для перевезення дітей формують колону, яка складається з п’яти автобусів і двох супровідних автомобілів: одного на чолі колони, іншого – позаду неї. Скільки всього існує різних способів розташування автобусів і супровідних автомобілів у цій колоні?ПРОБНЕ ЗНО 2018І автобус – 5 способамиІІ автобус – 4 способамиІІІ автобус – 3 способами. IV автобус – 2 способами. V автобус – 1 способом. Порядок елементів має значення, ми обираємо всі елементи, тоді маємо перестановку з 5 елементів𝐏𝟓=𝟓!=𝟓∙𝟒∙𝟑∙𝟐∙𝟏=𝟏𝟐𝟎 способів розташування автобусів І автомобіль – 2 способамиІІ автомобіль – 1 способом. Маємо перестановку з 2 елементів𝐏𝟐=𝟐!=𝟐∙𝟏=𝟐 способи розташування автомобілів Розташування 5 Розташування 2 𝑷𝟓∗𝑷𝟐=𝟓!∗𝟐!=𝟏𝟐𝟎∙𝟐=𝟐𝟒𝟎 Розташування автобусів і автомобілів відбудеться одночасно, тоді використовуємо правило добутку{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Відповідь240,   rrrr

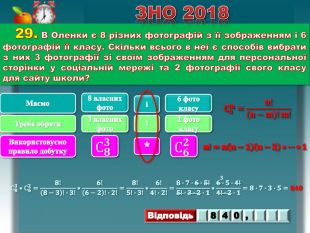
12. Учень з понеділка до п’ятниці записував час (у хвилинах), який він витрачав на дорогу до школи та зі школи (див. таблицю). ЗНО 2018 На скільки хвилин у середньому дорога зі школи триваліша за дорогу до школи?{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД23456 До школи. Зі школи𝑿𝟏=𝟏𝟗+𝟐𝟎+𝟐𝟏+𝟏𝟕+𝟐𝟑𝟓=𝟏𝟎𝟎𝟓=𝟐𝟎 (хв) Порівнюємо отримані значення𝑿𝟐=𝟐𝟖+𝟐𝟐+𝟐𝟎+𝟐𝟓+𝟑𝟎𝟓=𝟏𝟐𝟓𝟓=𝟐𝟓 (хв) 𝟐𝟓 хв−𝟐𝟎 хв=𝟓 (хв) rrrr

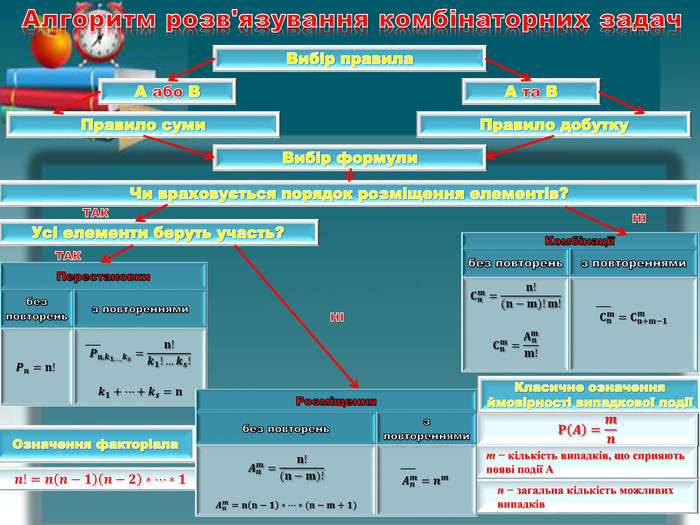
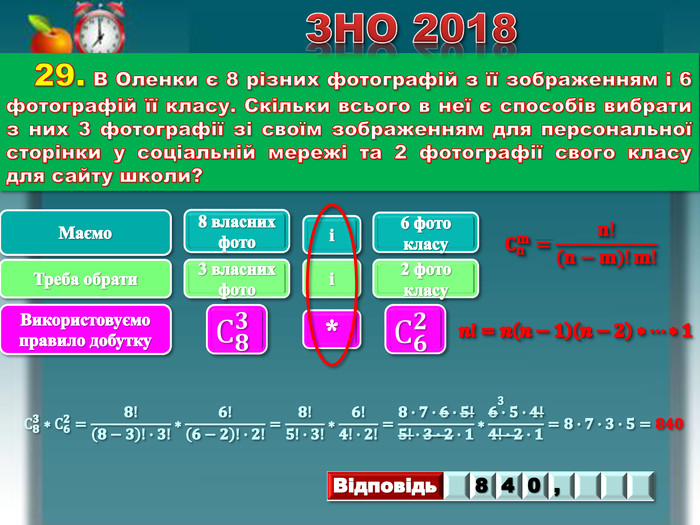
29. В Оленки є 8 різних фотографій з її зображенням і 6 фотографій її класу. Скільки всього в неї є способів вибрати з них 3 фотографії зі своїм зображенням для персональної сторінки у соціальній мережі та 2 фотографії свого класу для сайту школи?ЗНО 2018 Маємо8 власних фото6 фото класуіТреба обрати3 власних фото2 фото класуіВикористовуємо правило добутку. С𝟖𝟑 С𝟔𝟐 *𝐂𝐧𝐦=𝐧!(𝐧−𝐦)!𝐦! 𝒏!=𝒏𝒏−𝟏𝒏−𝟐∗…∗𝟏 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Відповідь840,   С𝟖𝟑∗С𝟔𝟐=𝟖!𝟖−𝟑!∙𝟑!∗𝟔!𝟔−𝟐!∙𝟐!=𝟖!𝟓!∙𝟑!∗𝟔!𝟒!∙𝟐!=𝟖∙𝟕∙𝟔∙𝟓!𝟓!∙𝟑∙𝟐∙𝟏∗𝟔∙𝟓∙𝟒!𝟒!∙𝟐∙𝟏=𝟖∙𝟕∙𝟑∙𝟓=𝟖𝟒𝟎 3rrrr

29. Для оформлення салону краси вирішили замовити в магазині квітів 2 орхідеї різних кольорів та 5 кущів хризантем п’яти різних кольорів. Усього в магазині є в продажу орхідеї 10 кольорів та кущі хризантем 8 кольорів. Скільки всього є способів формування такого замовлення?ПРОБНЕ ЗНО 2019 Маємо10 кольорів орхідей8 кольорів хризантемта. Треба обрати2 кольори орхідеї5 кольорів хризантем. С𝟖𝟓 та. Використовуємо правило добутку. С𝟏𝟎𝟐 *{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Відповідь2520,   4 С𝟏𝟎𝟐∗С𝟖𝟓=𝟏𝟎!𝟏𝟎−𝟐!∙𝟐!∗𝟖!𝟖−𝟓!∙𝟓!=𝟏𝟎!𝟖!∙𝟐!∙𝟖!𝟑!∙𝟓!=𝟏𝟎∙𝟗∙𝟖∙𝟕∙𝟔∙𝟓!𝟏∙𝟐∙𝟔∙𝟓!=𝟏𝟎∙𝟗∙𝟕∙𝟒=𝟐𝟓𝟐𝟎 rrrr

11. На діаграмі відображено розподіл кількості працівників фірми за віком. Скільки всього працівників працює на цій фірмі?ЗНО 201929. У фінал пісенного конкурсу вийшло 4 солісти та 3 гурти. Порядковий номер виступу фіналістів визначають жеребкуванням. Скільки всього є варіантів послідовностей виступів фіналістів, якщо спочатку виступатимуть гурти, а після них — солісти?Уважайте, що кожен фіналіст виступатиме у фіналі лише один раз. Виконай самостійно{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД4096120144110rrrrrrrr

11. На вершину гори ведуть 5 доріг. Скільки всього є варіантів вибору маршруту підйому на вершину гори однією дорогою, а спуску - іншою?ЗНО 202031. Для участі в роботі студентської ради з кожної з двох груп навмання вибирають по 1 студенту. Серед 24 студентів першої групи проживають у гуртожитку 6 студентів, а серед 28 студентів другої групи – 14 студентів. Яка ймовірність того, що обидва вибрані для роботи в раді студенти будуть з тих, хто проживає в гуртожитку?Виконай самостійно{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД59102025rrrrrrrr

25. У першому класі 15 дівчаток, з яких лише одна на ім‘я Дарина, і 11 хлопчиків. На першому уроці вчителька навмання формує пари дітей, які сидітимуть за однією партою. Першою вона вибирає пару для Дарини. Яка ймовірність того, що Дарина сидітиме за однією партою з дівчинкою?ЗНО 202129. Редактор стрічки новин вирішує, у якій послідовності розмістити 6 різних новин: 2 політичні, 3 суспільні й 1 спортивну. Скільки всього є різних послідовностей розміщення цих 6 новин у стрічці за умови, що політичні новини мають передувати іншим, а спортивна – бути останньою? Вважайте, що кожну із цих 6 новин у стрічці не повторюють. Виконай самостійноrrrrrrrr

Успішногонавчання!