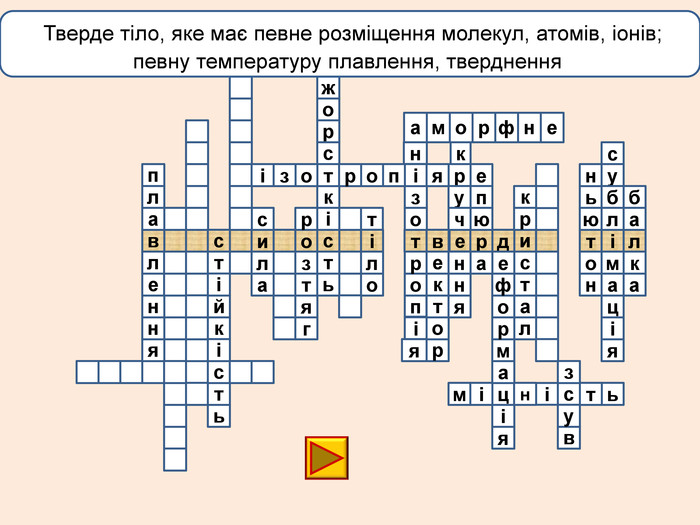
Презентація до бінарного заняття-флешмоб "Властивості твердих тіл"
Презентація до бінарного заняття (флешмоб) з дисципліни «Технічна механіка» та предмету «Фізика» за темою "Властивості твердих тіл"



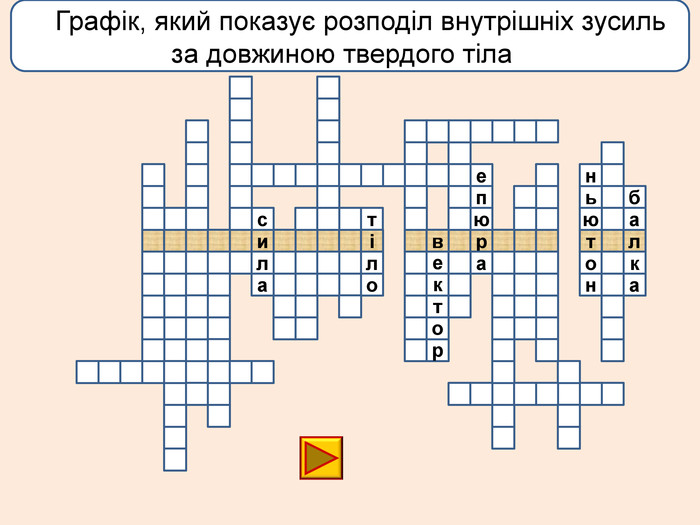
































![Метод допустимих напружень. Допустимим напруженням [σ] називається найбільше напруження, при якому забезпечується міцність і довговічність проєктованого елемента конструкції. Граничними називають стани, при яких конструкція, будівля або споруда перестає задовольняти заданим вимогам в процесі зведення або експлуатації. Метод допустимих напружень. Допустимим напруженням [σ] називається найбільше напруження, при якому забезпечується міцність і довговічність проєктованого елемента конструкції. Граничними називають стани, при яких конструкція, будівля або споруда перестає задовольняти заданим вимогам в процесі зведення або експлуатації.](/uploads/files/622807/260938/282616_images/87.jpg)

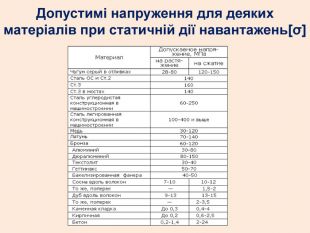
![Допустимі напруження для деяких матеріалів при статичній дії навантажень[σ] Допустимі напруження для деяких матеріалів при статичній дії навантажень[σ]](/uploads/files/622807/260938/282616_images/89.jpg)

![1. Перевірочний (перевірка на міцність)При заданих значеннях поздовжньої сили і площі поперечного перерізу визначають робоче (розрахункове) напруження і порівнюють його з допустимим напруженням:σ = N/S≤[σ] Значення допустимих напружень для деяких матеріалів при статичній дії навантажень приведені в таблиці (Додаток). Потім обчислюють розбіжність (у відсотках) між фактичним і допустимим значеннями робочого напруження. Якщо перенапруження перевищує 5%, міцність конструкції, яка розраховується, вважається недостатньою. Розрахунки на міцність виконуються в кілька етапів:а) при необхідності визначаються опорні реакції;б) розраховуються внутрішні силові фактори і будуються їх епюри;в) визначаються найбільш навантажені ділянки або перетини бруса;г) залежно від умови задачі виконується необхідний розрахунок. 1. Перевірочний (перевірка на міцність)При заданих значеннях поздовжньої сили і площі поперечного перерізу визначають робоче (розрахункове) напруження і порівнюють його з допустимим напруженням:σ = N/S≤[σ] Значення допустимих напружень для деяких матеріалів при статичній дії навантажень приведені в таблиці (Додаток). Потім обчислюють розбіжність (у відсотках) між фактичним і допустимим значеннями робочого напруження. Якщо перенапруження перевищує 5%, міцність конструкції, яка розраховується, вважається недостатньою. Розрахунки на міцність виконуються в кілька етапів:а) при необхідності визначаються опорні реакції;б) розраховуються внутрішні силові фактори і будуються їх епюри;в) визначаються найбільш навантажені ділянки або перетини бруса;г) залежно від умови задачі виконується необхідний розрахунок.](/uploads/files/622807/260938/282616_images/92.jpg)
![2. Проєктувальний розрахунок (підбір розмірів перетинів)Навантаження і матеріал (допустимі напруження) при цьому розрахунку відомі. Необхідно визначити площу поперечного перерізу, при якій буде забезпечена міцність елемента, який розраховується. S≥ N/[σ] 2. Проєктувальний розрахунок (підбір розмірів перетинів)Навантаження і матеріал (допустимі напруження) при цьому розрахунку відомі. Необхідно визначити площу поперечного перерізу, при якій буде забезпечена міцність елемента, який розраховується. S≥ N/[σ]](/uploads/files/622807/260938/282616_images/93.jpg)
![3. Визначення допустимого навантаження. За відомими розмірами перетину даного елемента конструкції і механічними характеристиками його матеріалу потрібно встановити найбільше навантаження, безпечне для цього елемента,[N]≤S[σ] 3. Визначення допустимого навантаження. За відомими розмірами перетину даного елемента конструкції і механічними характеристиками його матеріалу потрібно встановити найбільше навантаження, безпечне для цього елемента,[N]≤S[σ]](/uploads/files/622807/260938/282616_images/94.jpg)
![Зведемо в таблицю{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Вид розрахунку Метод допустимих напружень. Метод граничних станів. Перевірочний σ = N/S≤[σ]σ = Nрозр. ∕ S≤RПроєктувальний S≥ N/[σ]S≥Nрозр. ∕ [R]Визначення допустимого навантаження[N]≤S[σ]Nрозр. ≤S∙R Зведемо в таблицю{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Вид розрахунку Метод допустимих напружень. Метод граничних станів. Перевірочний σ = N/S≤[σ]σ = Nрозр. ∕ S≤RПроєктувальний S≥ N/[σ]S≥Nрозр. ∕ [R]Визначення допустимого навантаження[N]≤S[σ]Nрозр. ≤S∙R](/uploads/files/622807/260938/282616_images/96.jpg)
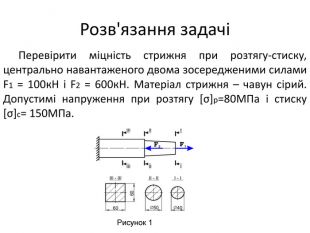
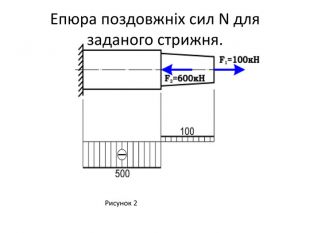
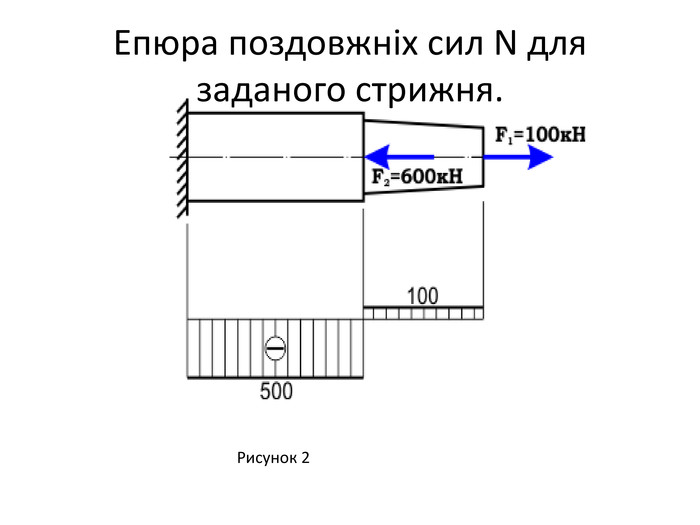
![Розв'язання задачіПеревірити міцність стрижня при розтягу-стиску, центрально навантаженого двома зосередженими силами F1 = 100к. Н і F2 = 600к. Н. Матеріал стрижня – чавун сірий. Допустимі напруження при розтягу [σ]p=80 МПа і стиску [σ]c= 150 МПа. Рисунок 1 Розв'язання задачіПеревірити міцність стрижня при розтягу-стиску, центрально навантаженого двома зосередженими силами F1 = 100к. Н і F2 = 600к. Н. Матеріал стрижня – чавун сірий. Допустимі напруження при розтягу [σ]p=80 МПа і стиску [σ]c= 150 МПа. Рисунок 1](/uploads/files/622807/260938/282616_images/97.jpg)
![Розв'язання задачіДля правої частини стрижня небезпечним є перетин І-І, в якому діє поздовжня сила розтягу. Nр=100к. Н, а площа перерізу А1=42∙π/4=12,56см².σ = Nр/А1=100∙10³/12,56∙10¯⁴=79,6∙10⁶Н/м²=79,6 МПа<[σ]р=80 МПа. У лівій стислій частині стрижня поздовжня сила за абсолютною величиною дорівнює Nс=500к. Н і всі перетини небезпечні. А2 = 62 = 36 см2.σ = Nс/А2=500∙10³/36∙10¯⁴=138,9∙10⁶Н/м²=138,9 МПа<[σ]с=150 МПа Розв'язання задачіДля правої частини стрижня небезпечним є перетин І-І, в якому діє поздовжня сила розтягу. Nр=100к. Н, а площа перерізу А1=42∙π/4=12,56см².σ = Nр/А1=100∙10³/12,56∙10¯⁴=79,6∙10⁶Н/м²=79,6 МПа<[σ]р=80 МПа. У лівій стислій частині стрижня поздовжня сила за абсолютною величиною дорівнює Nс=500к. Н і всі перетини небезпечні. А2 = 62 = 36 см2.σ = Nс/А2=500∙10³/36∙10¯⁴=138,9∙10⁶Н/м²=138,9 МПа<[σ]с=150 МПа](/uploads/files/622807/260938/282616_images/99.jpg)


![Задача для самостійного розв'язання2. Визначаємо напруження в поперечних перетинах штанги. Перетин. I-Iσ1 = N1/S=80∙10³/20∙20=80000/400=200 Н/мм²Перетин. II-IIσ2 = N2/S=100∙10³/20∙20=100000/400=250 Н/мм²Будуємо епюри поздовжніх сил та напружень (рисунок 6). Небезпечним є перетин верхньої ділянки, в її межах виникає найбільше робоче напруження. Штанга виготовлена з вуглецевої конструкційної сталі. Допустиме напруження для цього матеріалу:[σр] = 59-245 Н/мм2σ2=250 Н/мм2> [σр] = 59-245 Н/мм2 Зіставляючи напруження в межах ділянки II-II з допустимим, виявляємо, що має місце перенапруження.250-245/245∙100%=0,02=2%Таке незначне перенапруження ( не вище 5%) може бути допущено. Висновок: міцність штанги забезпечена. Рисунок 6 Задача для самостійного розв'язання2. Визначаємо напруження в поперечних перетинах штанги. Перетин. I-Iσ1 = N1/S=80∙10³/20∙20=80000/400=200 Н/мм²Перетин. II-IIσ2 = N2/S=100∙10³/20∙20=100000/400=250 Н/мм²Будуємо епюри поздовжніх сил та напружень (рисунок 6). Небезпечним є перетин верхньої ділянки, в її межах виникає найбільше робоче напруження. Штанга виготовлена з вуглецевої конструкційної сталі. Допустиме напруження для цього матеріалу:[σр] = 59-245 Н/мм2σ2=250 Н/мм2> [σр] = 59-245 Н/мм2 Зіставляючи напруження в межах ділянки II-II з допустимим, виявляємо, що має місце перенапруження.250-245/245∙100%=0,02=2%Таке незначне перенапруження ( не вище 5%) може бути допущено. Висновок: міцність штанги забезпечена. Рисунок 6](/uploads/files/622807/260938/282616_images/102.jpg)











![Домашнє завдання: Викладач фізики:вивчити конспект (§13.1-13.8, 14.1-14.8);Викладач технічної механіки: вивчити конспект ( с. 162-170 [2]) Домашнє завдання: Викладач фізики:вивчити конспект (§13.1-13.8, 14.1-14.8);Викладач технічної механіки: вивчити конспект ( с. 162-170 [2])](/uploads/files/622807/260938/282616_images/114.jpg)

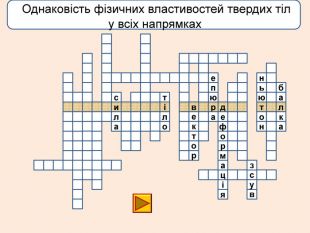
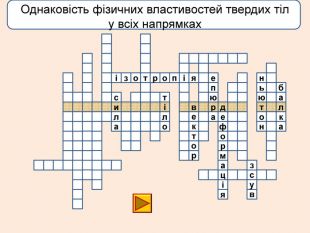
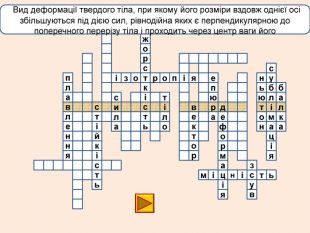
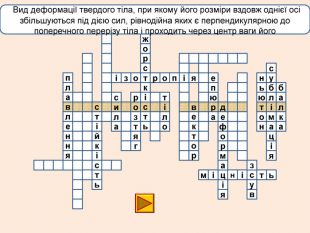
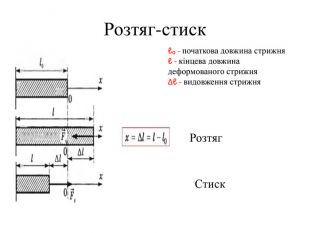
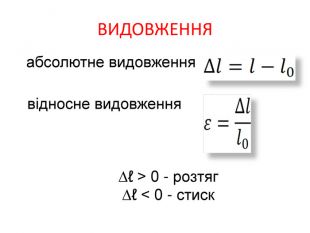
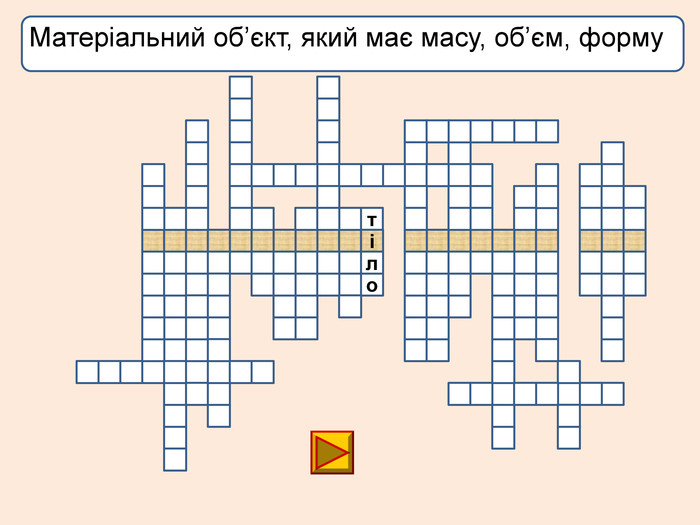
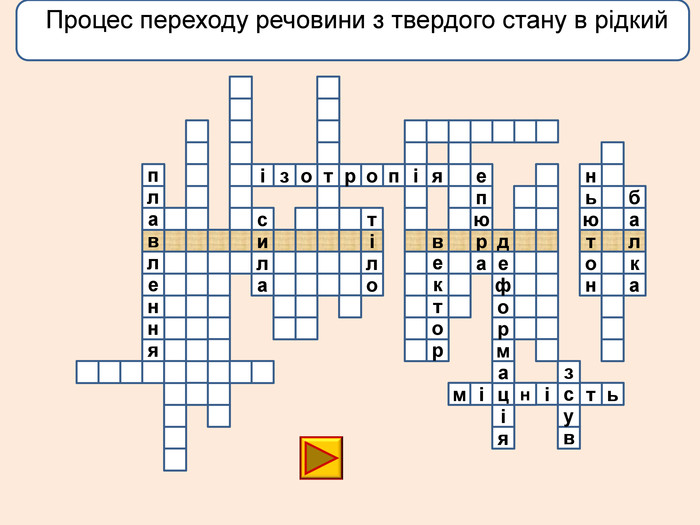
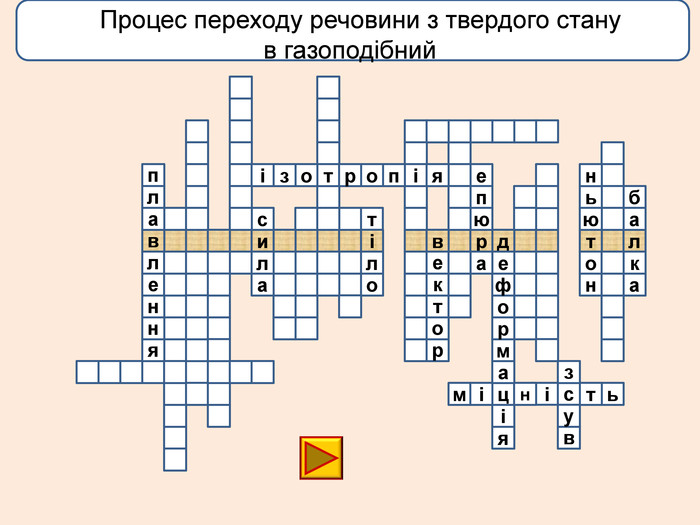
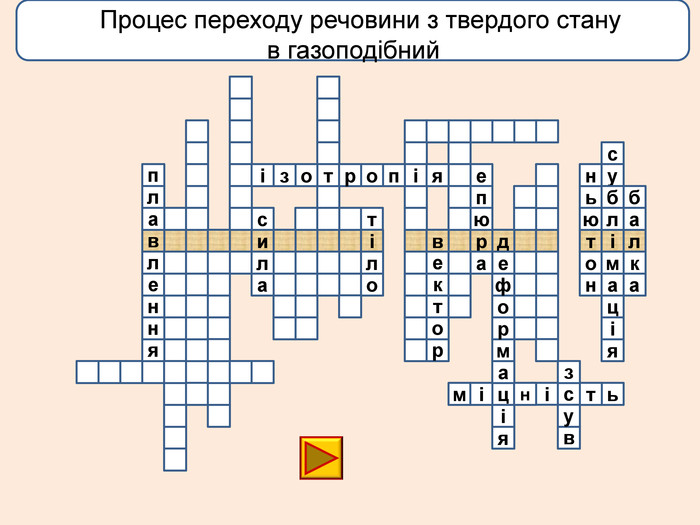
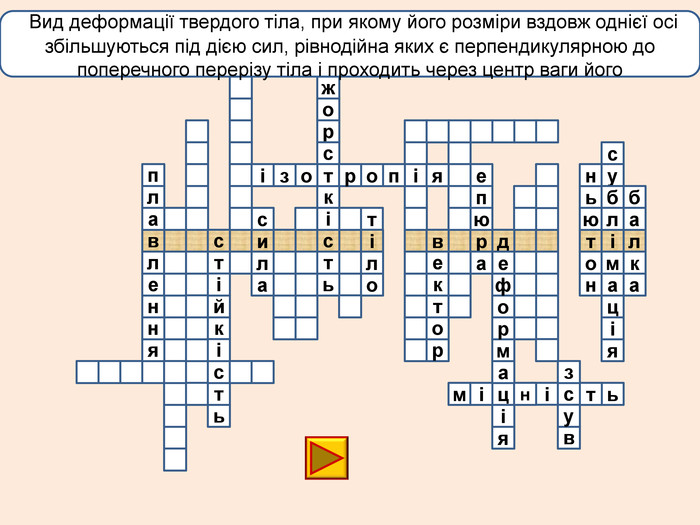
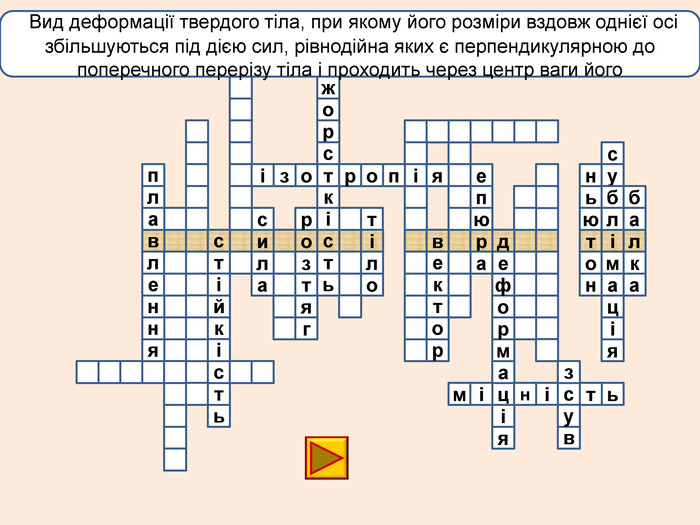
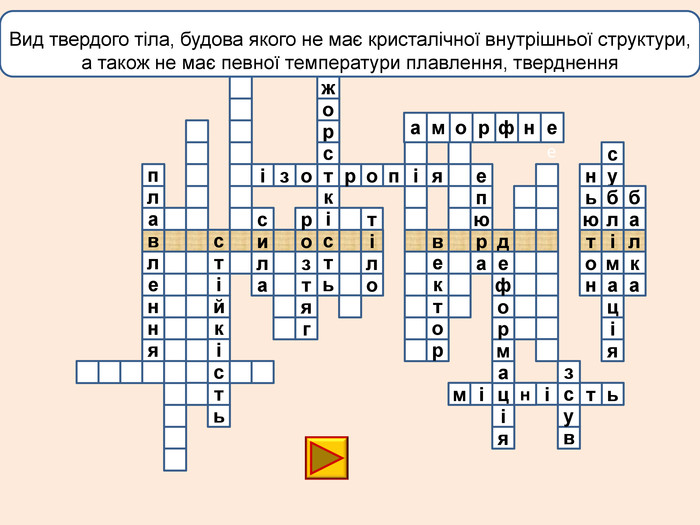
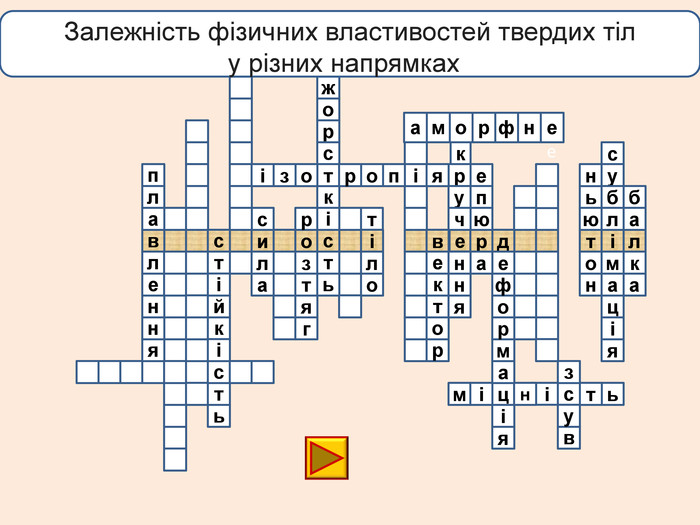
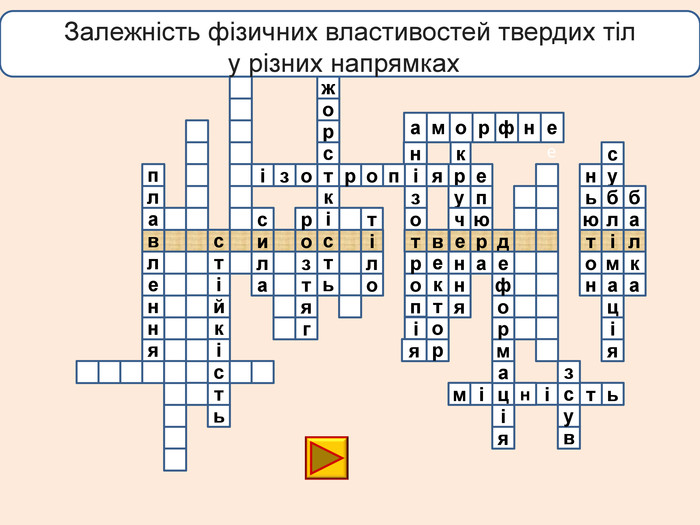
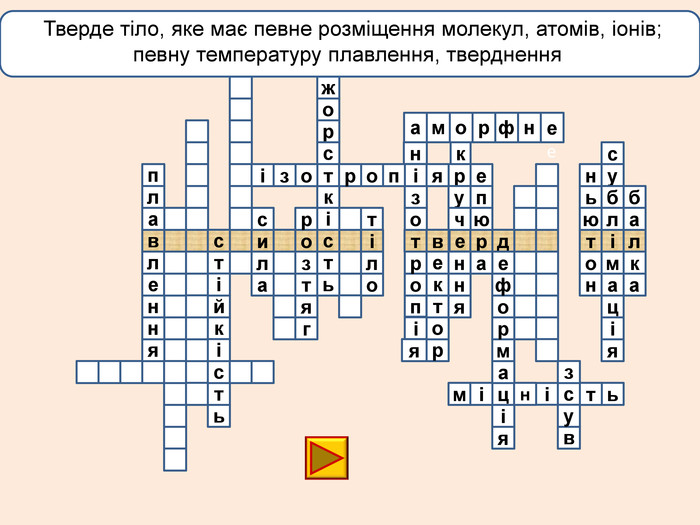
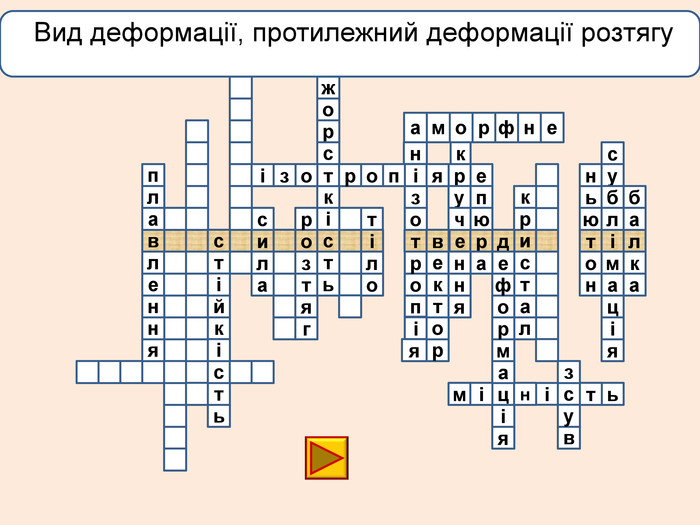
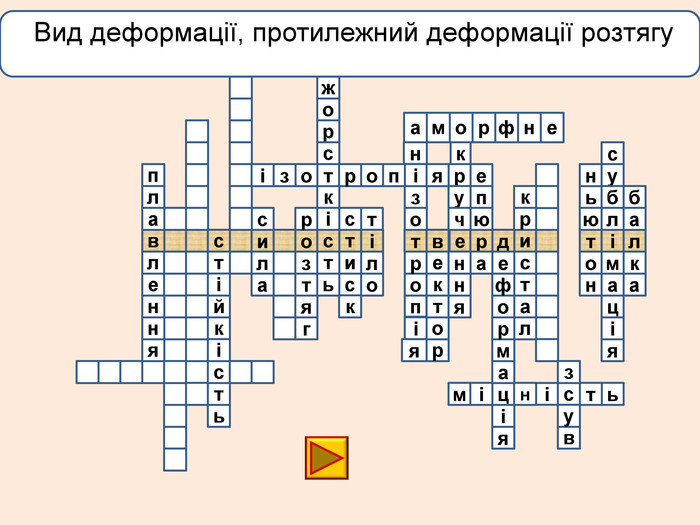
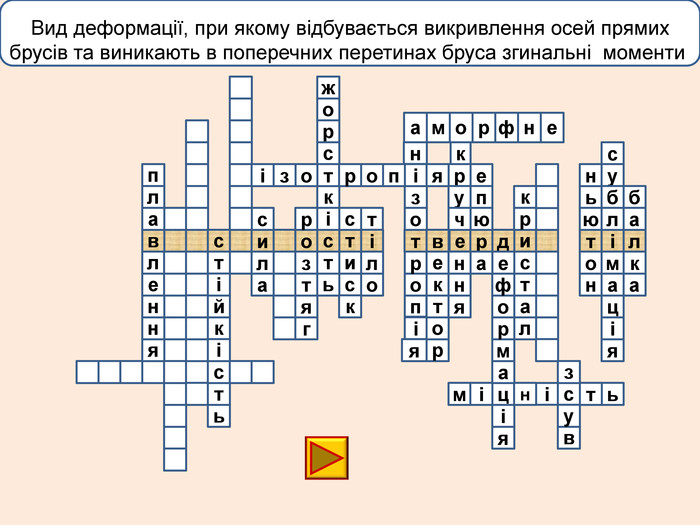
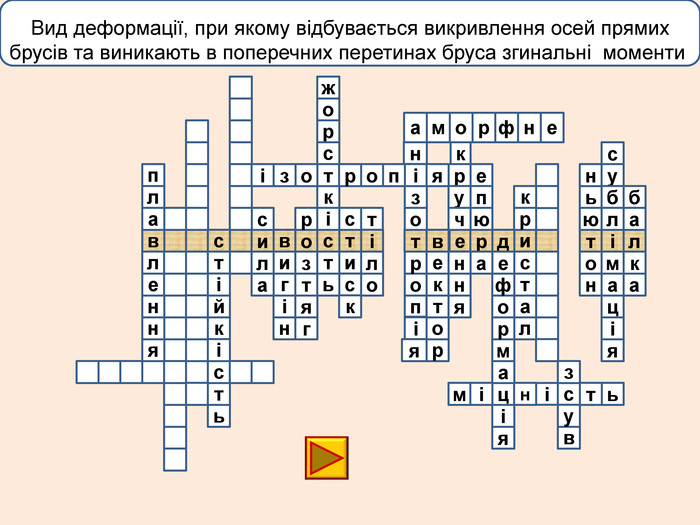
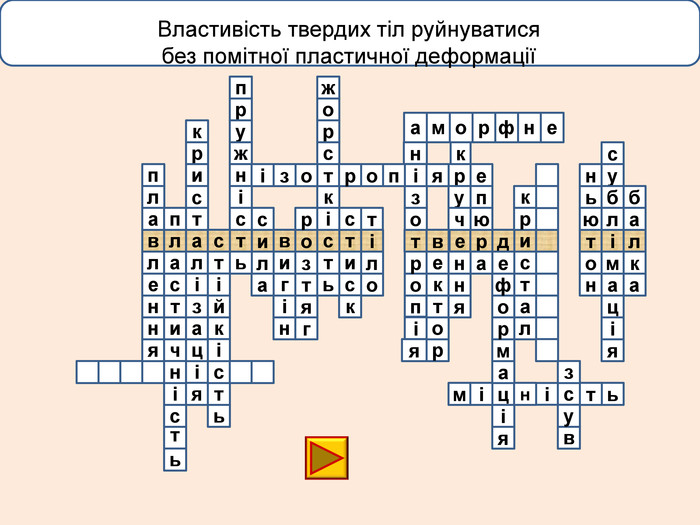
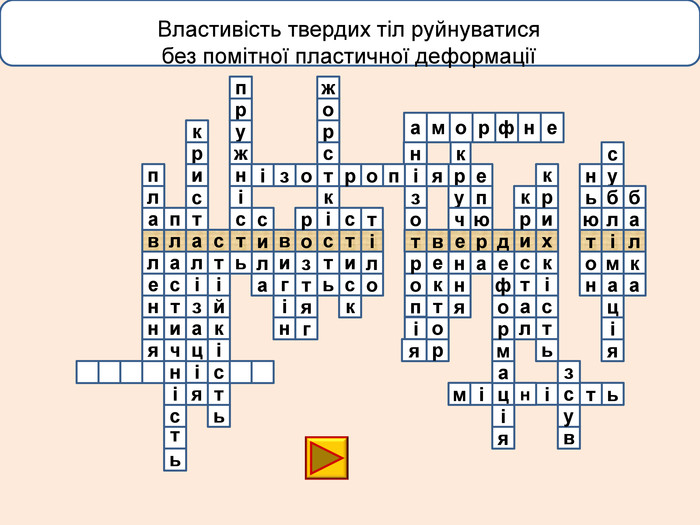
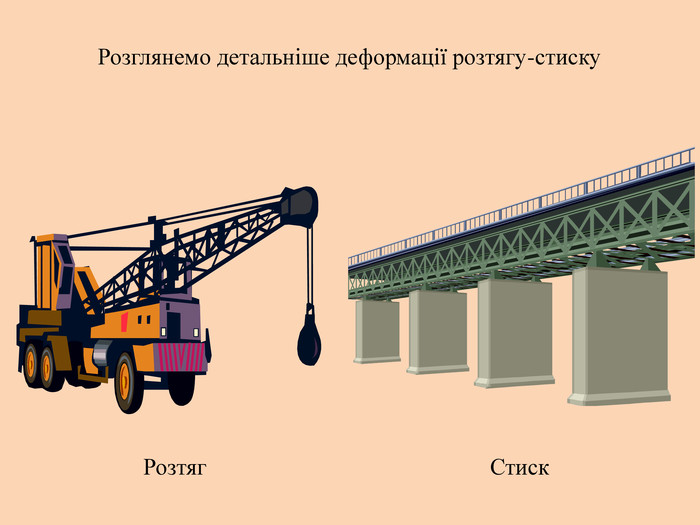
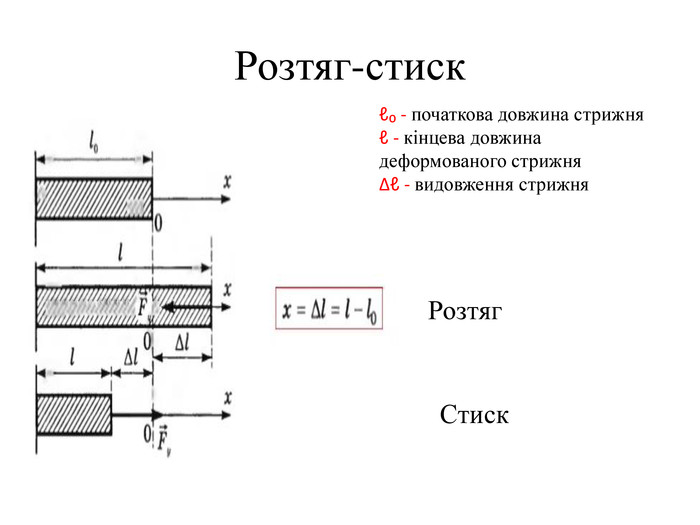
лакбатьюнонісубляіцамдяіцамрофеьтімінсвузвроткерепюаіолтиалссьтжорсківплаяннелстькйітсіітозіпоря. ММ Вид деформації твердого тіла, при якому його розміри вздовж однієї осі збільшуються під дією сил, рівнодійна яких є перпендикулярною до поперечного перерізу тіла і проходить через центр ваги його
лакбатьюнонісубляіцамдяіцамрофеьтімінсвузвроткерепюаіолтиалсогятзрсьтжорсківплаяннелстькйітсіітозіпоря. ММ Вид деформації твердого тіла, при якому його розміри вздовж однієї осі збільшуються під дією сил, рівнодійна яких є перпендикулярною до поперечного перерізу тіла і проходить через центр ваги його
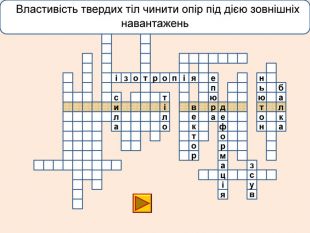
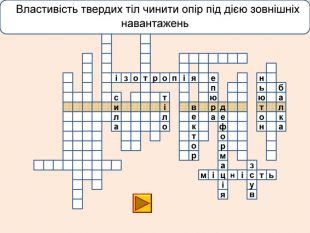
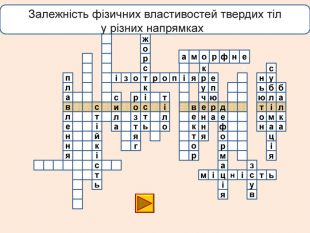
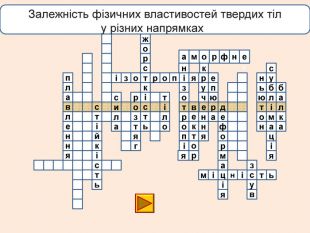
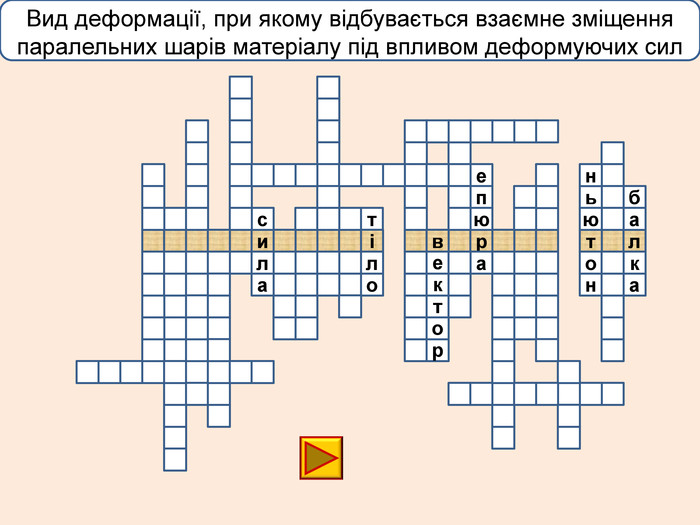
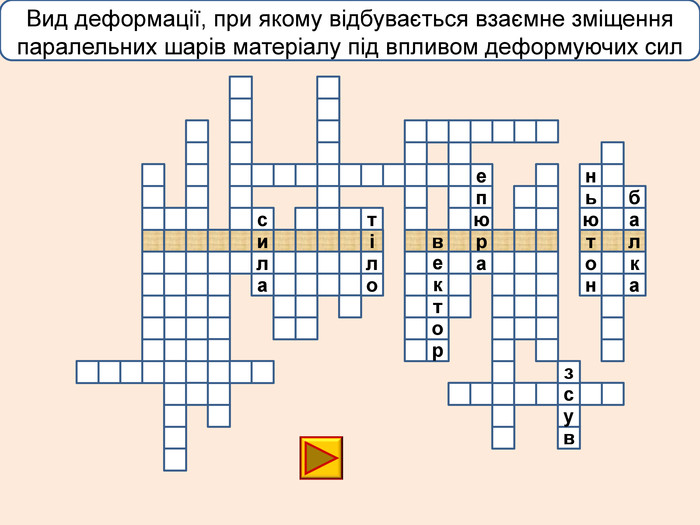
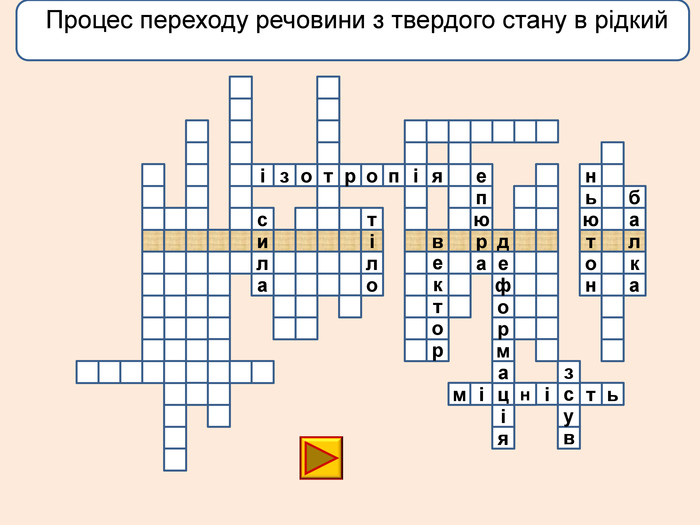
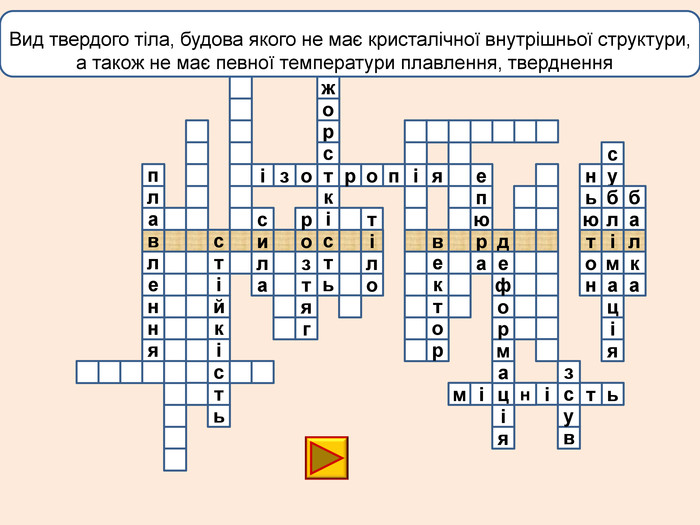
телакбатьюнонісубляіцамхитсіккрьилатскрдяіцамрофеьтімінсвузяіпорвроткерепюаянннкручзоаенфроміолттсисквнігииалсогятзрсьтжорскітьпружнісвплаяннеллпчитсатсіньакрисстіліяцазстькйітсіітозіпоря. ММ Властивість твердих тіл при поступовому збільшенні тиску поступатися дії певних сил і текти як рідина
телакбатьюнонісубляіцамхитсіккрьилатскрдяіцамрофеьтімінсвузяіпорвроткерепюаянннкручзоаенфроміолттсисквнігииалсогятзрсьтжорскітьпружнісвплаяннеллпчитсатсіньакрисстіліяцазстькйітсіплинтьітозіпоря. ММ Властивість твердих тіл при поступовому збільшенні тиску поступатися дії певних сил і текти як рідина
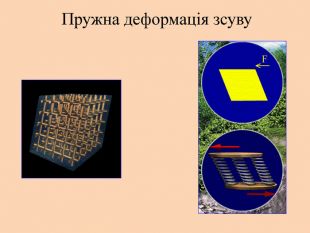
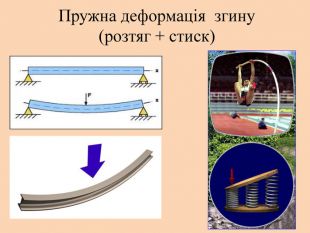
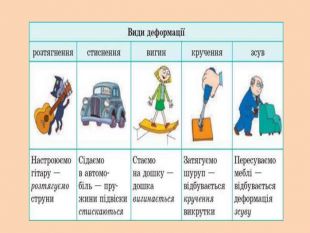
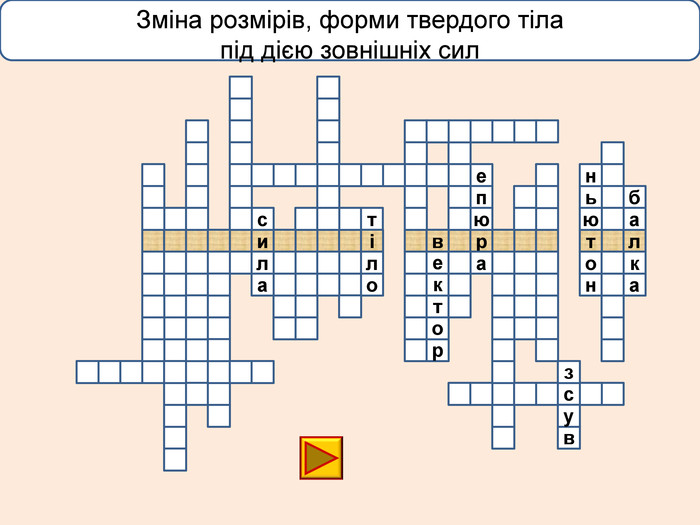
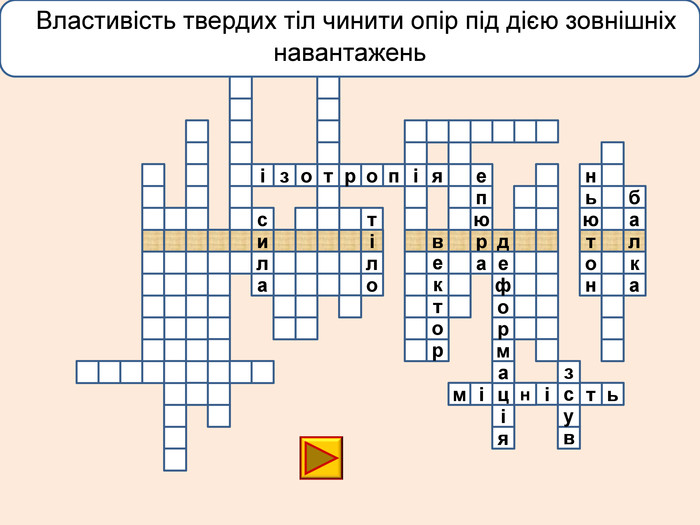
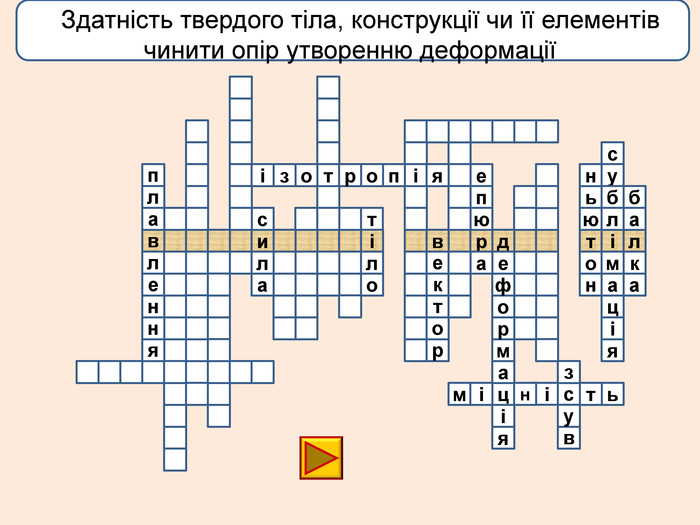
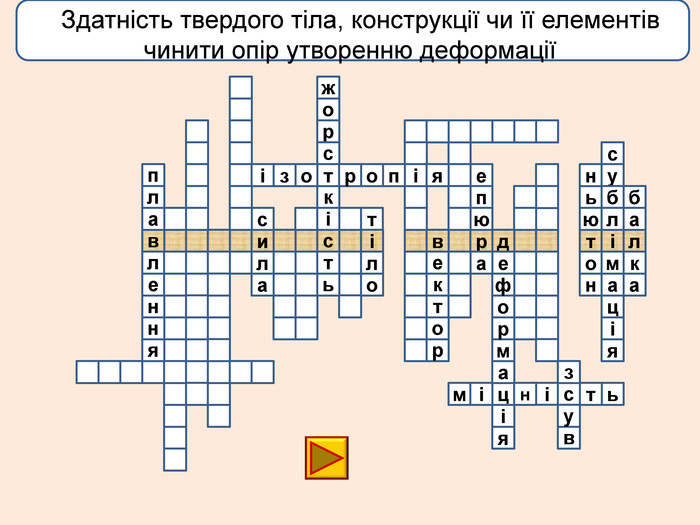
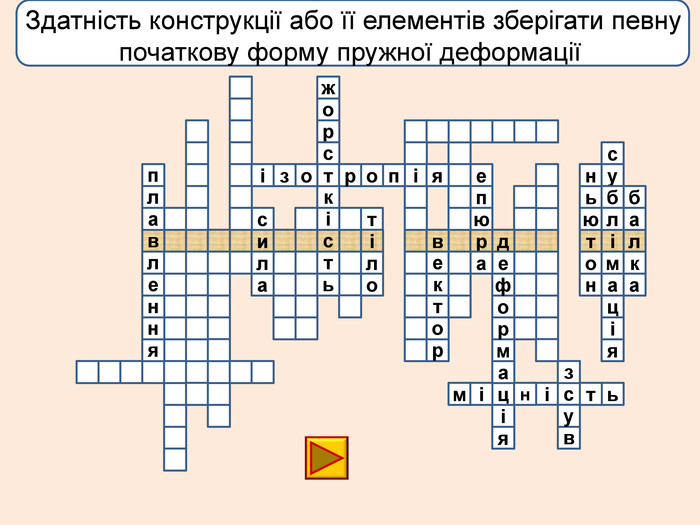
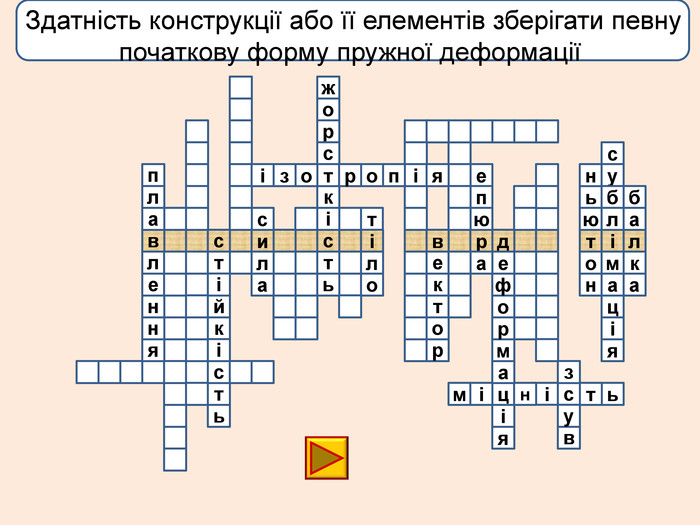
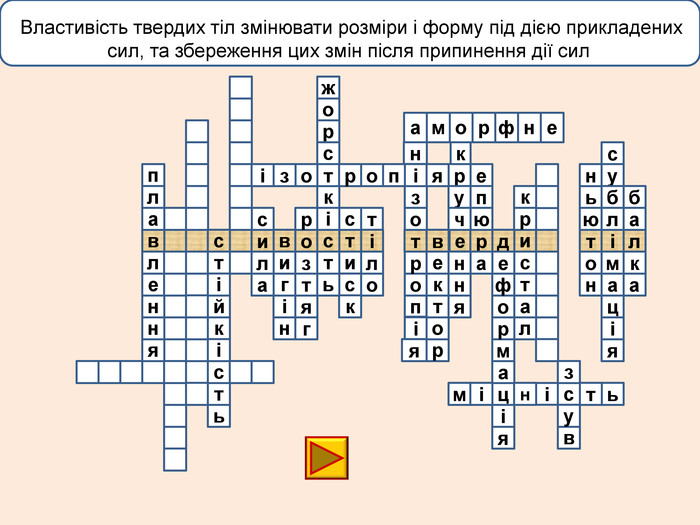
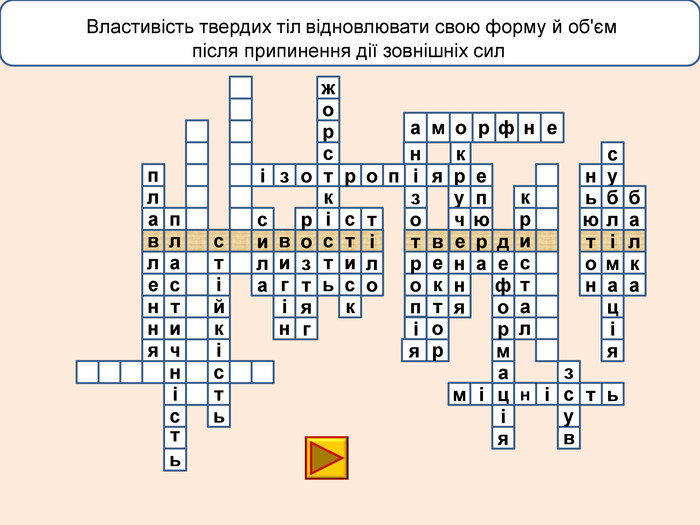
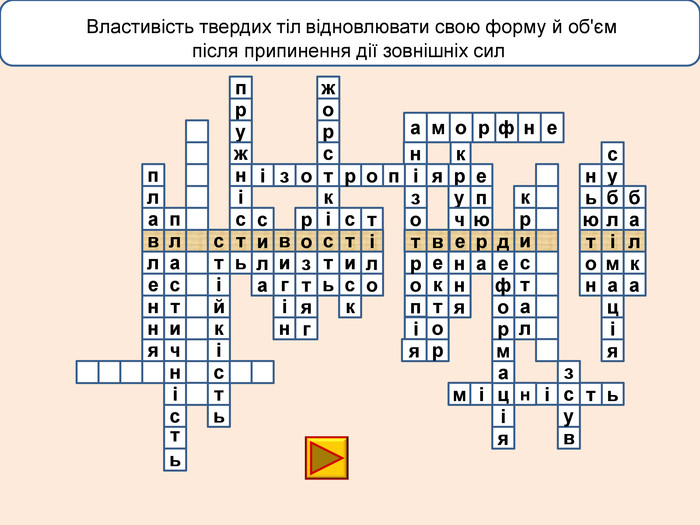
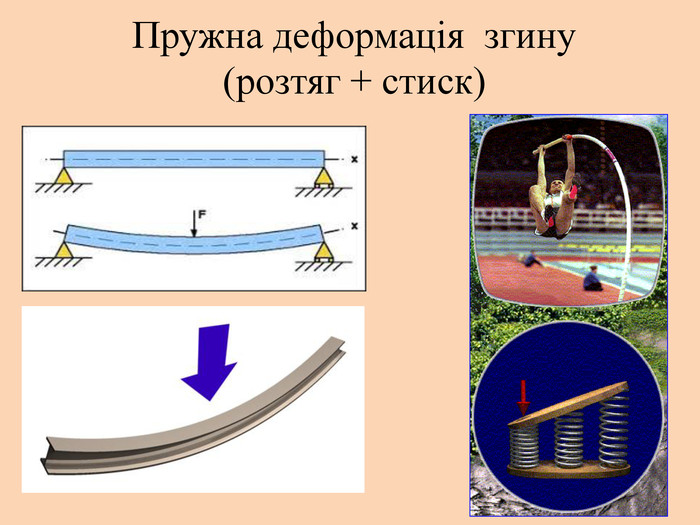
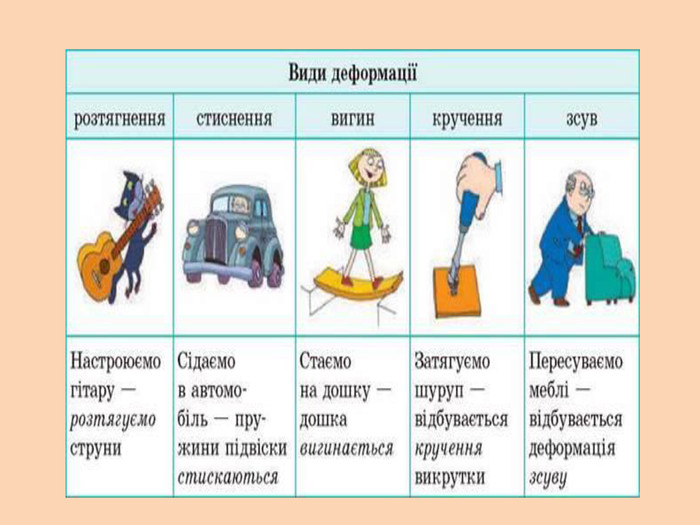
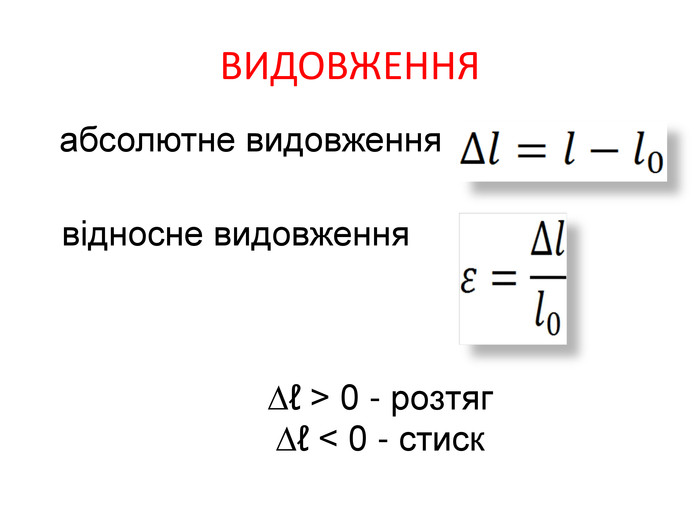
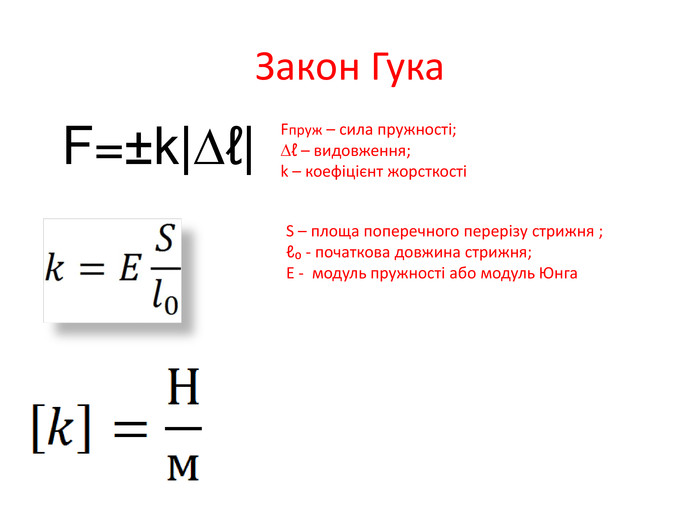
Деформація – зміна розмірів, об'єму або форми твердого тіла під дією зовнішніх. Пружні деформації – деформація твердого тіла, яка зникає після припинення дії сили і тіло повністю відновлює форму та розміри. Пластичні деформації – деформація твердого тіла, яка залишається після припинення дії сили і тіло не відновлює повністю або частково розміри і об'єм.
Метод допустимих напружень. Допустимим напруженням [σ] називається найбільше напруження, при якому забезпечується міцність і довговічність проєктованого елемента конструкції. Граничними називають стани, при яких конструкція, будівля або споруда перестає задовольняти заданим вимогам в процесі зведення або експлуатації.
1. Перевірочний (перевірка на міцність)При заданих значеннях поздовжньої сили і площі поперечного перерізу визначають робоче (розрахункове) напруження і порівнюють його з допустимим напруженням:σ = N/S≤[σ] Значення допустимих напружень для деяких матеріалів при статичній дії навантажень приведені в таблиці (Додаток). Потім обчислюють розбіжність (у відсотках) між фактичним і допустимим значеннями робочого напруження. Якщо перенапруження перевищує 5%, міцність конструкції, яка розраховується, вважається недостатньою. Розрахунки на міцність виконуються в кілька етапів:а) при необхідності визначаються опорні реакції;б) розраховуються внутрішні силові фактори і будуються їх епюри;в) визначаються найбільш навантажені ділянки або перетини бруса;г) залежно від умови задачі виконується необхідний розрахунок.
Розв'язання задачіДля правої частини стрижня небезпечним є перетин І-І, в якому діє поздовжня сила розтягу. Nр=100к. Н, а площа перерізу А1=42∙π/4=12,56см².σ = Nр/А1=100∙10³/12,56∙10¯⁴=79,6∙10⁶Н/м²=79,6 МПа<[σ]р=80 МПа. У лівій стислій частині стрижня поздовжня сила за абсолютною величиною дорівнює Nс=500к. Н і всі перетини небезпечні. А2 = 62 = 36 см2.σ = Nс/А2=500∙10³/36∙10¯⁴=138,9∙10⁶Н/м²=138,9 МПа<[σ]с=150 МПа
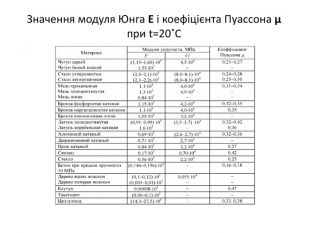
Задача для самостійного розв'язання Сталева штанга довжиною l=4 м має перетин у вигляді квадрата зі стороною а=20 мм. До кінця штанги підвішений вантаж Р1= 80к. Н. Посередині довжини до штанги приварені два швелера і на кожному з них закріплений вантаж Р2=10к. Н (рисунок 3). Модуль поздовжньої пружності стали Е=2·105 Н/мм2, коефіцієнт поперечної деформації μ=0,25. Необхідно:1. Перевірити міцність штанги. 2. Визначити абсолютне та відносне подовження штанги в небезпечному перетині. 3. Визначити абсолютну та відносну зміну поперечного розміру (звуження) штанги в небезпечному перетині. Рисунок 3
Задача для самостійного розв'язання1. Для визначення переміщень необхідно визначити внутрішні зусилля в поперечних перетинах штанги та побудувати епюру поздовжніх сил. Штангу розбиваємо на дві ділянки: верхню та нижню, кожну довжиною l=2м. Провівши перетин I-I та II-II, знаходимо поздовжні сили. Ділянка. I-IДілянка II-IIРисунок 4 Рисунок 5
Задача для самостійного розв'язання2. Визначаємо напруження в поперечних перетинах штанги. Перетин. I-Iσ1 = N1/S=80∙10³/20∙20=80000/400=200 Н/мм²Перетин. II-IIσ2 = N2/S=100∙10³/20∙20=100000/400=250 Н/мм²Будуємо епюри поздовжніх сил та напружень (рисунок 6). Небезпечним є перетин верхньої ділянки, в її межах виникає найбільше робоче напруження. Штанга виготовлена з вуглецевої конструкційної сталі. Допустиме напруження для цього матеріалу:[σр] = 59-245 Н/мм2σ2=250 Н/мм2> [σр] = 59-245 Н/мм2 Зіставляючи напруження в межах ділянки II-II з допустимим, виявляємо, що має місце перенапруження.250-245/245∙100%=0,02=2%Таке незначне перенапруження ( не вище 5%) може бути допущено. Висновок: міцність штанги забезпечена. Рисунок 6
Задача для самостійного розв'язання3. Визначаємо поздовжню деформацію на небезпечній ділянці. Абсолютна деформація (абсолютне подовження):Δℓ=N∙ℓ/E∙S=100000∙2000/2∙10⁵∙400=2,5мм=0,25см=0,0025м. Відносна деформація (відносне подовження):ε=σ/Е=250/2 ∙10⁵=0,00125=0,125%Висновок: подовження штанги під дією заданих сил становить 0,125 % її початкової довжини. 4. Визначаємо поперечну деформацію на небезпечній ділянці. Відносне звуження:εḻ=µ∙ε=0,25∙0,00125=0,0003125=0,03125%Абсолютна зміна боку квадратного перетину: Δа=lεḻl∙а=0,003125∙20=0,00625мм. Висновок: поперечна деформація штанги під дією заданих сил настільки незначна, тому при практичних розрахунках на розтяг або стиск, її впливом на зміну поперечних перерізів елементів конструкцій можна знехтувати.


про публікацію авторської розробки
Додати розробку