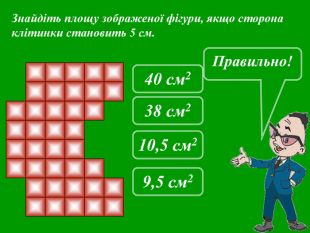
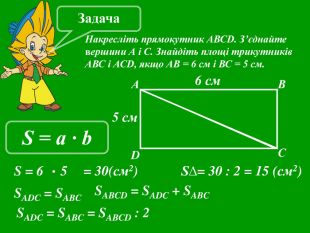
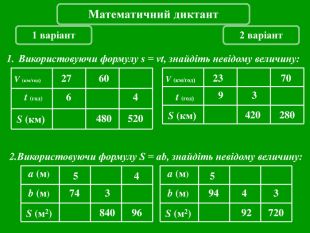
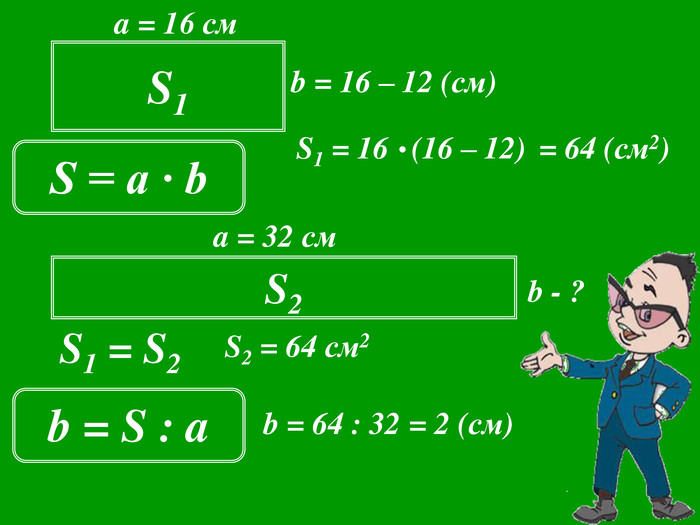Презентація до уроків математики в 5 класі "Формули"
Про матеріал
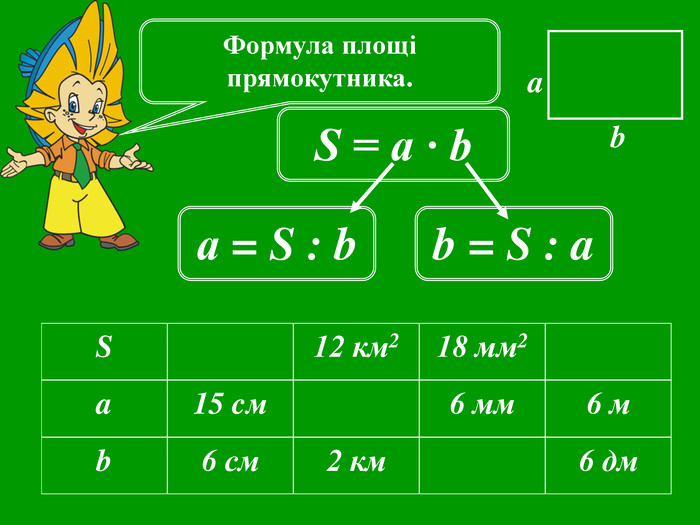
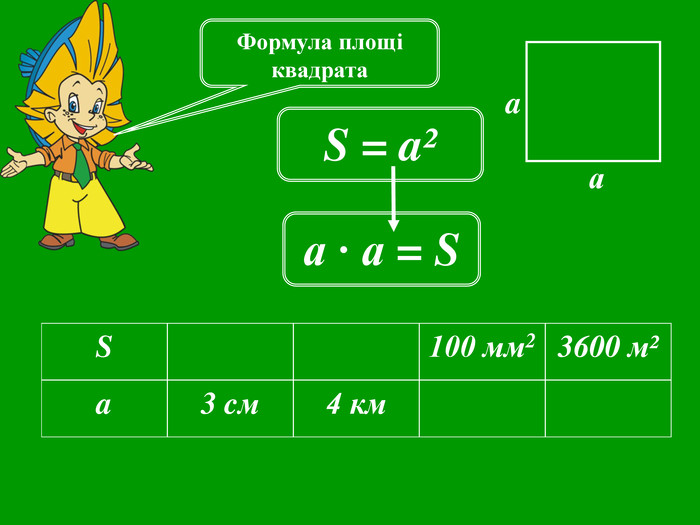
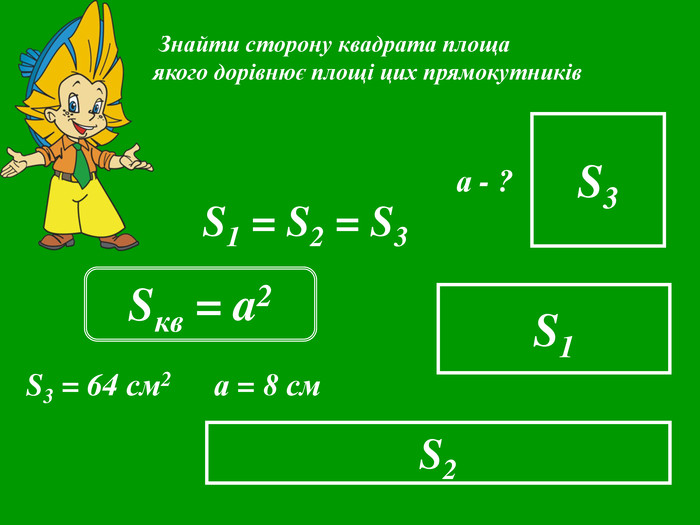
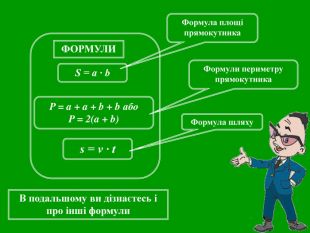
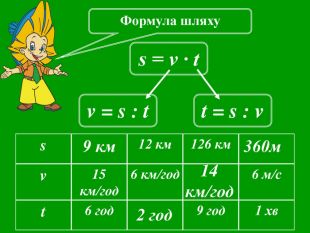
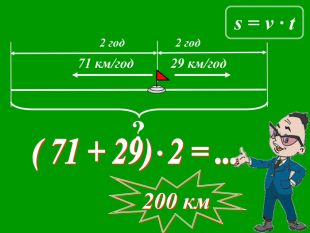
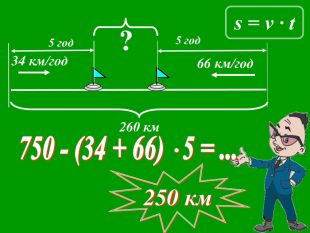
Презентації уроків з математики розроблені відповідно до підручника Істер О. С. Математика, 5 клас, але можна успішно використовувати і до інших авторів.
Кожна презентація побудована у вигляді опорної схеми із залученням анімаційних об'єктів. Це «зволожує» математичну «сухість» матеріалу, а також викликає в учнів додатковий інтерес, враховуючи їх вікові особливості. Крім того, кінематика презентацій будить в учнів різні види сприйняття і запам'ятовування інформації.
Розроблені презентації можна, при потребі, доповнити або перебудувати, враховуючи особливості викладання в тому чи іншому класі.
Перегляд файлу
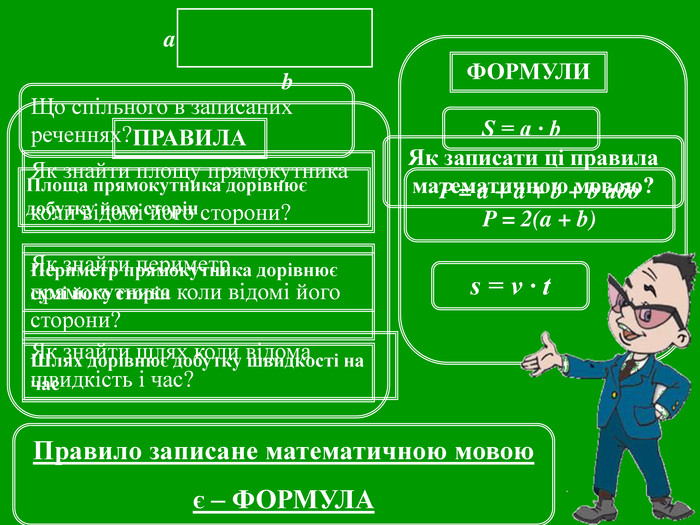
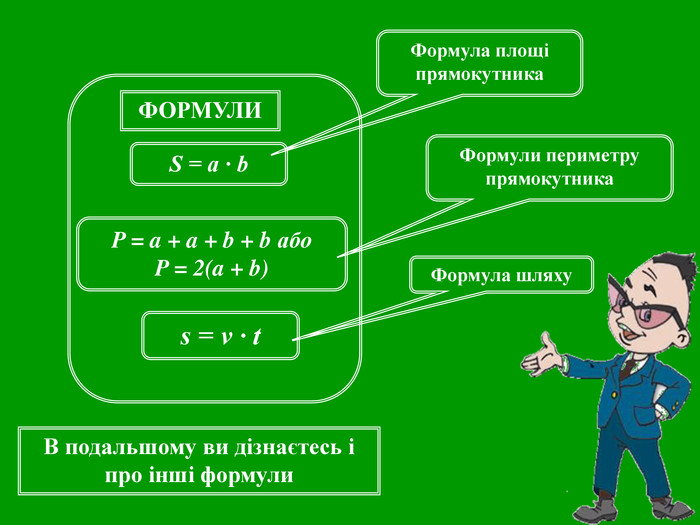
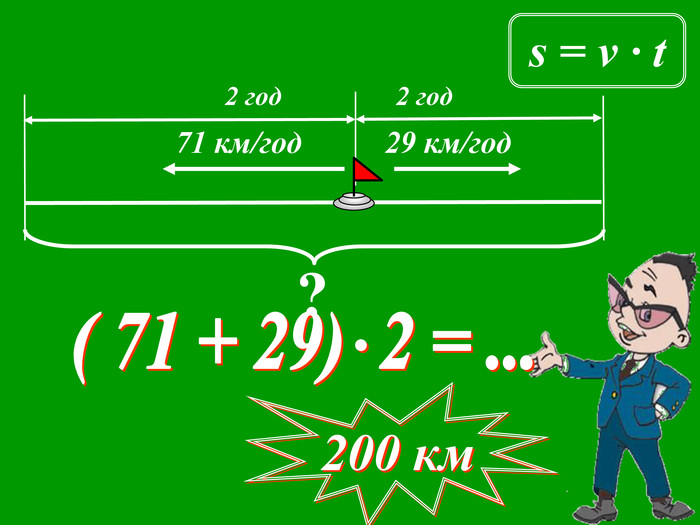
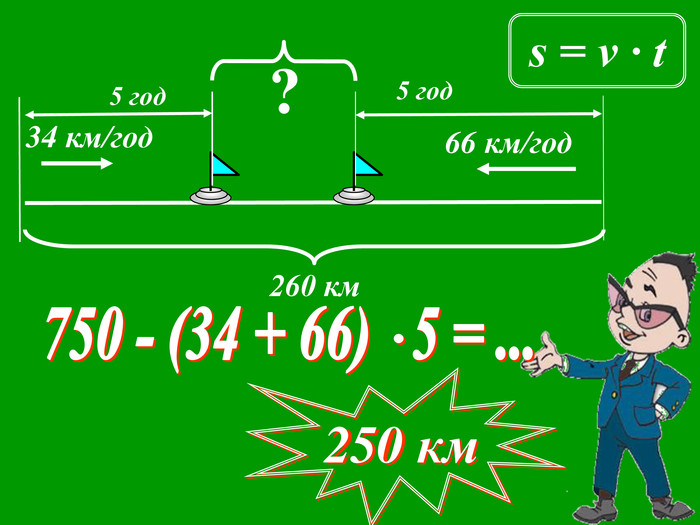
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку