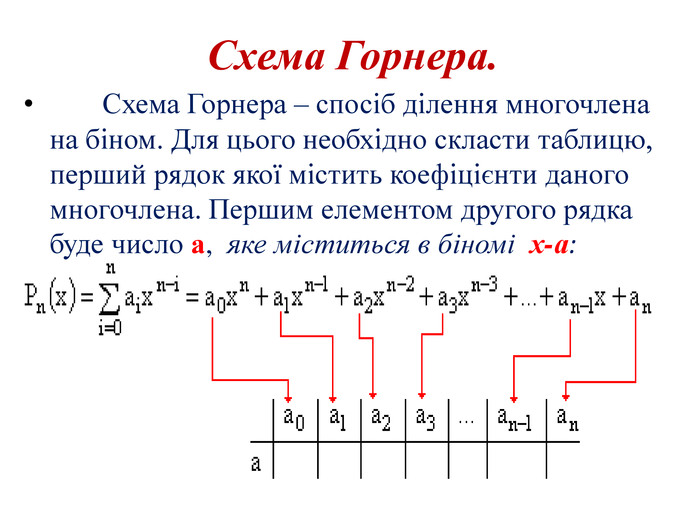
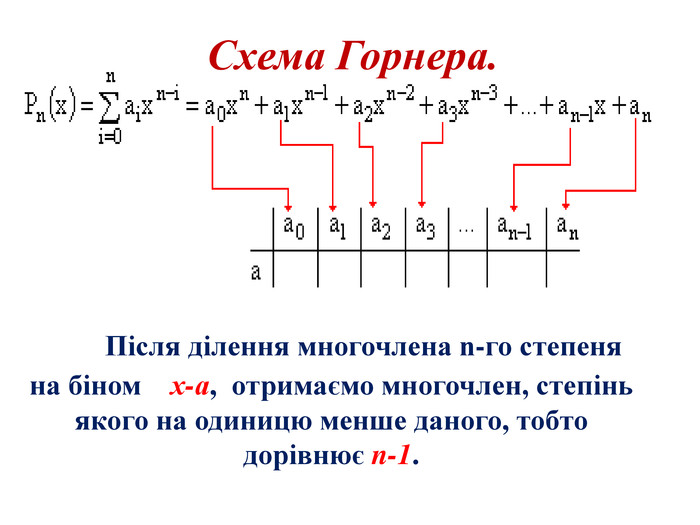
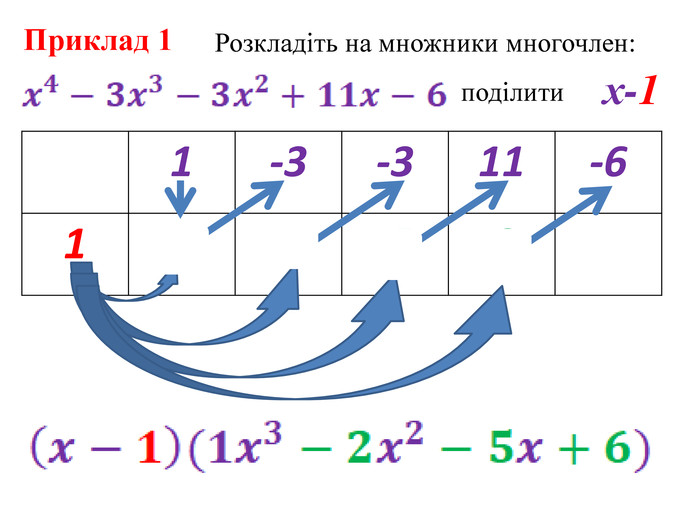
Презентація до уроку алгебри для 8 класу, тема: "Схема Горнера"
Про матеріал
Даний матеріал до уроку може бути використаний при дистанційному навчанні. Створений для проведення уроку в формі ZOOM конференції. презентація містить елементи теоретичного матеріалу, приклади розв'язування вправ та вправи для колективного розв'язання. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (підручник для класів із поглибленим вивченням математики) 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 3. Основи теорії подільності Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку