Презентація до уроку алгебри в 11 класі 'Степенева функція'

Урок узагальнення по темі ‘Показникова та логарифмічна функції’

“ Знання збільшуються, а вміння вдосконалюються, коли ними ділишся”Оноре де Бальзакфранцузький письменник 2 Девіз урокуІсторична довідка. Питання, пов'язане з показниковою функцією, розробляв Леонард Ейлер (див. фото). У двох розділах своєї праці “Вступ до аналізу” він описав “показникові та логарифмічні кількості”. Навіть і сам показник може бути показниковою “кількістю”.Іранський математик ал-Караджі розглядав рівняння і нерівності відносно деякого степеня невідомого.

Узагальнити і систематизувати знання про показникову та логарифмічну функціїУдосконалити вміння розв’язувати показникові і логарифмічні рівняння та нерівності, застосовуючи властивості показникової і логарифмічної функцій. Мета уроку

Перевірка домашнього завдання

Мозковий штурм під девізом : «Хай живе теорія»

Яка функція називається показниковою?Яка область значень показникової функції?При якій умові показникова функція є зростаючою, а при якій спадною?4. Які з наведених ескізів відповідають графікам показникових функцій:

Функція, , називається показниковою з основою а. Показникова функція Графік функції. Крива називається експонентою7

Які з перерахованих функцій є показниковими?..8

На якому з малюнків зображений графік показникової функції?9

Властивості показникової функціїD(f)=(-∞; +∞)D(f)=(-∞; +∞)Е(f)=(0; +∞)Е(f)=(0; +∞)ЗростаєСпадаєНеперервна Неперервна Обмежена знизу. Обмежена знизу. Випукла вниз. Випукла вниз. Диференційовна. Диференційовна10

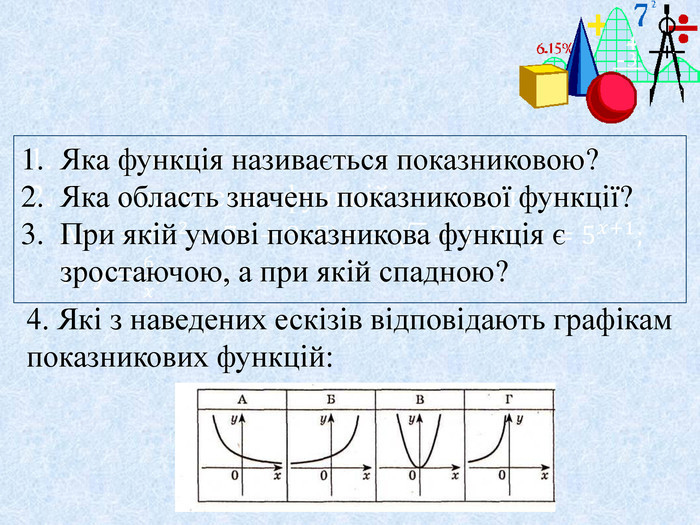
11 Показникові рівняння Показниковими рівняннями називаються рівняння видуі рівняння, які зводяться до цього виду. Основні методи розв’язання показникових рівнянь. Функціонально-графічний Заснований на використанні графічної ілюстрації чи окремих властивостей функції. Метод урівнювання показників Заснований на застосуванні теореми 17.1. та наслідка з неї (пункт 17 підручника) Рівняння рівносильне рівнянню або f(x) = g(x), де а>0, а≠1. Метод введення нової змінної

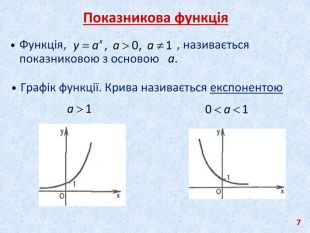
12 Показникові нерівності Показниковими нерівностями називаються нерівності видуі нерівності, які зводяться до цього виду. Розв'язування показникових нерівностей. Теорема 18.1: Показникова нерівність рівносильна нерівності f(x) > g(x), якщо а > 1 ;рівносильна нерівності f(x) < g(x), якщо 0 < а < 1. Приклади

1) 2) 3) Між якими цілими числами розміщений корінь другого рівняння? 13 Розв'язати показникові рівняння

1) 2) 3)4) Пояснити алгоритм розв’язування нерівностей.5) Які властивості показникової функції застосовуємо при розв’язуванні показникових рівнянь та нерівностей?14 Розв'язати показникові нерівності

15 Знайти помилку!1) Розв'язати рівняння2) Розв'язати нерівність

1 Означення логарифма.2. Яка функція називається логарифмічною?3. Яка область значень логарифмічної функції?4. Властивості логарифма.5. Які рівняння називають логарифмічними?6. Чи існує логарифм від’ємного числа?

Функція виду y=logax , де a > 0, a ≠ 1. Логарифмічна функція

Логарифм та його властивості.

З наведених рівнянь виберіть логарифмічні:1) log 2(x+3)=8 2) xlgx=1003) 2ln3 + x3=10 4) log22x +2 log2x=05) lg100 + lg 0,001 – (2x+4)=0 6) log3(x+2)+log3(2x-1)=log38

На якому з малюнків задано функцію у = log 0,4 x ?

1. Розв’язати рівняння 2х +2х-3=722. Розв’язати нерівність log2/3(6-х)≤log2/3(х+1)3. Розв’язати рівняння 9x -2∙3x = 63 Розв’яжіть в парах

Розв’язати рівняння log4log2log3(2x-3)=0,5 Розв’яжіть самостійно

Підготовка до ЗНО23 Тест- контроль!

Відповіді до тестів{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}123456789101112 ГВААВВАВВБВА

Домашнє завдання. Повторити теоретичний матеріал з теми, підготуватися до контрольної роботи. Розв’язати: 1. log22x +2 log2x=0 2. 3х+1 - 2∙3х-2 ›75 3. (0,3)4-2х≤ (0,09)4х+10 4. 5х=3х 5. 3∙4х -5∙6х +2∙9х=0

Використання показникової функції в різних фізичних процесах, вгалузях техніки і в природі

Побутовий приклад!  

Радіоактивний розпад  

Розмноження бактерій  

Приріст деревини  

Зміни атмосферного тиску  

Також…. 

Відомості про використання логарифмів К. Ціолковський вивів формулу для розрахунку абсолютної швидкості, якої досягне ракета, коли з неї витече все паливо. Ця формула містить логарифм.

Відомості про використання логарифмів. Властивості будови слухового апарату людини відповідають властивостям логарифмічної функції. Тому діапазон звуків, що сприймає вухо, низький – від шелесту листя до гуркоту грому.

ХІМІЯ Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену р. Н= - lg С( Н+)

Логарифмічна функція моделює такі процеси:закон зміни роботи газу;закон зміни сили відчуття від сили збудження (психофізичний закон Вебера);закон зміни тиску від зміни висоти;тривалість хімічної реакції;залежність збільшення величини банківського вкладу від пройденого часу.

ФІЗИКАУ гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними.

Логарифмічна спіраль у природі

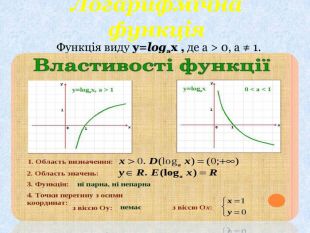
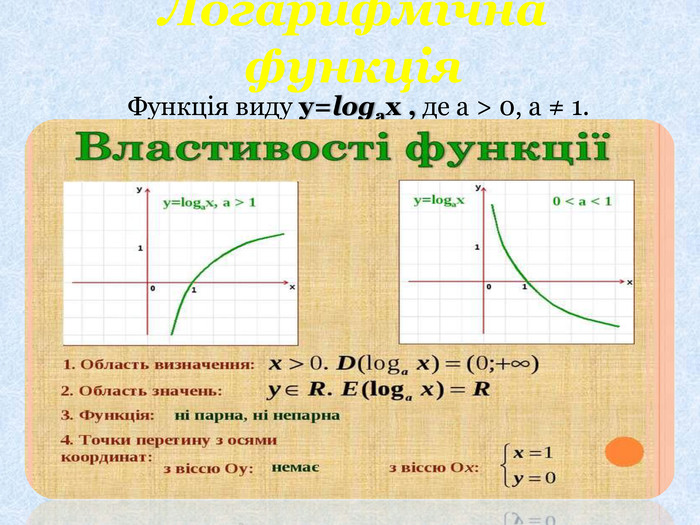
Иоганн-Вольфганг Гете вважав:«Логарифмічна спіраль є математичний символ життя і духовного розвитку»Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння, закручує нитки навколо центра по логарифмічних спіралях.

Рефлексія. Сьогодні на уроці ми…Найважливішим на уроці для мене було…Найбільше зацікавило…Найскладнішим для мене було…Щоб усунути прогалини в знаннях, я маю…