Презентація до уроку геометрії в 7 класі "Задачі до розділів І-ІІ."
Про матеріал
Презентації до уроків геометрії розроблені відповідно до підручника Істер О. С. Геометрія, 7 клас, але можна успішно використовувати і до інших авторів.
Старий-добрий PowerPoint демонструє чудові можливості. Кінематика презентацій дає можливість точно візуалізувати методику викладання геометрії.
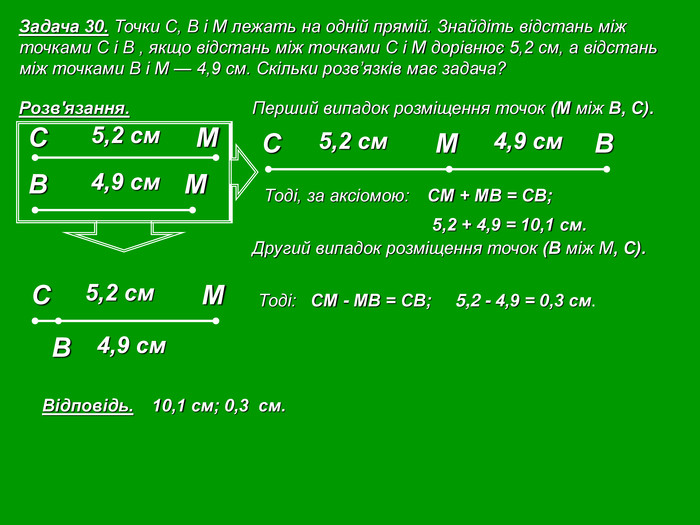
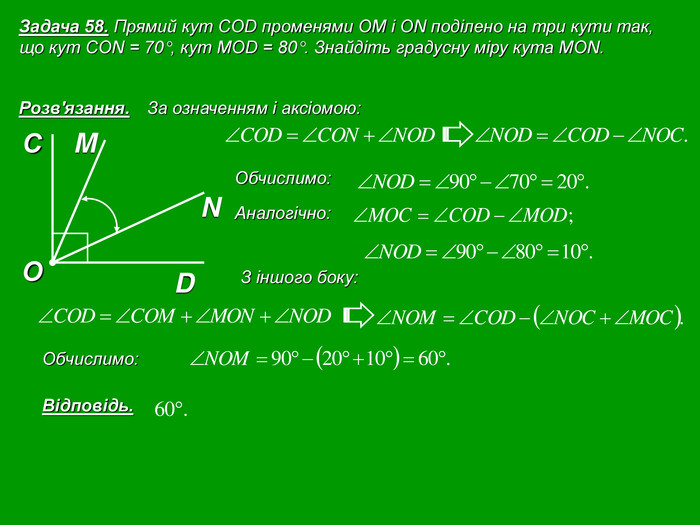
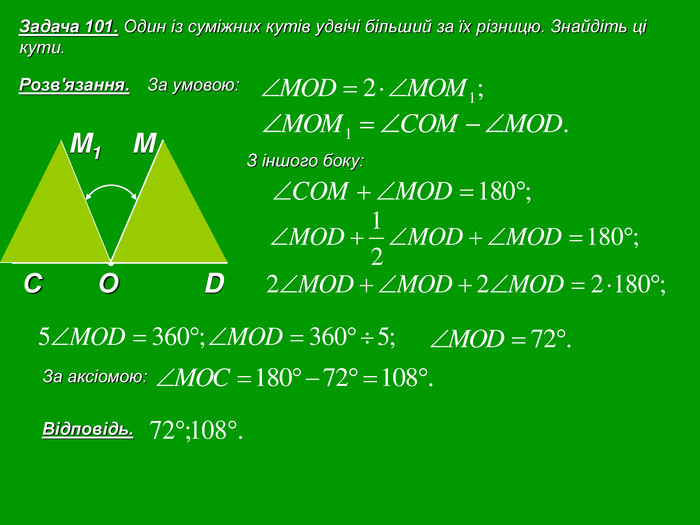
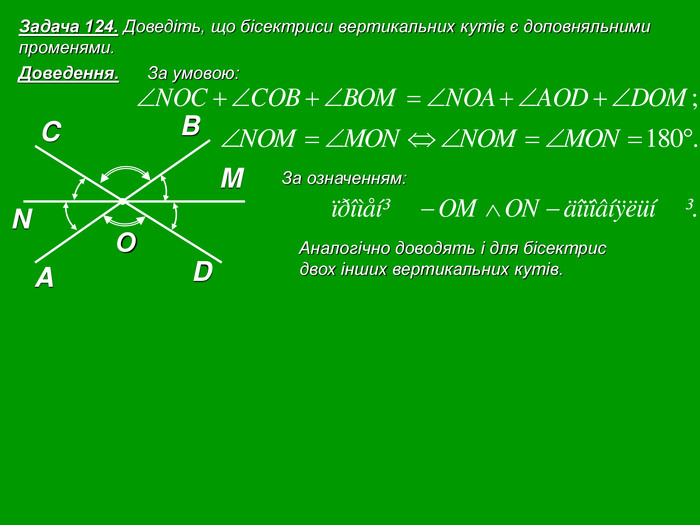
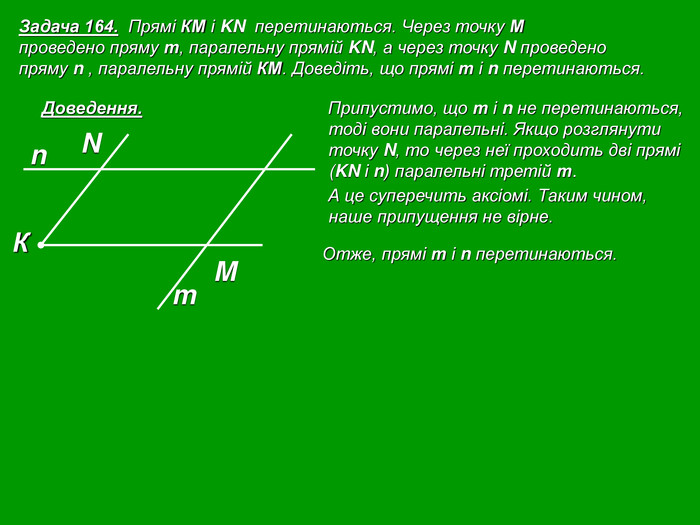
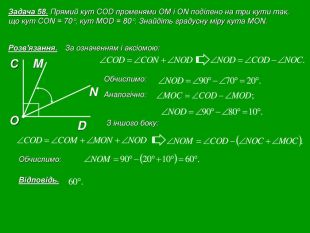
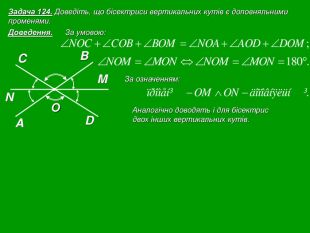
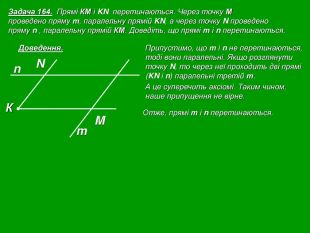
Кожна презентація побудована у вигляді опорної схеми.
Розроблені презентації можна, при потребі, доповнити або перебудувати, враховуючи особливості викладання в тому чи іншому класі.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку