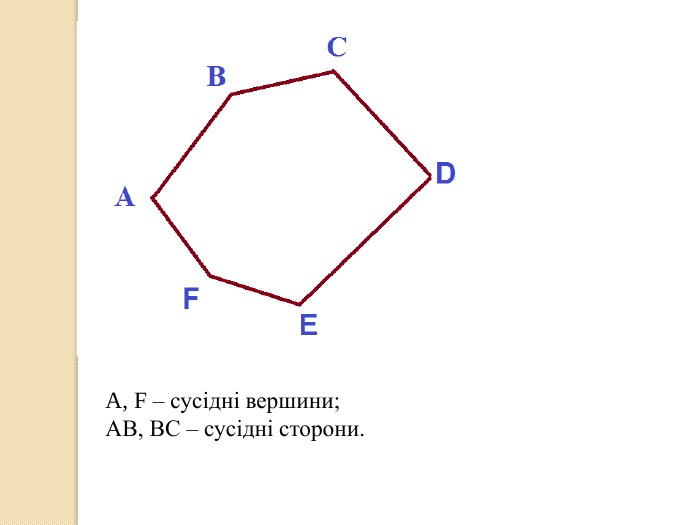
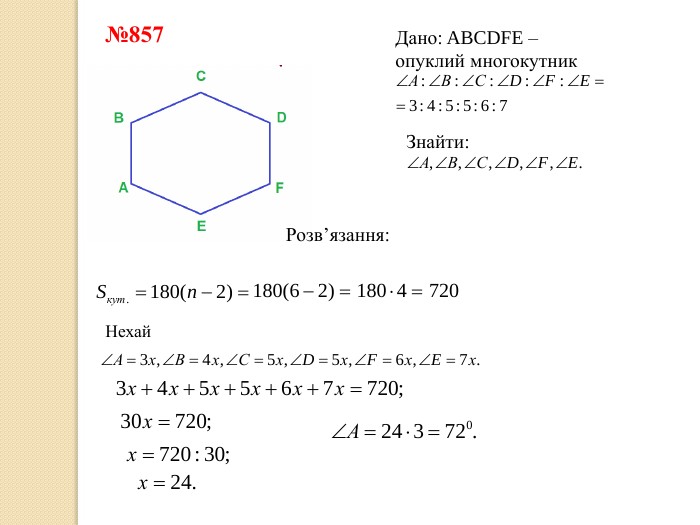
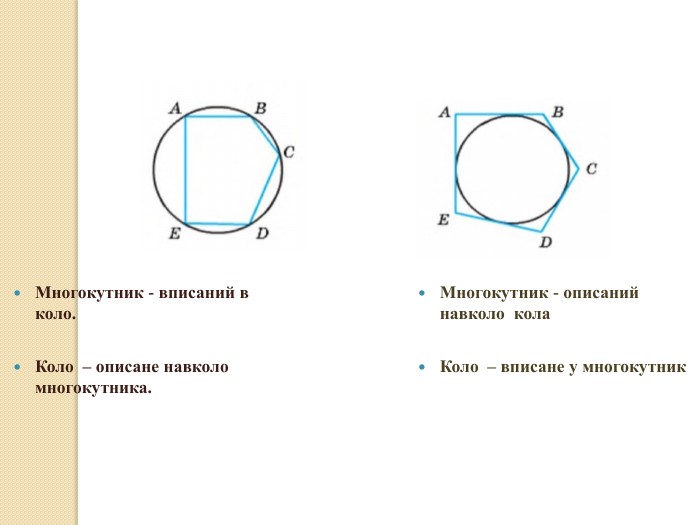
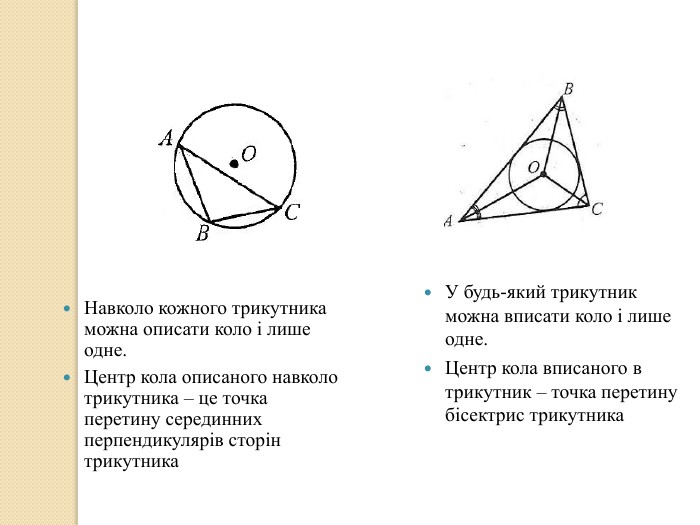
Презентація до уроку "Многокутник. Вписані та описані многокутники"
Про матеріал
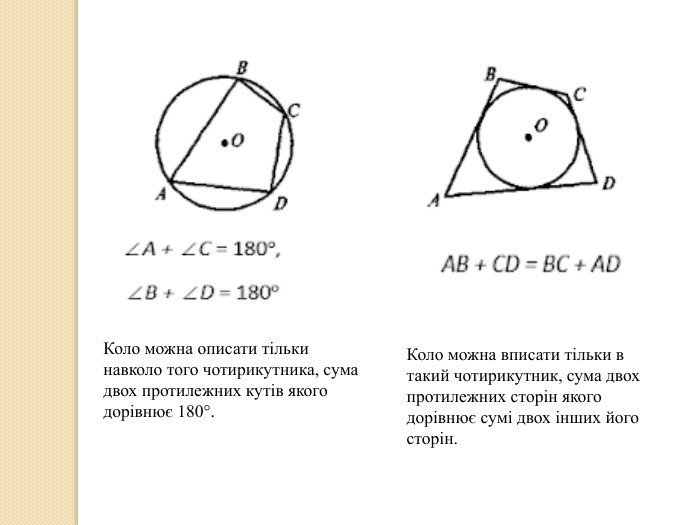
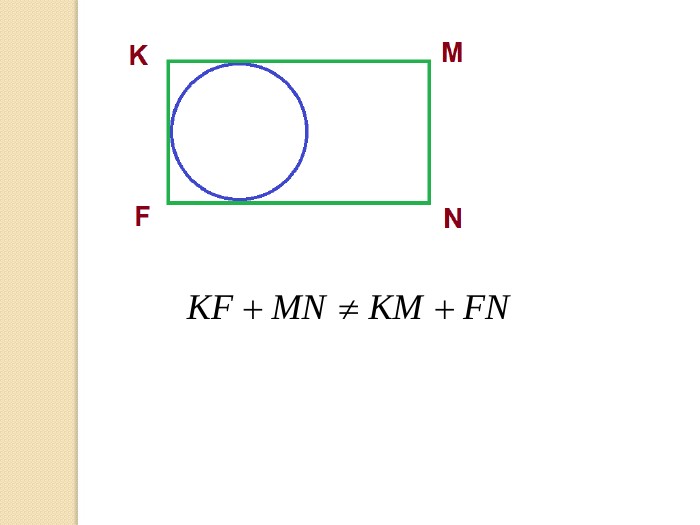
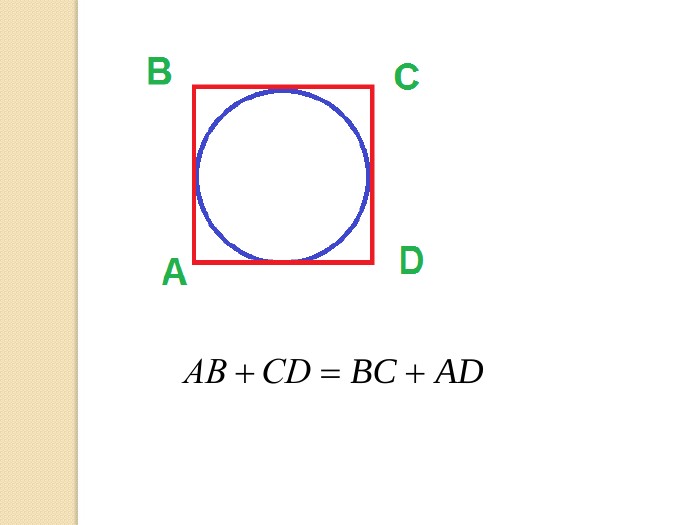
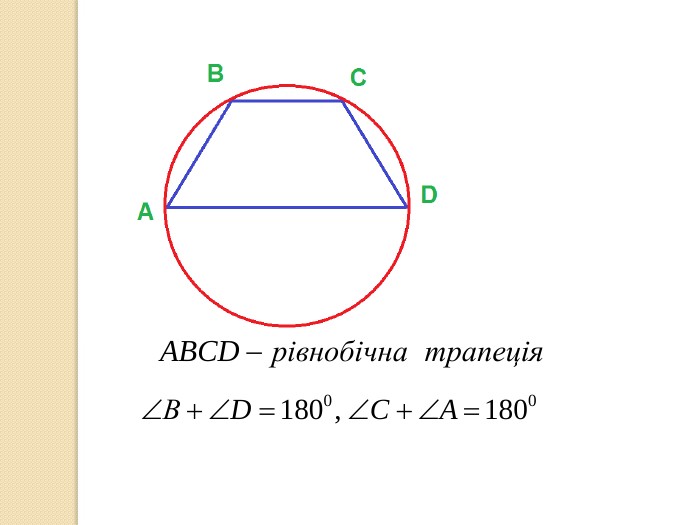
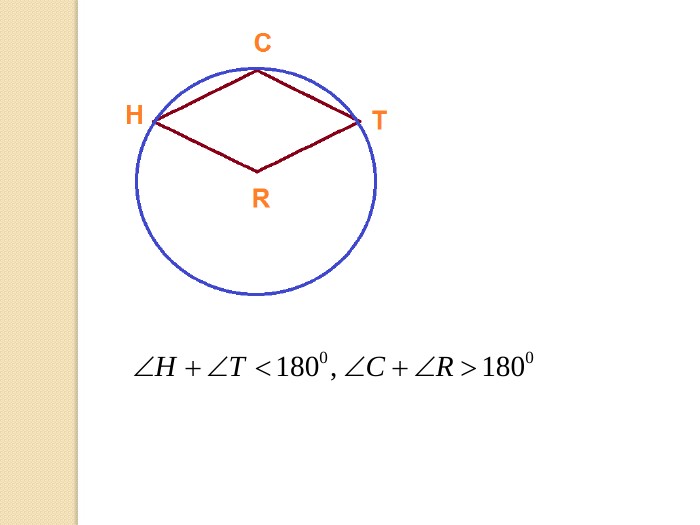
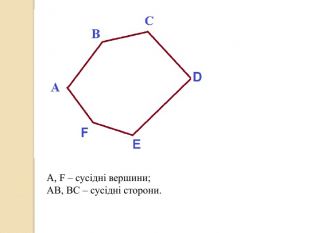
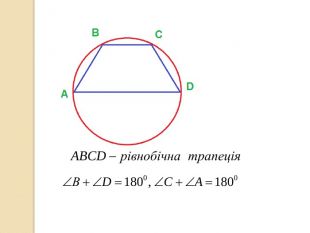
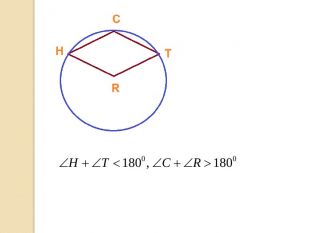
У презентації учні знайомляться з поняттям многокутника, формулою суми кутів опуклого многокутника, необхідними умовами вписання многокутника у коло та описання многокутника навколо кола. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку