Презентація до уроку: "Застосування похідної до дослідження функцій та побудови графіків функцій"
Про матеріал
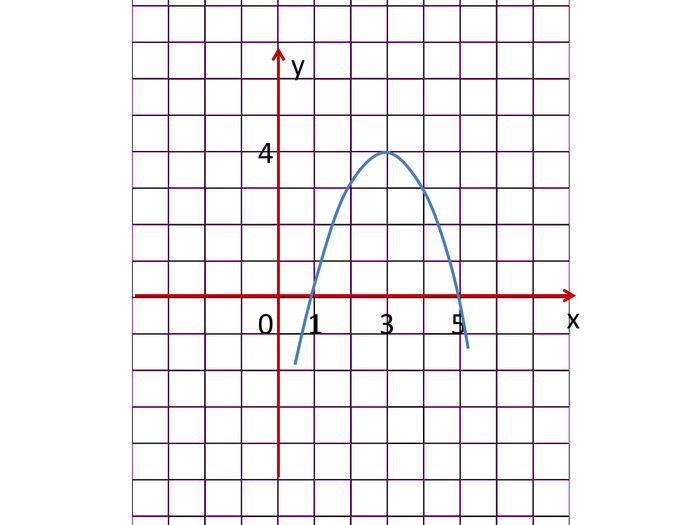
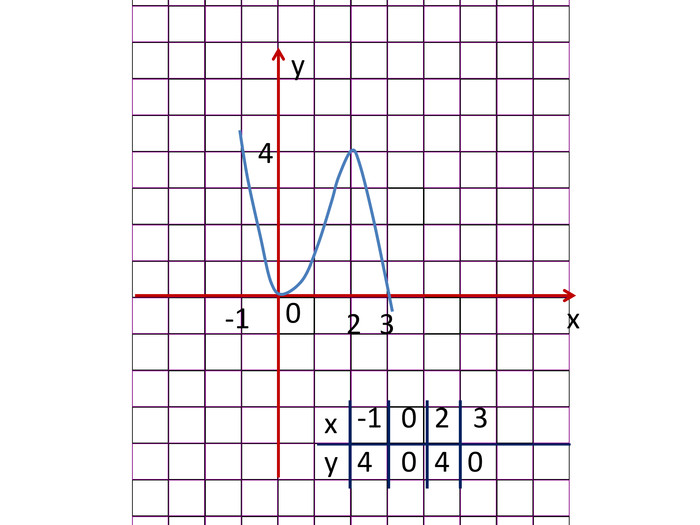
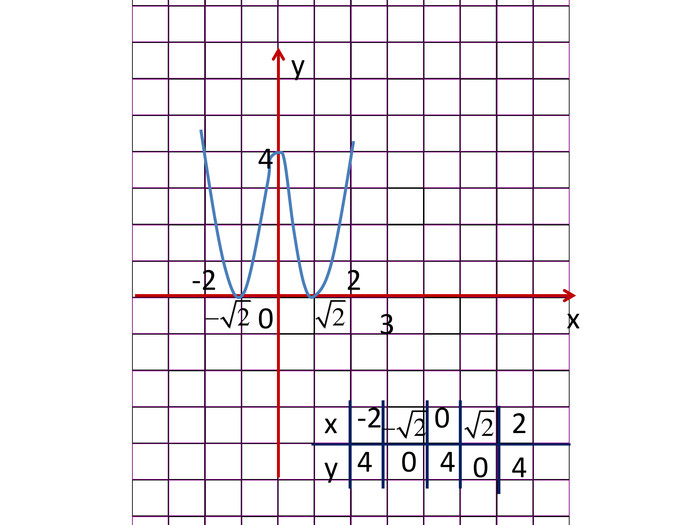
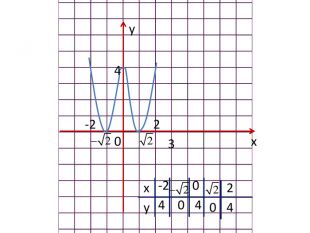
Розробка містить приклади застосування похідної до дослідження функцій та побудови графіків функцій за певним алгоритмом Зміст архіву
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку