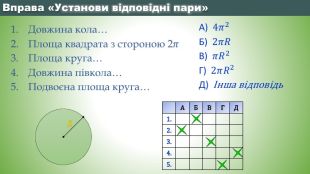
Презентація до уроку "Застосування властивостей геометричних тіл до моделювання реальних процесів"

Застосування властивостей геометричних тіл до моделювання реальних процесів01.11.2022

Обчислити розхід матеріалів та їхню вартість для монтажу каркасу зерносховища з оцинкованого металу. До нас звернувся з проханням фермер

По горизонталі: Геометричне тіло, яке утворюється при обертанні прямокутника навколо однієї з сторін. Фігура, утворена обертанням прямокутного трикутника навколо його катета. Відрізок, який з’єднує дві точки поверхні кулі і проходить через центр. Циліндр, твірні якого перпендикулярні до основи. Поверхня кулі. Тіло, яке складається з усіх точок простору, що знаходяться на відстані, не більшій за дану від деякої точки. Пряма, яка проходить через висоту тіла обертання. По вертикалі: Точка, від якої рівновіддалені всі точки сфери.8. Відстань між основами циліндра. Відрізок, який сполучає будь-яку точку кола з центром. Яка кількість точок конуса.1     9  2    3       8 4      10 5       6    7    циліндрдіаметрконуспрямийсферакулявісьбезлічцентрвисотарадіус. Молодці !

Вправа «Установи відповідність»https://learningapps.org/16530691

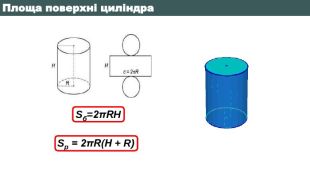
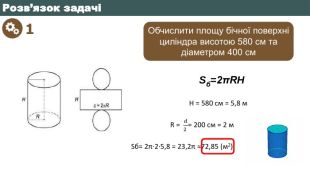
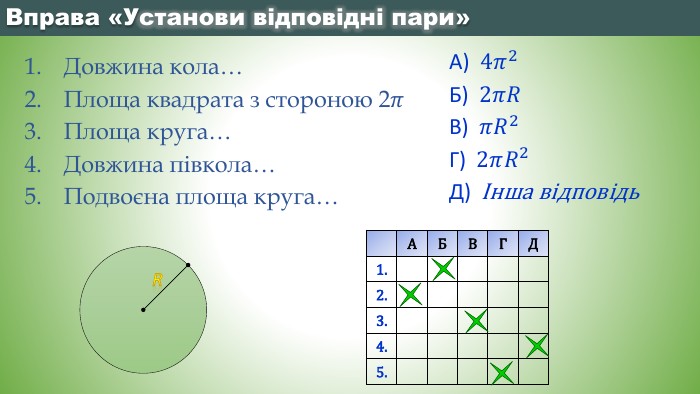
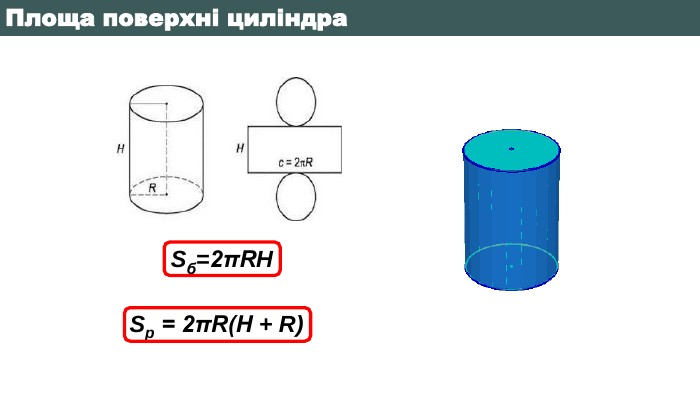
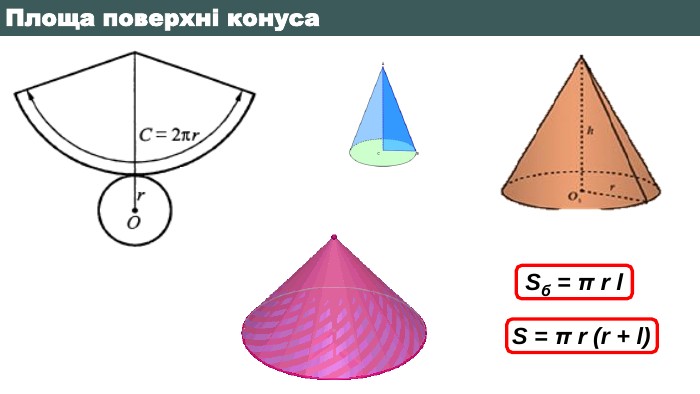
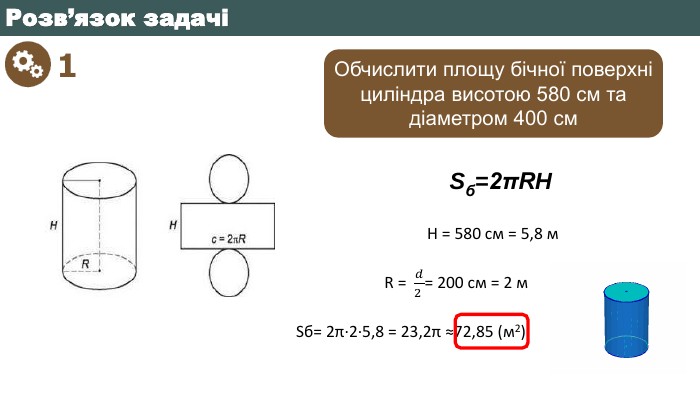
Що являє собою розгортка бічної поверхні циліндра?123451234512345 Що називається твірною циліндра?Взаємне розміщення осі циліндра з твірними. Яку фігуру треба обертати і навколо чого, щоб утворився циліндр?Яка фігура утворюється в осьовому перерізі циліндра, якщо діаметр основи рівний висоті циліндра?Яку фігуру треба обертати і навколо чого, щоб утворився конус?Який конус називається рівностороннім?Яка фігура утворюється в осьовому перерізі зрізаного конуса?Що являє собою розгортка бічної поверхні конуса?Висота конуса це - …Яка фігура називається кулею?Яка січна площина має найбільшу площу?Яким є взаємне розміщення дотичної до кулі площини і радіусом кулі, проведеним в точку дотику?Як називається відрізок, який сполучає дві точки кульової поверхні і проходить через центр?Як називається частина кулі, яку відтинає від неї січна площина?Вправа «Питання-відповідь»

НІ ТАКТАКНІ НІ Гра «Вірю – не вірю»1. Існує конус у якого висота більша від твірної2. Існує конус осьовим перерізом якого є правильний трикутник3. Якщо висоту циліндра збільшити в 2 рази, то площа бічної поверхні збільшиться в 2 рази4. Якщо радіус циліндра зменшити в 4 рази, то площа основи зменшиться в 4 рази5. Радіус будь-якого перерізу сфери площиною менший від радіуса сфери

1. Множина всіх точок простору, віддалених від поданої точки на відстань, що не перевищує задану називають сферою 2. Переріз конуса площиною, яка проходить через його вершину і хорду, є прямокутний трикутник.3. Циліндр утворюється в результаті обертання паралелограма навколо однієї із сторін 4. Циліндр називається прямим, якщо його твірні паралельні до площини основи.5. Конус утворюється в результаті обертання прямокутного трикутника навколо гіпотенузи6. Малим колом називають переріз сфери діаметральною площиною. Вправа «Знайди помилку»

Довжина кола…Площа квадрата з стороною 2𝜋Площа круга…Довжина півкола…Подвоєна площа круга… А) 4𝜋2 Б) 2𝜋𝑅В) 𝜋𝑅2 Г) 2𝜋𝑅2 Д) Інша відповідь R{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}АБВГД1.2.3.4.5. Вправа «Установи відповідні пари»

S п.п. цил = 2𝜋 Н (R + H) Vцил = S біч  ∙ R = 𝜋R2 Rосн. HHSп.п. кон = πR (R + Н)Vкон = Sосн H = πR2 HL13 13 Vкул = 4 πR243 3 Sпов.сф = 4 πR2 Rh. Вправа «Вірус»

10 На рисунках зображено фрагменти розгорток циліндра і конуса. Знайдіть площу повної поверхні даних фігур.12𝜋 618𝜋 Sп= 2 Sосн + Sбіч = 72π + 120π = 192πSп= Sосн + Sбіч = 81π + 54π = 135πЗНОSoсн = πR22 πR = 12𝝅 R = 6 Socн = π62 = 36 πSбіч = 2πRH2 πR H2 πR 𝒍 Soсн = πR22 πR = 1𝟖𝝅 R = 9 Socн = π92 = 81 πSбіч = πR𝒍 Sбіч = 2π6∙10 = 120 π  Sбіч = π9∙6 = 54 π  

ЗНО

Обчислити розхід матеріалів та їхню вартість для монтажу каркасу зерносховища з оцинкованого металу. Математичне моделювання

СХЕМАТИЧНЕ КРЕСЛЕННЯ ВИРОБУ720670580040050

Sб=2πRHSp = 2πR(Н + R)Площа поверхні циліндра

S = π r (r + l)Sб = π r l. Площа поверхні конуса

Sб=π l (R+r)Sп=π l (R+r)+ π R2+π r2 Площа поверхні зрізаного конуса

СХЕМАТИЧНЕ КРЕСЛЕННЯ ВИРОБУ720670580040050

1 Обчислити площу бічної поверхні циліндра висотою 580 см та діаметром 400 см. Постановка задачіSб=2πRH

2 Обчислити площу бічної поверхні конуса висотою 50 см та діаметром 50 см Постановка задачіSб = π r l

3 Обчислити площу бічної поверхні зрізаного конуса висотою 90 см, діаметрами основ 400см та 50 см Постановка задачіSб=π l (R+r)

1 Обчислити площу бічної поверхні циліндра висотою 580 см та діаметром 400 см. Розв’язок задачіSб=2πRHH = 580 см = 5,8 м. R = 𝑑2 = 200 см = 2 м Sб= 2π·2·5,8 = 23,2π ≈72,85 (м2)

2 Обчислити площу бічної поверхні конуса висотою 50 см та діаметром 50 см Розв’язок задачіSб = π r lr = 𝑑2 = 25 см = 0,25 м H = 50 см = 0,5 м𝑙= 𝐻2+𝑟2 𝑙= 0,52+0,252 =  0,25+0,0625 = 0,3125 =0,56 𝑆б= 𝜋∙0,25∙0,56 = 0,14 𝜋 ≈ 0,44 (м2) 

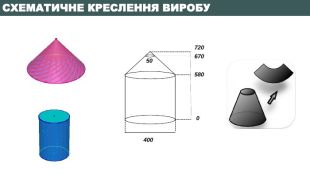
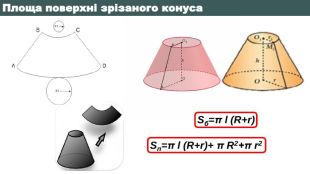
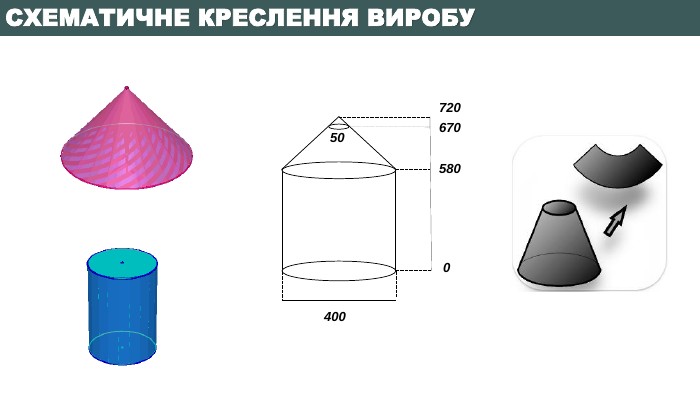
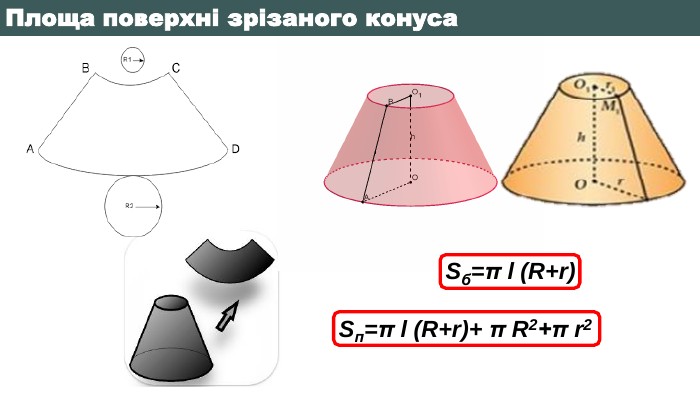
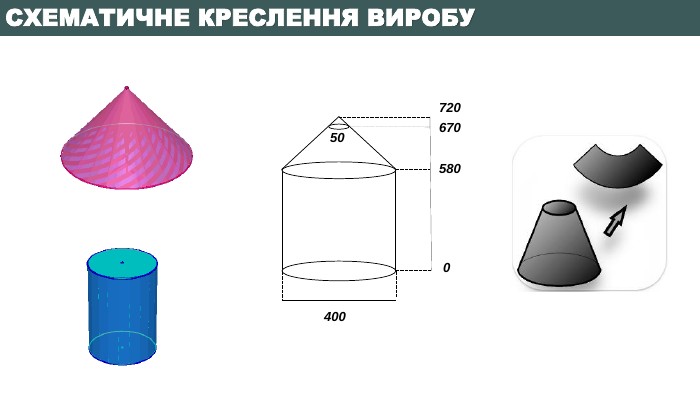
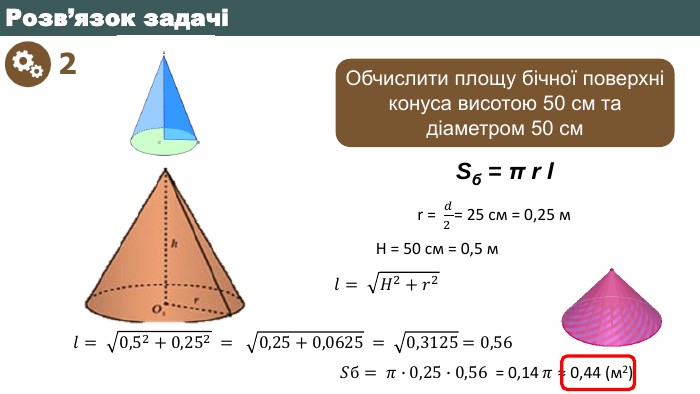
3 Обчислити площу бічної поверхні зрізаного конуса висотою 90 см, діаметрами основ 400см та 50 см Розв’язок задачіSб=π l (R+r)R = 𝑑2 = 200 см = 2 м r = 𝑑2 = 25 см = 0,25 м H = 90 см = 0,9 м 𝑙= 𝐻2+(𝑅−𝑟)2𝑙= 0,92+(2−0,25)2 =  0,81+(1,75)2 =  0,81+3,0625 = 3,8725 ≈ 1,97 𝑆б= 𝜋∙1,97 2+0,25= 4,43 π ≈ 13,92 (м2) 

Обчислити повну площу каркасу зерносховища Розв’язок задачіSб = 72,85 + 13,92 + 0,44 = 87,21 (м2)720670580040050

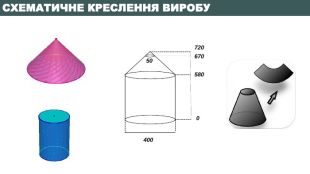
Бажаю творчих успіхів!01.11.2022 Домашнє завдання. Знайти необхідну кількість листів оцинкованого металу товщиною 3 мм, враховуючи найраціональніший спосіб розкрою матеріалу та її вартість за найвигіднішими цінами в інтернет пропозиціях. Виясніть: можливо вигідніше виготовити ємність такого ж об’єму у формі прямокутного паралелепіпеда з діагоналлю квадрата в основі, що дорівнює основі циліндра і дахом у вигляді чотирикутної піраміди. Повторити опорний конспект та основні формули з теми «Тіла обертання»

Скільки у зв'язці електродів для електрозварювання, якщо їх загальна маса 10 кг, а кожний електрод, це шматок сталевого дроту довжиною 45см і діаметром 6 мм. Густина сталі 7600 кг/м3 Розв’яжіть задачу

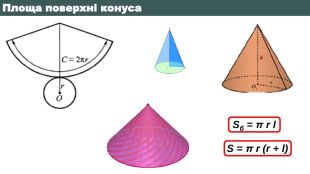
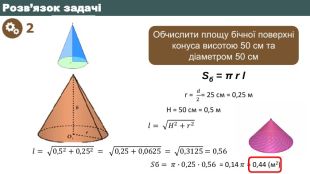
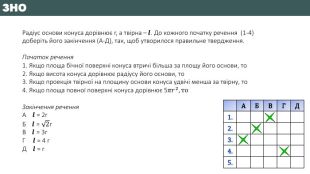
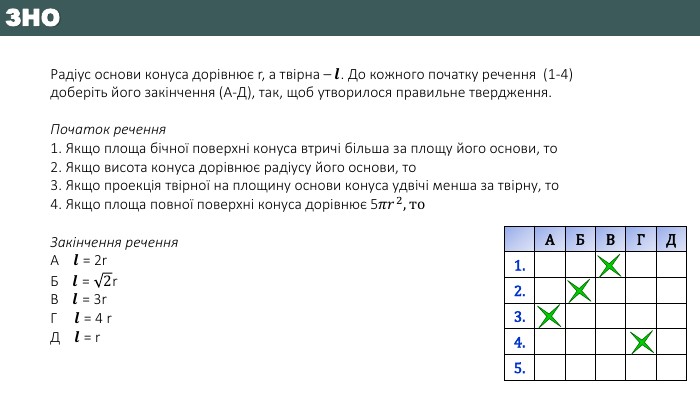
Радіус основи конуса дорівнює r, а твірна – 𝒍. До кожного початку речення (1-4) доберіть його закінчення (А-Д), так, щоб утворилося правильне твердження. Початок речення1. Якщо площа бічної поверхні конуса втричі більша за площу його основи, то2. Якщо висота конуса дорівнює радіусу його основи, то3. Якщо проекція твірної на площину основи конуса удвічі менша за твірну, то4. Якщо площа повної поверхні конуса дорівнює 5𝜋𝑟2, то. Закінчення речення. А 𝒍 = 2r. Б 𝒍 = 2r. В 𝒍 = 3r. Г    𝒍 = 4 r. Д 𝒍 = r {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}АБВГД1.2.3.4.5. ЗНО

Скільки потрібно фарби (у кг), щоб пофарбувати трубу діаметром 20 см і довжиною 8 м, якщо на 1 м2 витрачається 0,25 кг фарби? Розв’язання: ЗНО

Скільки потрібно скла (у м2) для виготовлення акваріуму, який має форму сфери, радіусом 15 см, якщо площа кульового сегменту (кришка акваріуму) дорівнює 40πсм2? Розв’язання: ЗНО

Скільки морозива «ріжок», радіусом 2 см і висотою 8 см можна виготовити із вафельного листа, який має форму прямокутника розміром 50 х 80 см?Розв’язання: ЗНО

Визначити масу купи зерна, яка має форму конуса з довжиною основи 31,4м і твірною 6м. Маса 1м зерна складає 690кг. ЗНО

Соснова колода має діаметри кінців 42 см і 25 см, а довжину 15,5 м. Яку помилку (у відсотках) роблять, обчислюючи об’єм колоди множенням площі його середнього поперечного перерізу на довжину (висоту) колоди?ЗНО

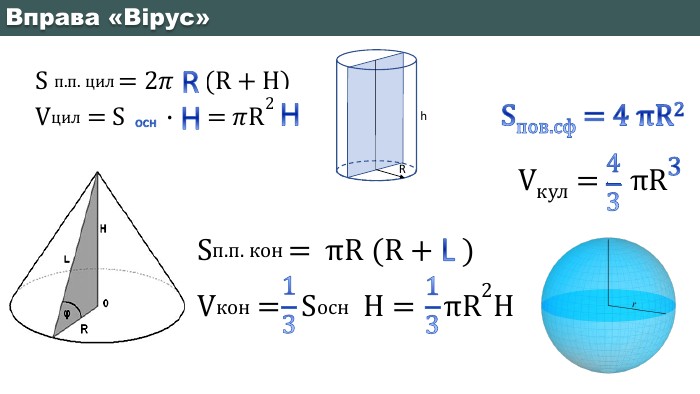
ОБ’ЄМИ ТІЛ ОБЕРТАННЯфІгураформулаправило. Циліндр V=S*HОб’єм циліндра дорівнює добутку площі основи на висоту. Конус V=1/3*S*HОб’єм конуса дорівнює третині добутку площі основи на висоту. Зрізаний конус. Об’єм зрізаного конуса Куля Об’єм кулі радіуса R дорівнює . Кульовий сегмент. Об’єм кульового сегмента. Кульовий сектор. V=2/3*П*R2*НОб’єм кульового сектора.43𝜋𝑅3