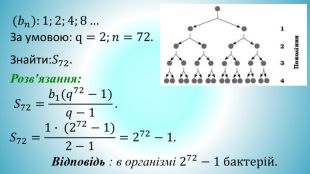
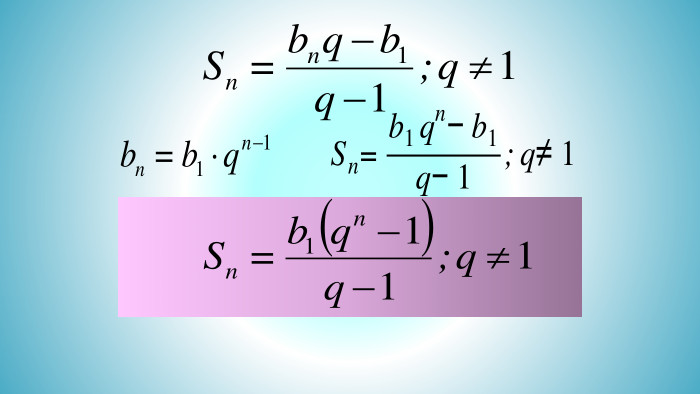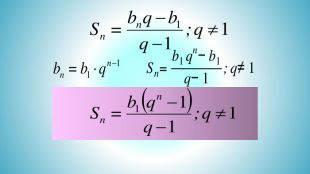Презентація "Формула суми геометричної прогресії"
Про матеріал
Презентація "Формула суми геометричної прогресії" допоможе вчителю математики в доступній формі почснит и учням дану тему Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку