Презентація "Функція" 7 клас










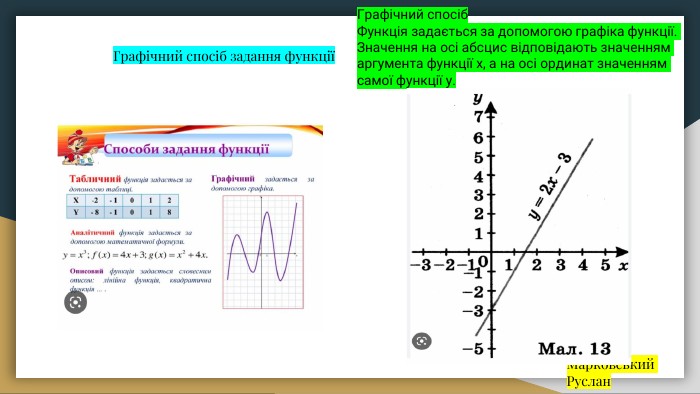


![Область визначення і область значень функціїГулий Єгор. Область визначення (старіший термін — область задавання[джерело?]) — множина допустимих значень аргументу функції. Позначатиметься як D(y), якщо вказується область визначення функції y=f(x). Значення змінних, на яких задається функція �=�(�), називають допустимими значеннями змінних. Область значення – це множина усіх значень, яких набуває функція, тобто значень змінної Y. Позначається E(y). Гулий Єгор Область визначення і область значень функціїГулий Єгор. Область визначення (старіший термін — область задавання[джерело?]) — множина допустимих значень аргументу функції. Позначатиметься як D(y), якщо вказується область визначення функції y=f(x). Значення змінних, на яких задається функція �=�(�), називають допустимими значеннями змінних. Область значення – це множина усіх значень, яких набуває функція, тобто значень змінної Y. Позначається E(y). Гулий Єгор](/uploads/files/646761/349682/401691_images/14.jpg)



Мета Проектупоглибити та систематизувати знання учнів функцію;формувати обчислювальні навички учнів, розвивати самостійність мислення, вчити об’єктивно оцінювати себе і коригувати свою діяльність та інших учнів в ході виконання проректу;формувати в учнів вміння здійснювати вибір навчально – пізнавального завдання; вміння осмислювати й використовувати інформацію з різних джерел; вміння співпрацювати в групах, проявляти ініціативу; робити висновки;виробити у школярів практичні навички під час побудови графіків функції;виховувати спостережливість, науковий підхід , та любов до математики.
Опис проекту. Проект пропонується для реалізації з учнями 7 класу під час вивчення теми «Функція». Даний проект об’єднує математику та інші дисципліни. У сьомому класі вводиться одне з фундаментальних математичних понять – поняття функції. Тут же розглядається лінійна функція та її графік. Згодом ці відомості використовуються для графічної ілюстрації розв‘язування лінійного рівняння з однією змінною, а також системи двох лінійних рівнянь з двома змінними. Інші види функцій розглядаються у 8 – 11 класах. Клас збирає інформацію, підбирає цікаві факти, готує коротку презентацію за змістом опрацьованого матеріалу, робить висновки.
Анотація. Під час роботи над проектом, учні повинні не тільки навчитися збирати первинну інформацію познайомляться поняттям «функція», навчаться знаходити область визначення та область значень функції. Удосконалять та поглиблять свої знання із теми. Виявлять зв'язок математики з іншими науками. Відкривають для себе багато нового, цікавого захоплюючого з історії математики. Навчаться захищати свій проект перед однокласниками, критично мислити , розмірковувати, робити висновки, приймати самостійні рішення.
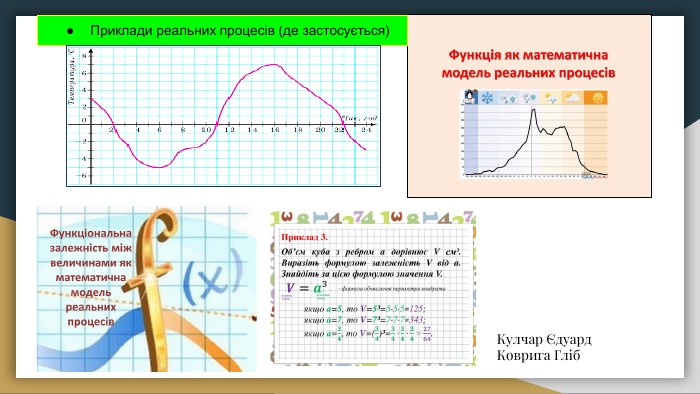
Задачі з функцією або якісь завдання. Приклад номер 1 Нехай сторона квадрата дорівнює А см, а його периметр дорівнює Р см. Для кожного завдання змінної А можна знайти відповідне значення змінної Р. НАПРИКЛАД: Якщо а=2, то Р=4•2=8; Якщо а=5, то Р=4•5=20;Якщо а=1,2, то Р =4•1,2=4,8. Приклад номер 2 Нехай дно функцію у=6/х+3,де-2≤х≤3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю.{9 E99808 B-2 C6 A-4 EB8-B8 FF-6544 FFCA0 D54} Х-2-10123 У6321,51,21 КОЗЮПА ДАНІІЛ Позначимо на кординатній площині точки(х,у), координати яких подано в таблиці, тобто точки (-2,6) (-1,3) (0,2) (1,1,5) (2,2,5) (3,1). ДЯКУЮ ЗА УВАГУ!!!
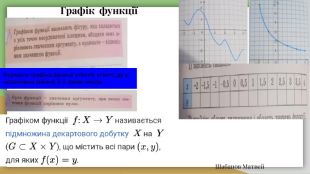
Гусаков Матвій. Хто ввів термін “ функція” ? (історичний екскурс в історію)Термін «функція» вперше ввів Г. Лейбніц. Озн. Функцією називається відповідність, при якій елементу х із множини D відповідає деякий певний елемент y із множини E. D – область визначення функції (позн. D(f));Е – область значень функції (позн. E(f)). Якщо D(f) і E(f) – числові множини, то функція називається числовою. Числовою функцією з областю визначення D називається відповідність, при якій кожному числу х Î D відповідає деяке цілком означене число y.(М. Лобачевського і Л. Діріхле) Якщо кожному числу х з деякої числової множини Х за певним правилом поставлене у відповідність єдине число y, то кажуть, що у є функція від х.
Прохорова Андріана. Функція — це така залежність, при якій кожному значенню х з деякої множини відповідає єдине значення змінної у. Записують це: y=f(x). Змінну y називають функцією від x, чи залежною змінною. Функція y=f(x) є зростаючою, якщо більшому значенню аргументу відповідає більше значення функції. Означення ФункціїФункція y=f(x) є спадною, якщо більшому значенню аргументу відповідає менше значення функції. Термін "функція" вперше запропонував у 1692 р. видатний німецький філософ математик Готфрід Вільгельм Лейбіц (1646 – 1716) для характеристики різних відрізків, що сполучають точки деякої кривої.
Крючко Олександра. Уявлення про залежність між двома величинами(хто така х і у)Х-це правило, яке кожному елементу з першої множини — області визначення ставить у відповідність елемент з іншої множини — області значень. Часто цю другу множину називають цільовою множиною чи образом функції чи відображення.ЇїЗале́жна змі́нна —У математичному моделюванні — змінна, яка розраховується за модельним рівнянням або відповідними правилами з використанням незалежних змінних
Область визначення і область значень функціїГулий Єгор. Область визначення (старіший термін — область задавання[джерело?]) — множина допустимих значень аргументу функції. Позначатиметься як D(y), якщо вказується область визначення функції y=f(x). Значення змінних, на яких задається функція �=�(�), називають допустимими значеннями змінних. Область значення – це множина усіх значень, яких набуває функція, тобто значень змінної Y. Позначається E(y). Гулий Єгор
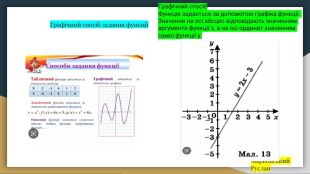
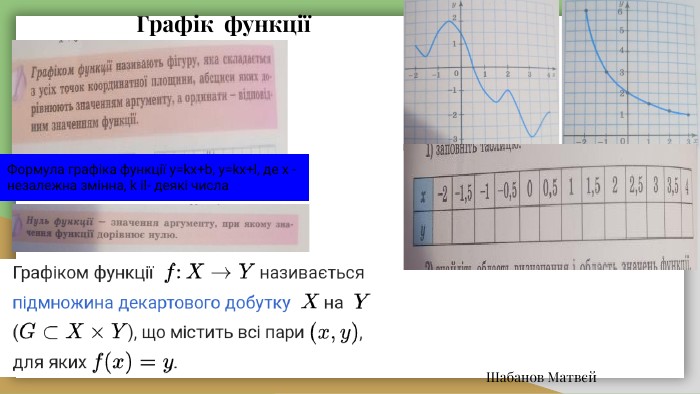
Лінійна функція. Котолуп Ольга. Лінійна функція — це функція, яку можна задати формулоюy=kx+b,де X - незалежна змінна,а K і B - деякі числа. Графіком лінійної функції y=kx+b є пряма. Щоб побудувати графік даної функції, нам достатньо мати координати двох точок, що належать графіку функції. Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції. У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає. Якщо k>0,тоді лінійна функція y=kx+bзростає;якщо k<0,тоді лінійна функція y=kx+b спадає.
Яшний Назар Аналітичний спосіб завдання функцій полягає в тому ,що увиражають через х задопомогою формули або аналітичного виразу . Завдання функцій формулою зручне тим. Що дає можливість знаходити значення функції для довільного значення аргументу. Аналітичний спосіб задання функції Дякую За увагу Удачі в навчанні


про публікацію авторської розробки
Додати розробку