Презентація "Геометричні переміщення"
Про матеріал
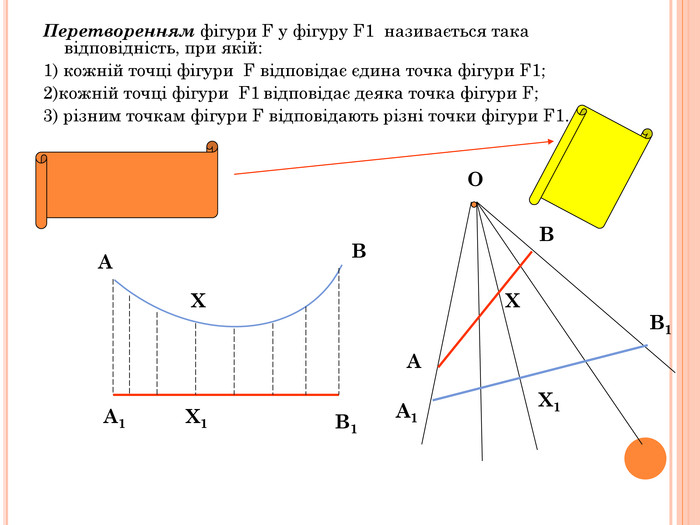
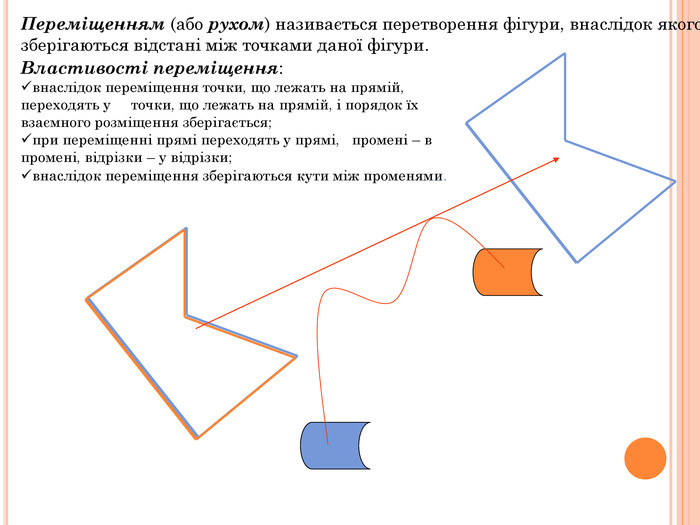
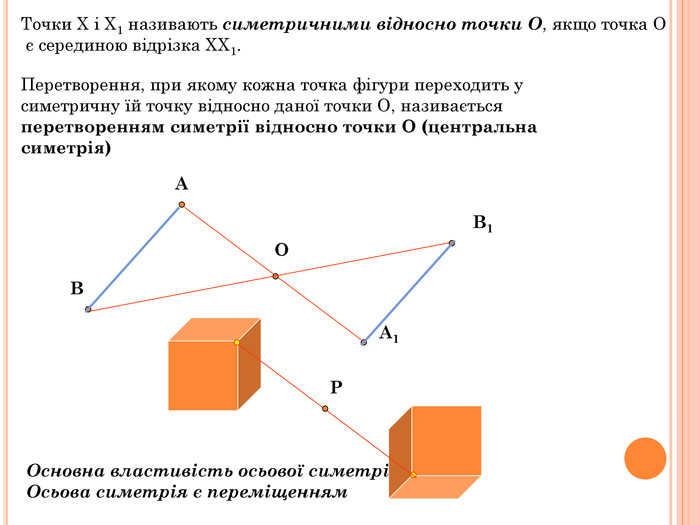
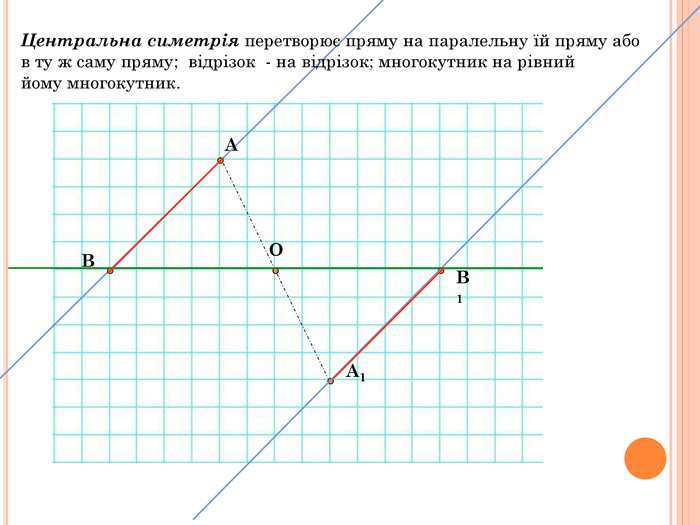
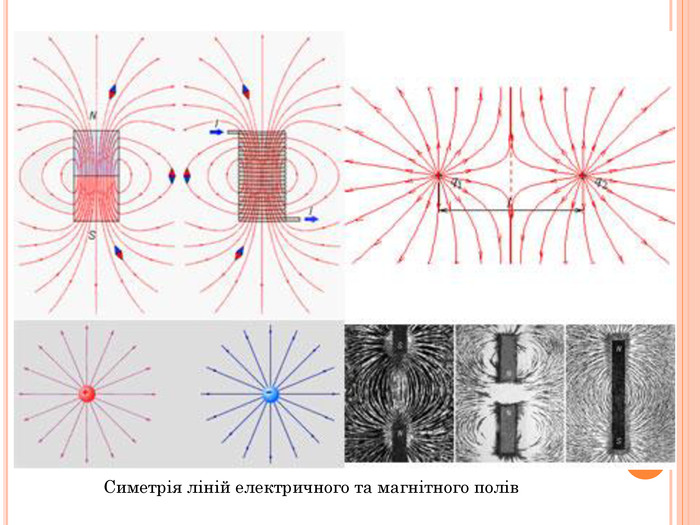
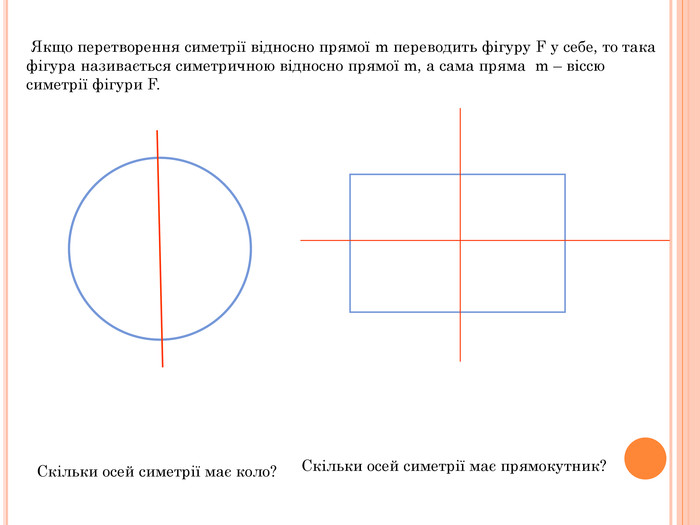
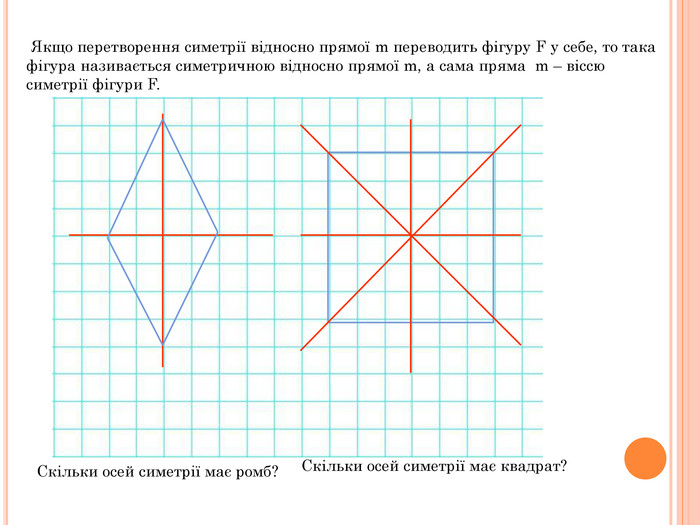
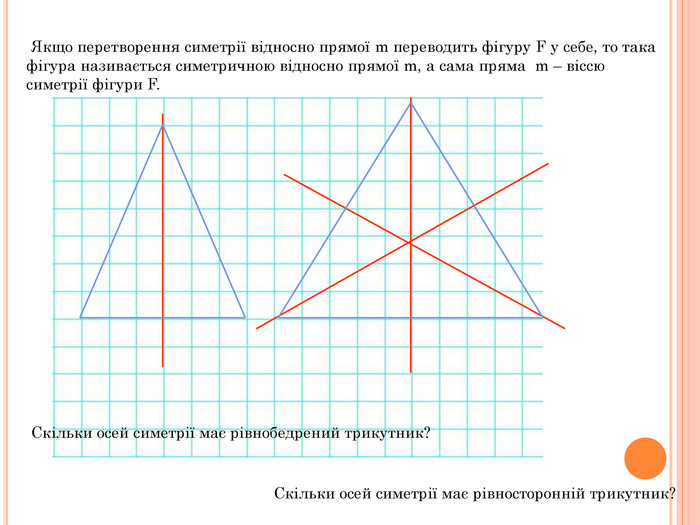
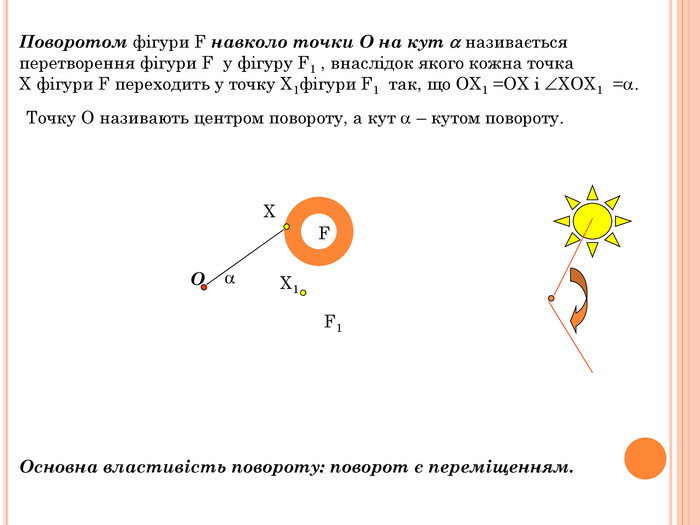
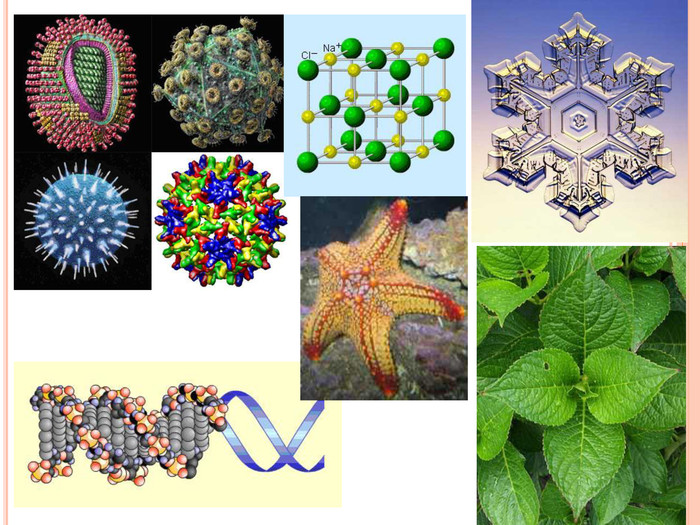
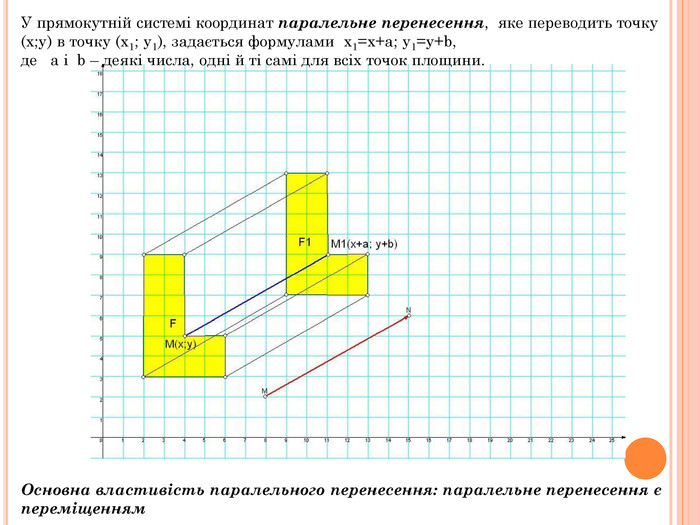
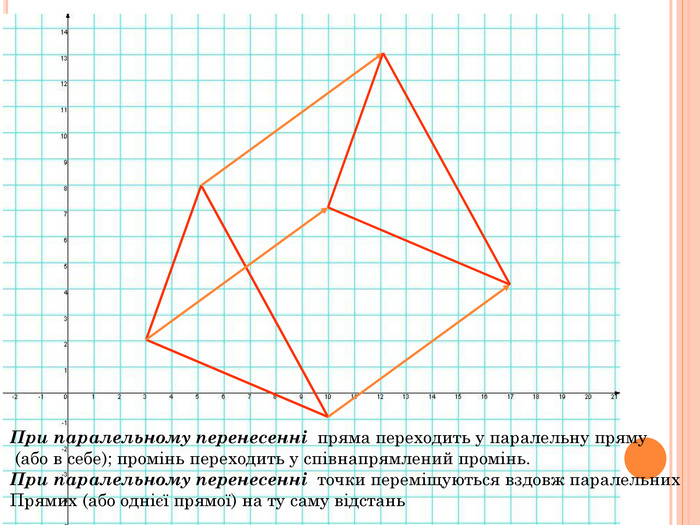
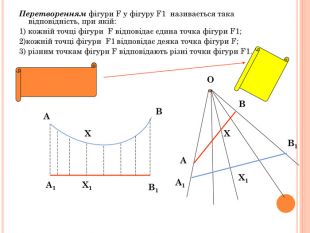
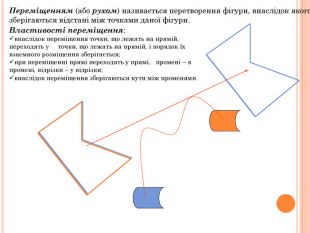
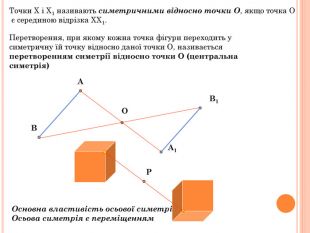
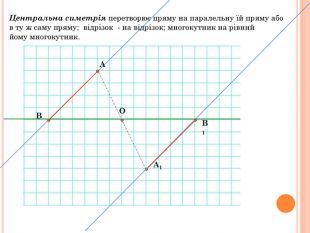
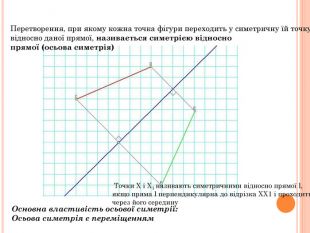
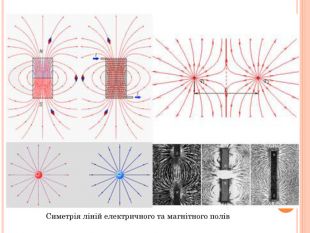
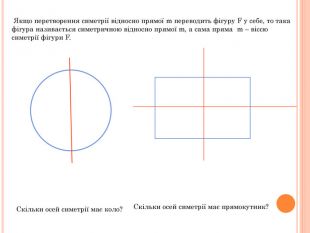
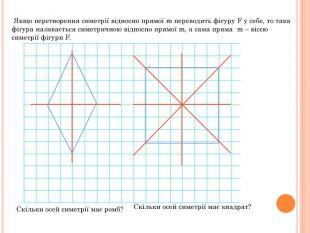
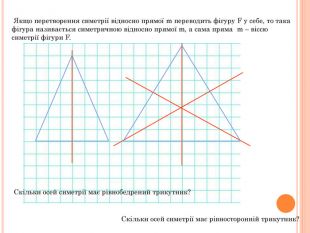
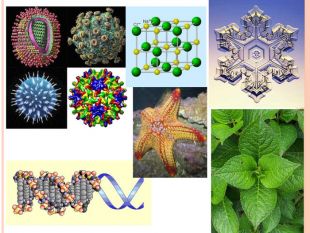
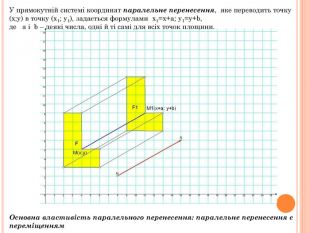
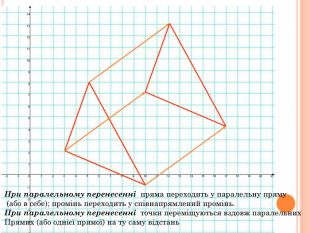
Презентація містить основну теоретичну інформацію про геометричні переміщення: симетрію, поворот та паралельне перенесення, а також де ці види переміщень зустрічаються у побуті Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку