Презентація Геометрія 7 клас "Суміжні та вертикальні кути. Ознаки та властивості паралельних прямих"

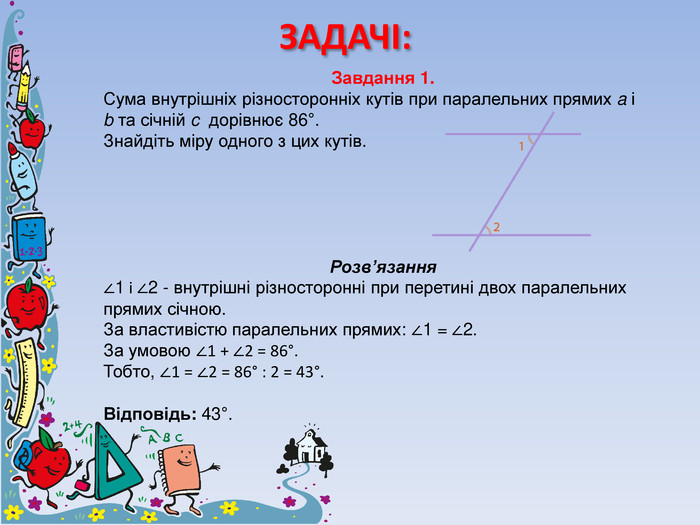
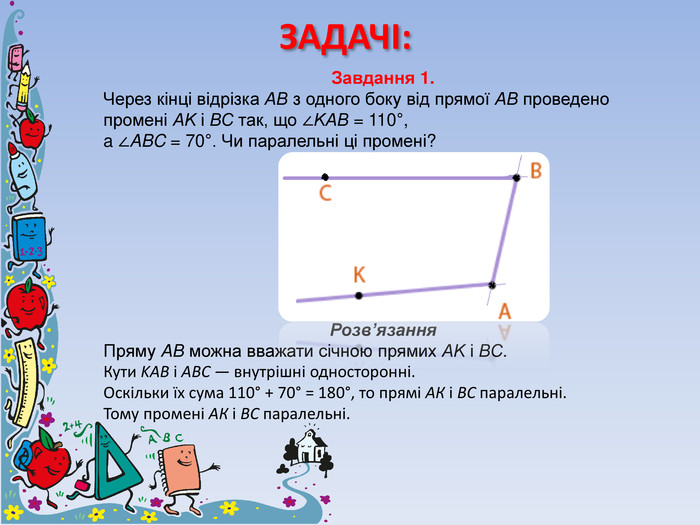
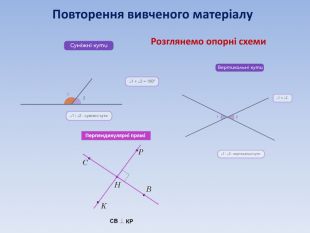
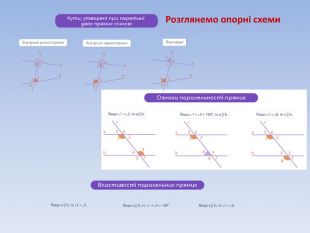
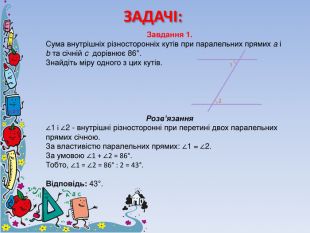
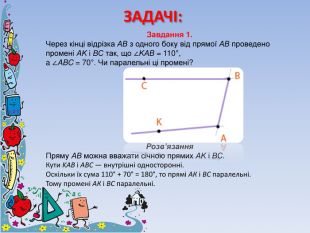
Повторення і систематизація навчального матеріалу7 клас. ГЕОМЕТРІЯСуміжні та вертикальні кути. Ознаки та властивості паралельних прямих

ПРОСМОТР ПРЕЗЕНТАЦІЇ

Розглянемо відеоурокhttps://api.gioschool.com/api/v1/file/stream/67757b5a-ac50-4500-a77d-392f9319eef9

Повторення вивченого матеріалу. Розглянемо опорні схеми

ЗАДАЧІ: Завдання 1. Знайдіть міри суміжних кутів, якщо один з них на 50° більший, ніж другий. Розв’язання. Нехай міра меншого із суміжних кутів дорівнює х, тоді міра більшого кута х + 50°. За властивістю суміжних кутів х + х + 50° = 180°, звідки х = 65°, х + 50° = 115°.  Відповідь: 65° і 115°.

ЗАДАЧІ: Завдання 2. Один із чотирьох кутів, які утворилися при перетині двох прямих, удвічі більший від другого. Знайдіть міру кожного з утворених кутів. Розв’язання. При перетині двох прямих утворюються вертикальні і суміжні кути. Оскільки вертикальні кути рівні, то вони умову задачі не задовольняють. Робимо висновок: один із суміжних кутів удвічі більший від другого, їх міри х і 2х. За властивістю суміжних кутів х + 2х = 180°, х = 60°, 2х = 120°. Відповідні їм вертикальні кути також дорівнюють 60° і 120°. Відповідь: 60°, 120°, 60°, 120°.

Повторення вивченого матеріалу. Розглянемо відеоурокhttps://api.gioschool.com/api/v1/file/stream/e22879ac-ba57-4057-9db8-a89e9399ac3f

Розглянемо опорні схеми

ЗАДАЧІ: Завдання 1. Сума внутрішніх різносторонніх кутів при паралельних прямих a і b та січній c дорівнює 86°. Знайдіть міру одного з цих кутів. Розв’язання∠1 і ∠2 - внутрішні різносторонні при перетині двох паралельних прямих січною. За властивістю паралельних прямих: ∠1 = ∠2. За умовою ∠1 + ∠2 = 86°. Тобто, ∠1 = ∠2 = 86° : 2 = 43°. Відповідь: 43°.

ЗАДАЧІ: Завдання 1. Через кінці відрізка АВ з одного боку від прямої АВ проведено промені АK і ВС так, що ∠KАВ = 110°, a ∠ABC = 70°. Чи паралельні ці промені? Розв’язання. Пряму АВ можна вважати січною прямих АK і ВС. Кути KАВ і ABC — внутрішні односторонні. Оскільки їх сума 110° + 70° = 180°, то прямі АК і ВС паралельні. Тому промені АК і ВС паралельні. 

Дякую за урок!