Підготовка до контрольної роботи з теми: «Взаємне розміщення прямих на площині»

Початковий рівень (3 бали)

У завданнях 1-3 виберіть правильну відповідь.

1.    Один із суміжних кутів дорівнює 60°. Чому дорівнює інший?

       А)    100°;       Б)   70°;       В)   120°; Г)   35°.

Розв’язання:

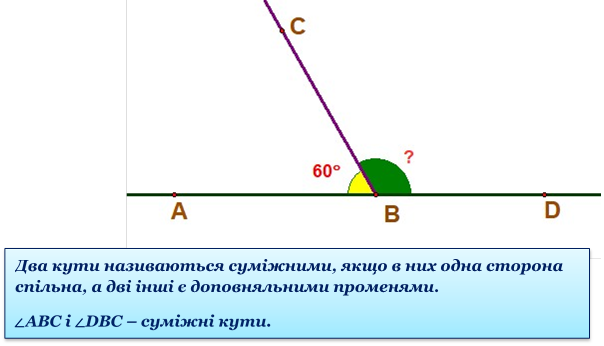
60° +DBC = 180°;

DBC = 180° - 60°;

DBC = 120°.

Відповідь: В)

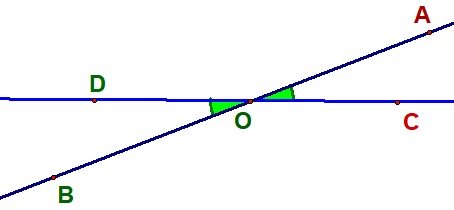
2.    Знайдіть вертикальні кути, якщо їх сума дорівнює 50°

       А)    100°;      Б)   25°;       В)   50°;      Г)   65°.

Розв’язання:

 

 

 

 

 

 

Два кути називають вертикальними, якщо сторони одного   кута є доповняльними променями сторін другого.

 ∠BOD i ∠AOC, ∠AOD i ∠BOC – вертикальні кути

 

∠BOD = 50° : 2; ∠BOD = 25°.

Відповідь: Б)

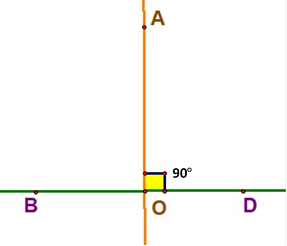
3.    Як називаються прямі, які перетинаються під прямим кутом?

А) паралельні;                          Б) вертикальні; 

В) перпендикулярні;                Г) суміжні.

 

Розв’язання:

 

 

 

 

 

Відповідь: B)

Середній рівень (3 бали)

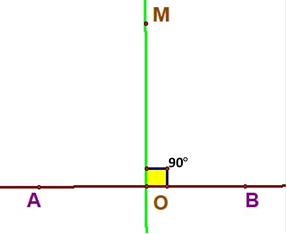
4.                Скільки перпендикулярних прямих можна провести до даної прямої через точку, що не лежить на ній?

 

Розв’язання:

 

5.                Дві прямі перетинаються. Один з отриманих кутів дорівнює 35°. Знайдіть градусну міру інших кутів.

Розв’язання:

 

 

 

 

 

  За  означенням AOC i BOD – вертикальні кути. За властивістю вертикальних кутів AOC = BOD. Отже AOC = 35°. 

 За означенням BOD і AOD – суміжні кути. За властивістю суміжних кутів:

 BOD + AOD = 180°;  35° + AOD = 180°; 

AOD = 180° - 35°;

AOD = 145°.

Так як AOD і ВОС – вертикальні кути, то ВОС = 145°.

Відповідь: 145°; 35°; 145°

6. Один із суміжних кутів на 20° більший від другого. Знайдіть ці кути. .

Розв’язання:

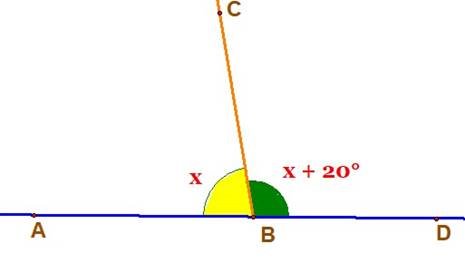
За означенням АВС і DBC – суміжні кути. 

Нехай АВС = х градусів, тоді DBC = (х + 20°) градусів. За властивістю суміжних кутів:

АВС + DBC = 180°;

х + х + 20° = 180°; 2х + 20° = 180°;

2х = 180° - 20°;

2х = 160°; 

х = 160° : 2; х = 80° - градусна міра АВС

80° + 20° = 100° - градусна міра DBC.

Відповідь: 80°; 100°

Достатній рівень (3 бали)  

7. Два суміжні кути відносяться, як 2 : 7. Знайдіть ці кути. 

Розв’язання:

 

 

 

 

 

 

 

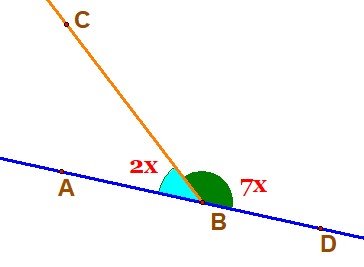
І спосіб

Розділимо розгорнутий кут ABD на 9 (2+7) рівних частин. Градусна міра розгорнутого кута дорівнює 180°. Одна частина становить – (180° : 9 = 20°) градусів. Маємо АВС = 2·20° = 40°, CBD = 7·20° = 140°. 

ІІ спосіб

Нехай коефіцієнт пропорційності – х. Тоді градусна міра  АВС = 2х градусів, а CBD = 7х градусів. Сума суміжних кутів 180°. Маємо рівняння:

2х + 7х = 180°; 9х = 180°; х = 180° : 9; х = 20° 

2·20° = 40° - АВС;  180°- 40° = 140° - CBD Відповідь: 40°; 140°

8. Дві прямі перетинаються. Чому дорівнюють утворені кути, якщо сума двох з них становить 242⁰

Розв’язання:

 

Проаналізуємо задачу.

 Сума суміжних кутів дорівнює 180°, тому 242° - це сума вертикальних

кутів. За властивістю вертикальні кути рівні. Тому                                  MON = POR = 242° : 2 = 121°.

POM i MON – суміжні кути, сума яких дорівнює 180° (за властивістю). Отже POM = 180° - 121° = 59°. 

POM i NOR – вертикальні кути . POM = NOR = 59° (за властивістю).

Відповідь: 121°; 59°; 121°; 59°

Високий рівень (3 бали)  

9.  Через точку перетину двох прямих на площині проведено промінь, перпендикулярний до однієї з прямих. Знайдіть кути, утворені при перетині цих прямих, якщо даний промінь з другою прямою утворює кут 38⁰.

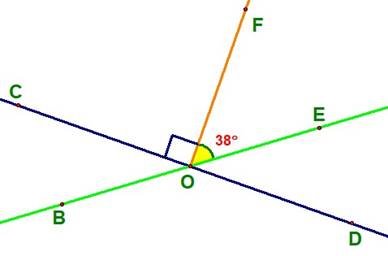Розв’язання:

 

 

 

 

 

 

За властивістю величини кута СОЕ = СOF + FOE : СОЕ = 90° + 38° =

128°.  СОЕ і BOD – вертикальні кути, тому за властивістю вертикальних кутів СОЕ = BOD = 128°.

СОЕ суміжний з EOD, отже EOD = 180° - 128° = 52°. EOD = ВОС = 52° як вертикальні кути.

Відповідь: 128°; 52°; 128°; 52°