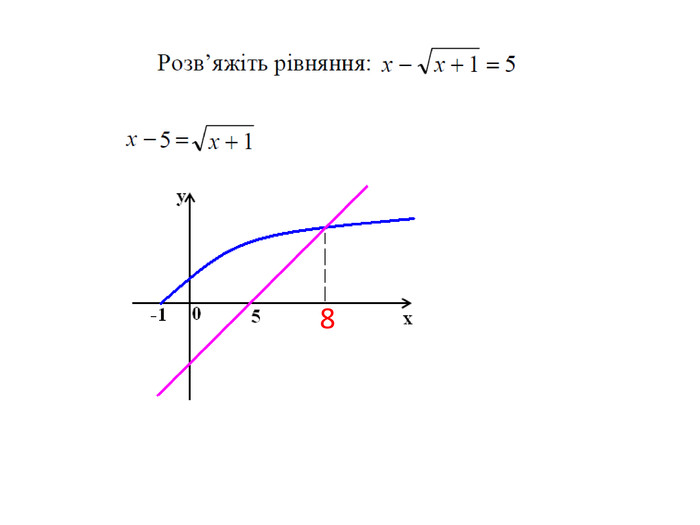
презентація "Ірраціональні рівняння"
Про матеріал
Презентація містить основні типи ірраціональних рівнянь. Всі завдання можуть розглядатись в плані підготовки до ЗНО. Рівень складності відповідає ІІ частині (завдання з відповіддю у вигляді числа). Для рівнянь, де існує декілька коренів, можна ставити питання у вигляді: "Записати суму або добуток коренів" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку