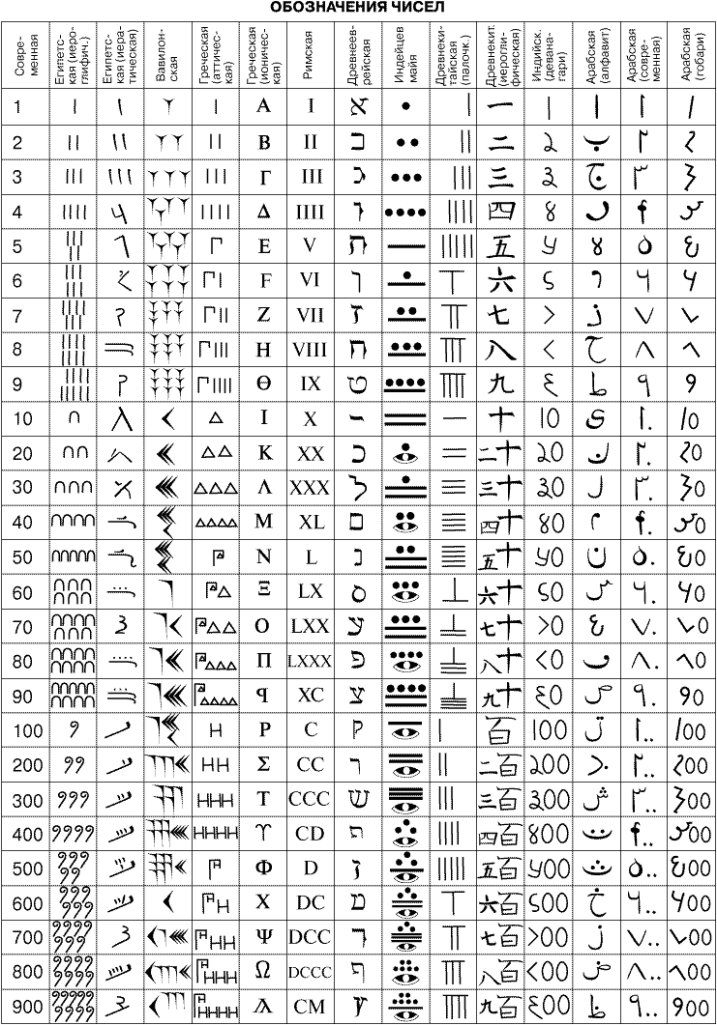
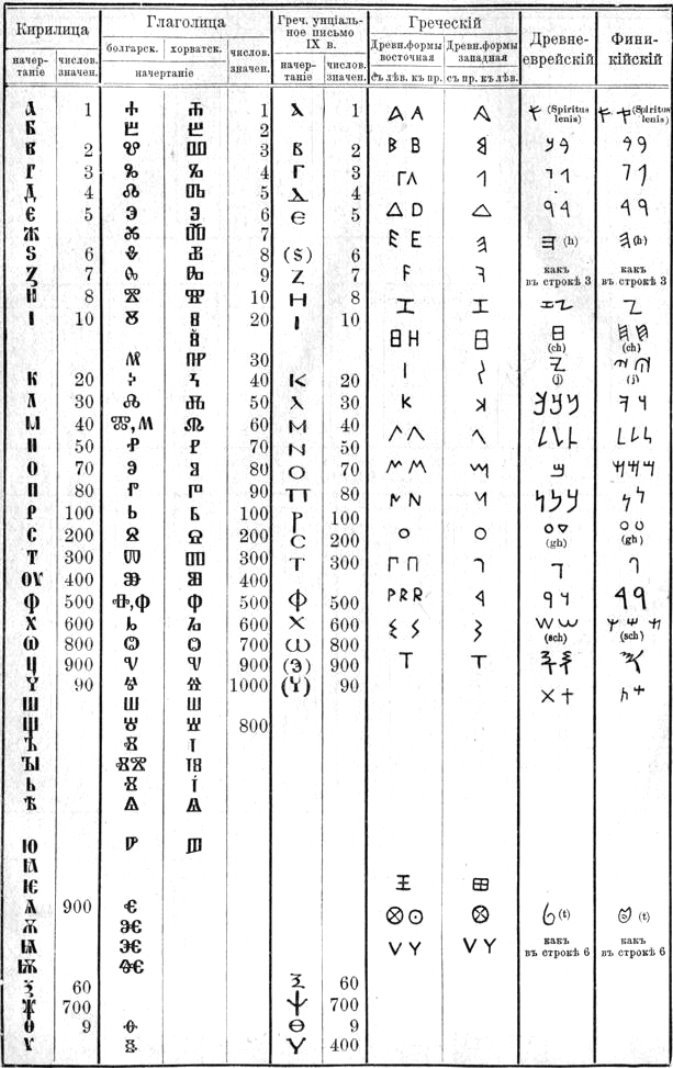
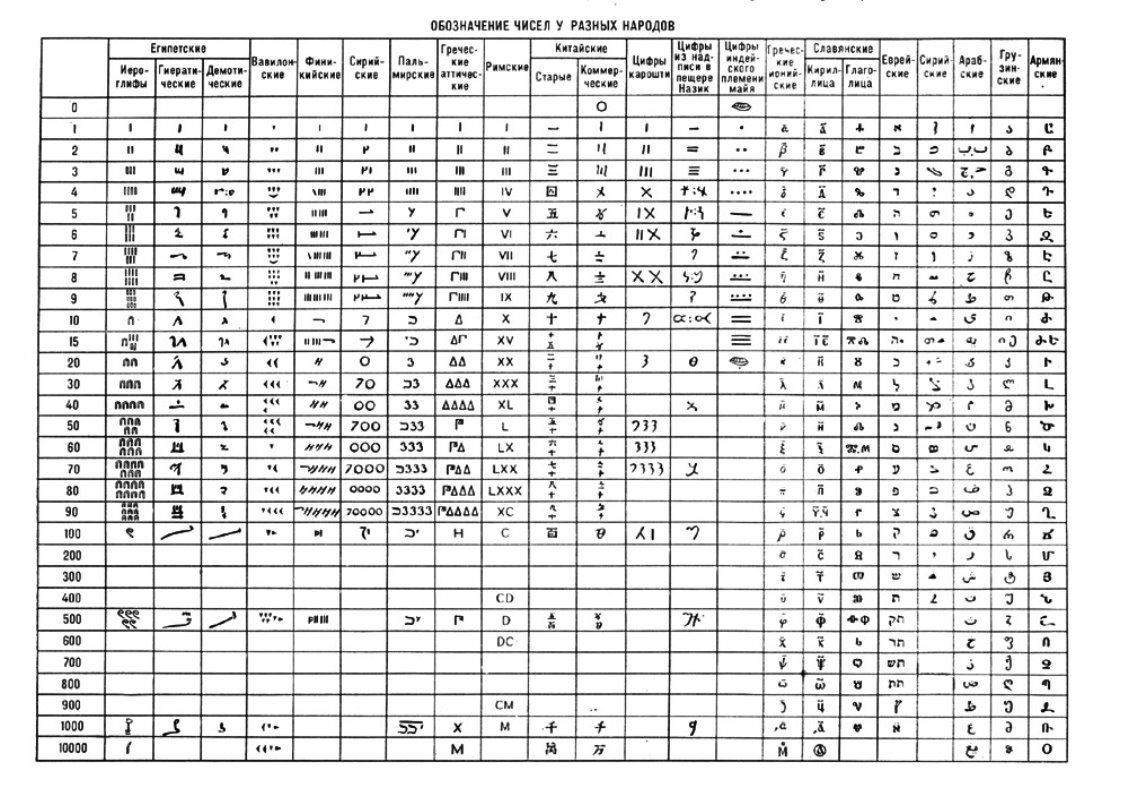
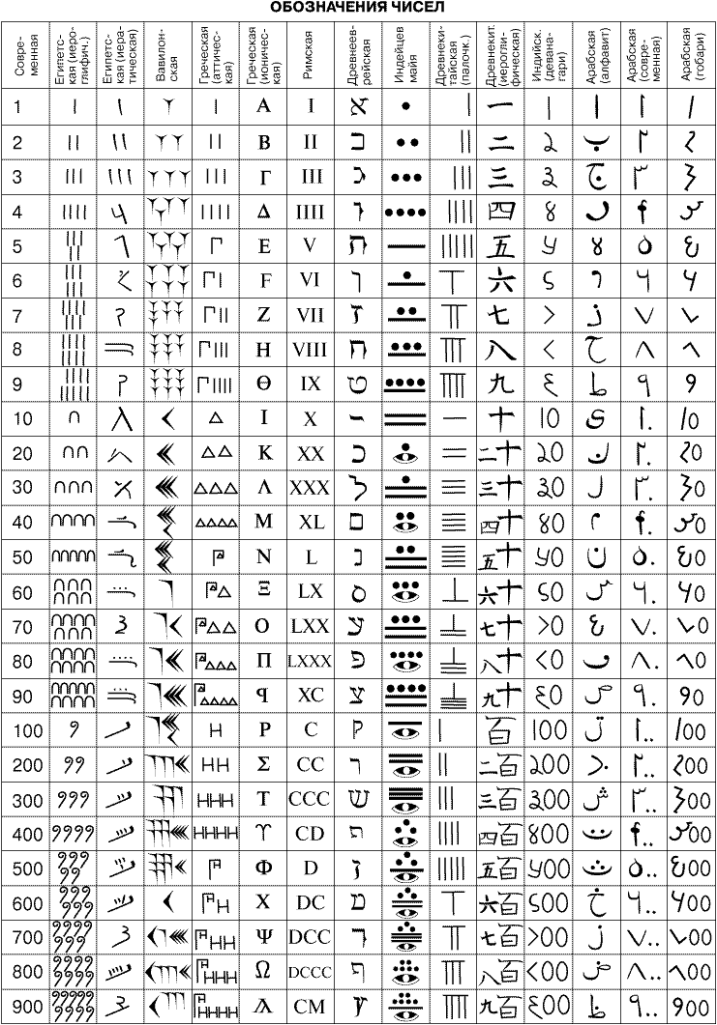
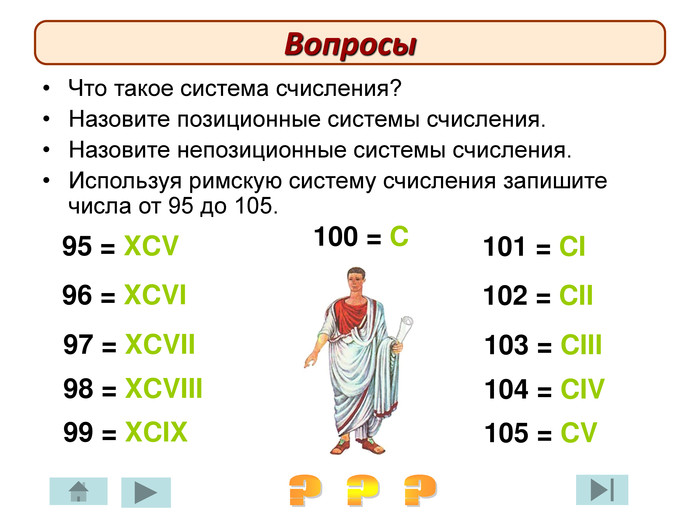
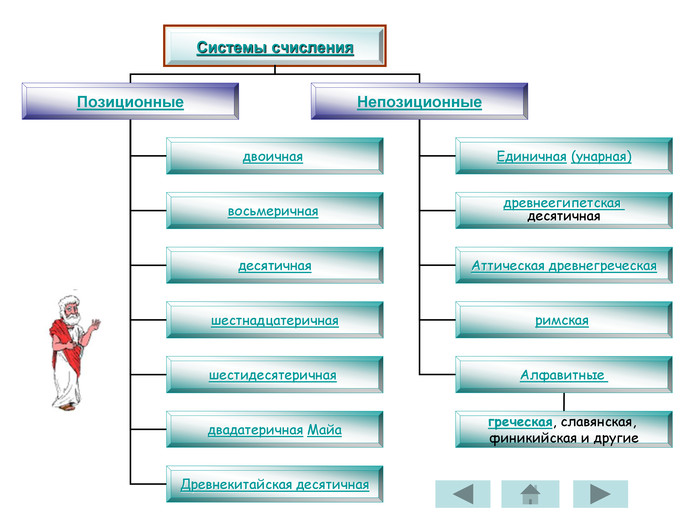
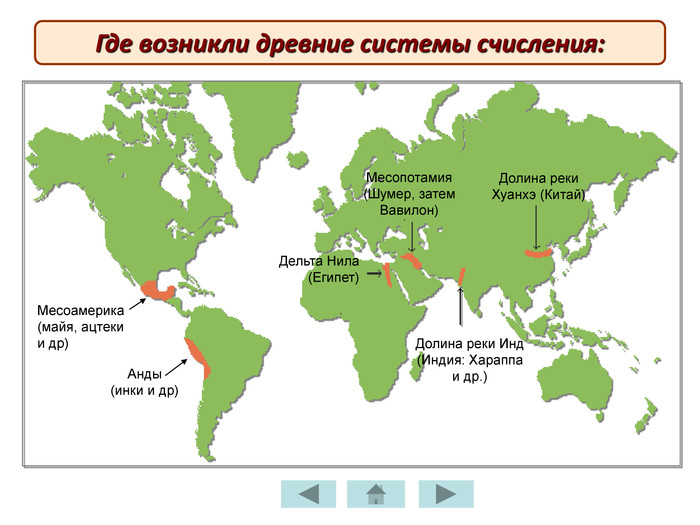
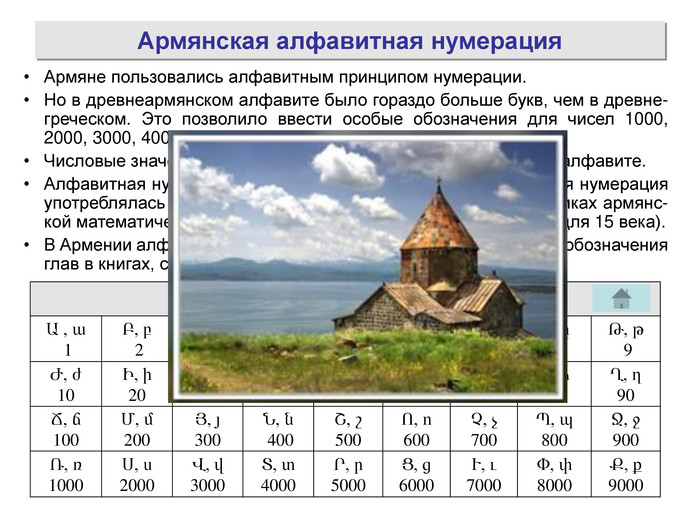
Презентація «История нумерации»
Про матеріал
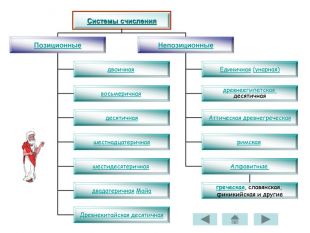
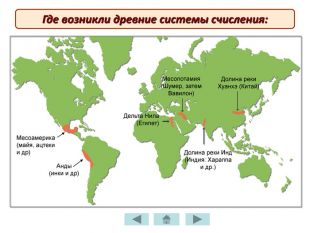
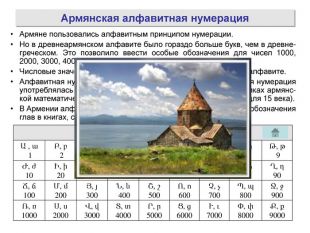
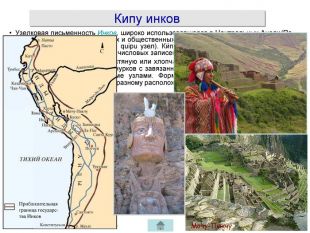
Жук Олена Борисівна пропонує вашій увазі мультимедійну презентацію «История нумерации» (російською мовою) з теми «Кодування». Перегляд презентації здійснюється у режимі «Тільки читання» після скачування архіву та його розархівування. Зміст архіву
Перегляд файлу
Перегляд файлу
Перегляд файлу тимчасово недоступний.
Перегляд файлу
Перегляд файлу тимчасово недоступний.
Перегляд файлу
Перегляд файлу
Зміст слайдів
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку