Презентація" Коло описане навколо трикутника. Взаємне розміщення кіл на площині"
Про матеріал
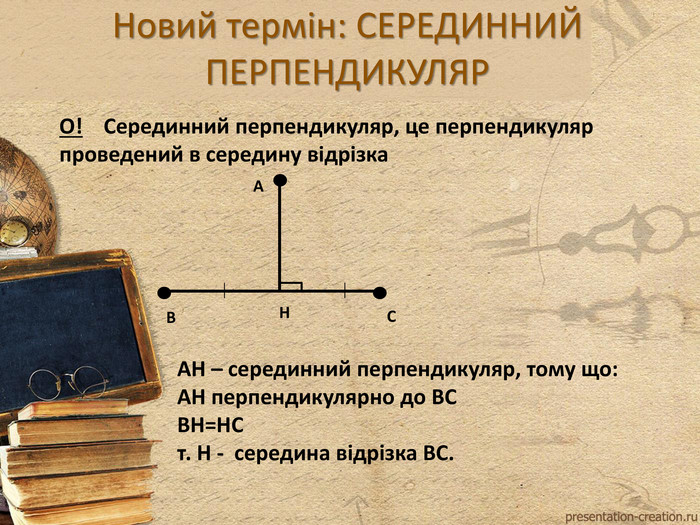
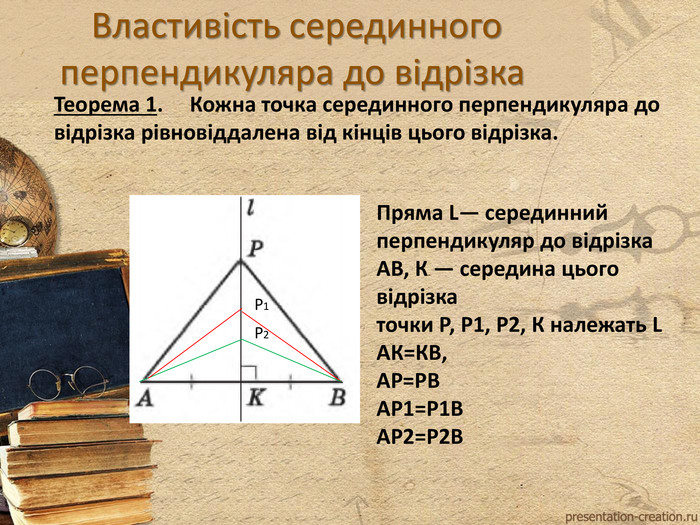
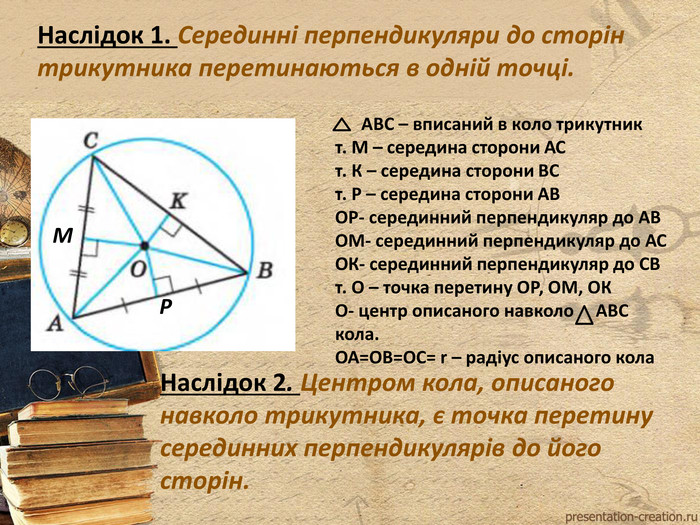
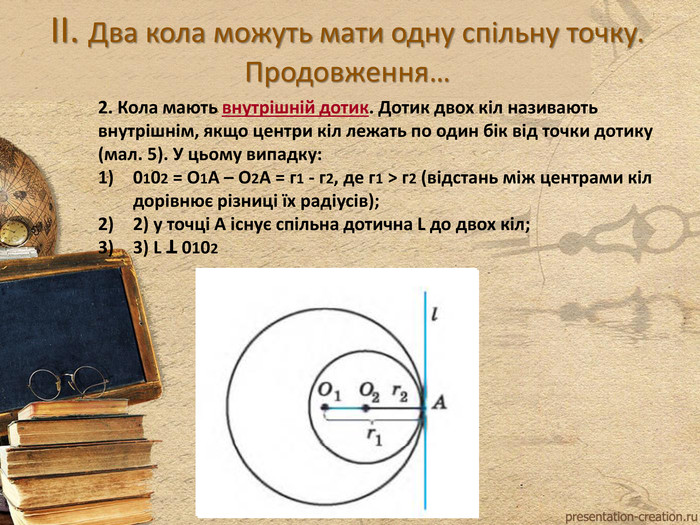
Вводить поняття описаного навколо трикутника кола, Серединного перпендикуляра. Розглядаються варіанти взаємного розміщення кіл на площині. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






























-

Данилець Вікторія
10.04.2025 в 15:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ізотова Олена
03.04.2025 в 09:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
30.04.2023 в 17:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самікова Ірина Олександрівна
19.04.2023 в 13:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
16.02.2023 в 13:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука