Нестандартний урок-ролева гра: «Судове засідання»

Урок по темі  «Розв’язування задач. Кути між прямими, що перетинаються»

Методичний коментар

Урок-ролеву гру «Судове засідання» доцільно проводити при повторенні та  закріпленні вивченого матеріалу по окремо взятій темі. Найоптимальніше можливості даної ролевої гри використовуються при вивченні геометрії, оскільки розв’язування геометричних задач вимагає чіткого обґрунтування кожного кроку  розв’язання.

Даний тип уроку дає можливість отримати уявлення про спрощену процедуру прийняття судового рішення та провести рольову гру – судовий процес за участю 4-х сторін: судді, адвоката, прокурора і свідків (можлива участь позивача, відповідача, секретаря тощо).

Роль судді може виконувати як учитель, так і учень. Це головна роль, яка вимагає швидкої реакції на всі ситуації, що виникають на уроці.

Адвокат намагається захистити, допомогти під час розгляду справи (тобто, при розв’язуванні задач). Він же готує свідчення для  захисту справи (задачі).

Прокурор знайомить усіх присутніх зі справою, що розглядається у ході засідання, і вимагає її вирішення.

Свідком може бути будь-який учень класу, якщо його виступ пов'язаний із визначенням понять, означень, доведенням теорем. Окрім того, свідки можуть бути заздалегідь підготовлені – це учні, які наводять історичні довідки, доведені цікаві факти відповідно до теми судового засідання.

Ця форма уроку приваблива тим, що в ній стикаються протилежні погляди на суть окремих питань.

Тема уроку. Розв’язування задач. Кути між прямими, що перетинаються.

Клас: 7 клас.

Тип уроку: урок закріплення знань, умінь і навичок.

Форма проведення: рольова гра «Судове засідання».

Використані технології навчання: особистісно-орієнтована, технології групової навчальної діяльності і формування творчої особистості,   ігрова технологія.

Мета уроку: узагальнити і систематизувати знання та вміння учнів з теми, формувати уміння застосовувати здобуті знання на практиці; розвивати логічне мислення учнів, навики культури оформлення геометричних задач, вміння робити висновки, висловлювати та відстоювати свою думку; розвивати інтерес до математики в цілому та до геометрії зокрема.

Дійові особи:  суддя, прокурор, адвокат, свідки захисту та звинувачення.

Обладнання: комп’ютер, мультимедійний проектор, таблички  «Суддя»,  «Прокурор», «Адвокат», підручники, бланки завдань.

Структура уроку

Хід уроку

І. Організаційний момент.

II. Повідомлення теми і мети уроку.

Вступне слово вчителя. «Геометрія – це широкий розкішний краєвид, відкритий всім тим, кому мислення доставляє справжню радість» – сказав у свій час відомий британський полярний дослідник 20 століття сер Вівіан Ернест  Фукс. І хоча вивчення геометрії ми розпочали зовсім недавно, проте ви вже мали можливість пересвідчитися, що уміння розв’язувати геометричні задачі –  таке ж практичне мистецтво, як уміння плавати або бігати на лижах, а    навчитися йому можна тільки шляхом наслідування та виконання вправ.

У різноманітності геометричних фігур, зокрема кутів, суміжні та вертикальні кути посідають чільне місце, а вміння розв’язувати задачі із використанням їх властивостей є надзвичайно важливим вмінням при вивченні планіметрії. Тож тема  нашого уроку «Розв’язування задач. Кути між прямими, що перетинаються» є настільки важливою, що розібратися з нею нам допоможе тільки судове засідання. Не будемо гаяти часу і розпочнемо наш процес.

III. Судове засідання

Секретар. Встати! Суд  іде!

(Суддя, прокурор та адвокат займають свої місця)

Суддя. Прошу сідати! Шановні пані та панове, засідання суду оголошую відкритим. Слухається справа кутів між прямими, що перетинаються. Засідання веде суддя – _________________ при секретарі _______________. Звинувачення підтримує прокурор ____________, захист здійснює адвокат ______________.

Для оголошення обвинувачення слово надається прокурору.

Прокурор. Ваша честь, поважана публіка! До суду надійшла колективна заява групи учнів 7 класу, в якій вони звинувачують суміжні і вертикальні кути у тому, що останні засмічують своїми означеннями та властивостями світлий учнівський розум, сіють хаос в їх знаннях і плутають їх в знаходженні шляхів розв’язання геометричних задач, особливо тих, в яких мова іде про кути між прямими, що перетинаються, і взагалі, учні переконані, що дану тему  потрібно прибрати зі шкільного курсу математики.

Адвокат. Заперечую, ваша честь. Тема «Суміжні і вертикальні кути» є і має залишатися невід’ємною складовою шкільного курсу математики. Адже перші відомості про суміжні кути зароджувались під час проектування доріг чи каналів, які перетинаються, при будівництві внутрішніх стін будинків. Вертикальні кути розглядав у своєму підручнику ще давньогрецький філософ,  математик і астроном Фалес Мілетський.  Нині на території індіанської резервації племені Навахо, є унікальний пам'ятник чотирьох кутів, на місці якого перетинаються відразу чотири штати Сполучених Штатів Америки: Арізона, Колорадо, Нью-Мексико і Юта. Вам нічого не нагадує цей пам’ятник, пане прокуроре?

       Прокурор. Ваша честь, поглянувши на зображення пам’ятника, люб’язно надане паном адвокатом, ми, власне, бачимо дві прямі, що перетинаються. В результаті чого утворилося чотири прямі кути. Звідси, наскільки я розумію, і назва пам’ятника. Але яке відношення це має до нашої справи?

Адвокат. Ваша честь, при перетині двох прямих утворюється не просто чотири кути, які помітив пан прокурор, серед них можна виділити дві пари вертикальних та чотири пари суміжних кутів.  Оскільки суміжні кути – це два кути, у яких одна сторона спільна, а дві інші є доповняльними променями, то на даному зображенні можна виділити чотири пари суміжних кутів: Юта-Колорадо, Колорадо-Нью-Мексико, Нью-Мексико-Арізона та Арізона-Юта (адвокат показує суміжні кути на слайді). Штати Юта-Нью-Мексико та Арізона-Колорадо утворюють вертикальні кути, бо два кути називаються вертикальними, якщо сторони одного є доповняльними променями до сторін другого (демонструє).

Суддя. Пане адвокате, виходить, що суміжні і вертикальні кути – це парні кути.  (мрійливо) Дійсно, геометрія є наймогутнішим засобом для розвитку наших розумових здібностей і дає нам можливість правильно мислити і міркувати.

Прокурор. Ваша честь, але, якщо на одному рисунку буде така кількість кутів, то як розв’язувати задачі? Саме складність таких задач і є предметом нашого судового засідання.

Адвокат. Своєрідність геометрії, що виділяє її серед інших розділів математики, та й усіх наук взагалі, полягає в нерозривному органічному поєднанні живої уяви з суворою логікою. Тож для розв’язування задач, достатньо вирізняти  суміжні і вертикальні кути на рисунку та пам’ятати їх властивості, які є доволі простими і для запам’ятовування, і для використання. Судіть самі: по-перше, сума суміжних кутів 180⁰, по-друге, вертикальні кути рівні.

Прокурор. Зачекайте, пане адвокате. Настільки серйозне твердження вимагає обґрунтування.

Суддя. Для  обґрунтування властивостей суміжних та вертикальних кутів до зали суду запрошуємо свідків … та ….

 Свідок 1. (за готовим рисунком усно доводить властивість суміжних кутів).

Суддя. Зачекайте, пане свідок. Мені б хотілося пересвідчитися, що слухачі справи засвоїли викладене вами твердження. Прошу вас (звертається до класу) дати відповіді на запитання:  чи можуть суміжні кути дорівнювати 75⁰ і 80⁰; 94⁰ і 96⁰;  83⁰ і 97⁰? Чому? (учні відповідають на запитання) Молодці. Що ж, продовжимо слухання справи і вислухаємо докази свідка …

Свідок 2. (записує доведення властивості вертикальних кутів на дошці, а після виступу Свідка 2 коментує доведення)

Адвокат. Як бачите, ваша честь, доведення властивостей доволі просте і зрозуміле пересічному школяреві.

Прокурор. Ваша честь, якщо все настільки просто, то можливо учні зможуть без особливих зусиль виконати підготовлені мною вправи?

Суддя.  Не заперечую. Запрошуємо до зали суду для розв’язання усних вправ свідка …

Прокурор. Шановний свідок, прошу вас розв’язати наступні завдання.

1.               Що можна сказати про кожний з вертикальних кутів, якщо: їх сума більша за 180⁰; їх сума дорівнює 180⁰; їх сума менша за 180⁰?
2.               Чи можуть суміжні кути бути обидва:  гострими; тупими;  прямими?
3.               Один із чотирьох кутів, що утворилися при перетині двох прямих, дорівнює 120°.  Яку градусну міру має кожен з решти кутів?

(свідок 3, обґрунтовуючи кожне своє твердження, виконує завдання, що демонструються на слайді)

Суддя. Свідок … яскраво довів, що із завданнями даного типу справиться навіть п’ятикласник. То де ж усі ті складнощі, які  сіють хаос в світлих головах наших учнів?

Адвокат. Ваша честь, геометрія сповнена пригод, тому що за кожним завданням ховається пригода думки. Розв’язати задачу – це значить пережити пригоду. Тож прошу вашого дозволу на наступну пригоду:  знайти всі кути, які утворилися при перетині двох прямих, якщо сума трьох з них дорівнює  250⁰.

Суддя. Не заперечую. Для розв’язання задачі до зали суду запрошуємо свідка … (переглядаючи скорочений запис умови) Пане адвокате, що це за дивний знак в умові задачі? Що він означає?

(свідок 4 пояснює призначення знаку перетину і, обґрунтовуючи кожне своє твердження, розв’язує задачу усно. Секретар суду виводить розв’язання на екран)

Суддя. Мушу погодитися, все достатньо просто і зрозуміло. Пане прокурор, а ви маєте завдання для учнів?

Прокурор. Так, ваша честь, дозвольте запропонувати учням наступну задачу: знайти всі кути, які утворилися при перетині двох прямих, якщо один з них на 42⁰ більший від другого.

Суддя. Не заперечую.  Прошу дану задачу розв’язати свідка…

(свідок 5  пояснює про які кути іде мова. Секретар скорочений запис умови задачі виводить на екран, а свідок на дошці розв’язує задачу)

Адвокат.  Пане прокуроре, щойно ви отримали черговий доказ того, що ніяких складнощів при розв’язуванні задач не виникає. І щоб переконати вас остаточно, пропоную розв’язати ще одну задачу: знайти всі кути, які утворилися при перетині двох прямих, якщо сума двох з них дорівнює  246⁰ .

Суддя. Проте, пане адвокате, поки свідок … розв’язуватиме запропоновану вами задачу, прошу вас розв’язати задачу від судді, потім прокоментувати нам хід її розв’язання.

Задача від судді. Знайти всі кути, які утворилися при перетині двох прямих, якщо градусні міри двох з них відносяться як 7:11.

Секретар. Запрошую до зали суду для розв’язання задачі від адвоката свідка …

(свідок 6 пояснює про які кути іде мова і, коментуючи, розв’язує задачу на дошці, адвокат виконує завдання судді самостійно, а по завершенню виступу свідка, пояснює хід її розв’язання)

Адвокат. Ваша честь, підсумовуючи все викладене в ході  нашого судового засідання,  дозвольте сформулювати алгоритм розв’язування задач на кути, утворені при перетині двох прямих.

Суддя. Прошу.

Адвокат. По-перше, якщо мова йде про суму двох кутів, то це вертикальні кути, бо сума суміжних 180⁰. Врахувавши, що вертикальні кути рівні, вказану суму ділимо на 2, а далі знаходимо кути, суміжні до даних.

По-друге, якщо за умовою задачі відомо відношення кутів, їх різниця, чи вказано, що один з кутів у декілька разів більший (менший) за другий, то в цьому випадку ми маємо розглядати спочатку суміжні кути, а потім вертикальні до них.

Тож, шановний суд! Перш ніж засудити чи виправдати суміжні та вертикальні кути прошу врахувати доступність і зручність використання властивостей даних кутів до розв’язування задач.

Прокурор. Ознайомившись з матеріалами нашої справи, я переконався в тому, що математику не можна вивчати, спостерігаючи, як це робить сусід!  Щоб навчитися мистецтву розв’язування геометричних задач загалом, і задач на знаходження кутів між прямими, що перетинаються, зокрема, потрібно, ґрунтовно вивчивши теорію, сідати і наполегливо працювати, відчеканюючи свої уміння з кожною наступною задачею.

Секретар. Прошу всіх встати для оголошення вироку!

Суддя. На підставі Закону України «Про освіту», державних стандартів освіти, розділів програми з математики для 7 класу, вислухавши обидві сторони, розглянувши всі представлені матеріали по справі, суд вирішив:

1. Підсудних виправдати.

2. Тему «Суміжні і вертикальні кути. Кути між прямими, що перетинаються» ні в якому разі зі шкільної програми не виключати.

3. Сформульований адвокатом алгоритм розв’язування задач на кути між прямими, що перетинаються, вивчити всім учасникам процесу напам’ять.

4. Виступи  учасників процесу оцінити наступним чином: _____________

____________________________________________________________________

5. Всім повторити параграфи  5-6 і виконати вправи № 120, ст. 32, №8,  ст. 35.

Вирок остаточний і оскарженню не підлягає! Судове засідання оголошується закритим!

Секретар. Встати! Суд йде!

ІV. Підсумки уроку. Сподіваюся, що наше судове засідання все ж переконало вас у тому, що тема «Суміжні і вертикальні кути. Кути між прямими, що перетинаються» є доступною та зрозумілою, а для того, щоб вона розкрила вам свої таємниці, потрібно наполегливо та натхненно працювати. На завершення нашого уроку пропоную вам невеличкий математичний диктант.

Математичний  диктант

1. Назвіть суміжні і вертикальні кути на рисунку.

Суміжні _______________________________________________________.

Вертикальні ____________________________________________________.

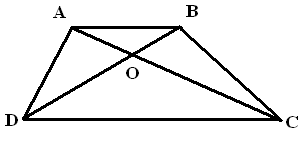
2. Скільки пар вертикальних кутів утвориться при перетині двох прямих? _________.
3. Скільки пар суміжних кутів утвориться при перетині двох прямих? __________.
4. Якщо один із суміжних кутів тупий, то другий _________________.
5. Сума суміжних кутів ______________.
6. Вертикальні кути _________________ .
7. Якщо сума двох кутів, що утворилися при перетині двох прямих 200⁰, то це ________________________ кути, градусні міри яких дорівнюють _______________________.
8. Якщо один із суміжних кутів 90⁰, то другий ___________.
9. Якщо один із кутів, що утворилися при перетині двох прямих 45⁰, то градусні міри трьох інших кутів ________________________________.
10. Сума кутів між прямими, що перетинаються дорівнює __________.

(питання математичного диктанту демонструються на слайді, учні самостійно виконують завдання на тест-аркушах, які здають вчителю)

 Заключне слово вчителя. Пам’ятайте, хто з дитячих років займається математикою, той розвиває увагу, тренує свій мозок, свою волю, виховує наполегливість і завзятість у досягненні мети.

Дякую за увагу!

Список використаних джерел

1. Істер О.С. «Геометрія», підручник для 7 класу загальноосвітніх навчальних закладів, Київ, «Ґенеза», 2015. – 184 с.
2. Істер О.С. «Геометрія. 7 клас: Вправи. Самостійні роботи. Тематичні контрольні роботи. Завдання для експрес-контролю», вид. 2-е, переробл. і доповн., Тернопіль: Навчальна книга – Богдан, 2016. – 136 с.
3. Карпінська І.Й. Нестандартні уроки з математики. - Тернопіль: Підручники і посібники, 2001.  –  с . 9-10