Презентація "Квадратне рівняння як модель текстової задачі 3"
Про матеріал
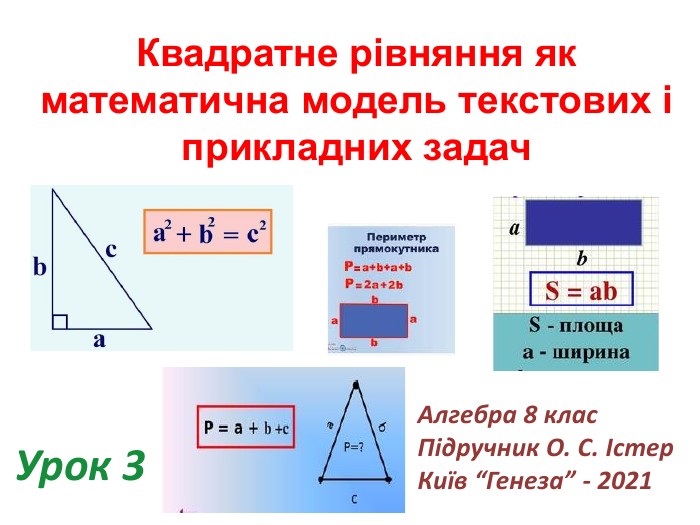
Презентація до теми "Квадратне рівняння як математична модель текстових і прикладних задач" рекомендована для проведення уроків алгебри у 8 класі в дистанційному форматі. Пристосована до підручника "Алгебра 8" О. С. Істер 2021. Має Алгоритм розв'язування задач, перевірку домашньої роботи і класну роботу. Вчитель, користуючись цим матеріалом, може пристосувати його до своїх потреб, змінивши зміст. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 8 клас (Істер О. С.)
До уроку
Розділ 3. Квадратні рівняння Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку