Презентація "Квадратні нерівності"
Про матеріал
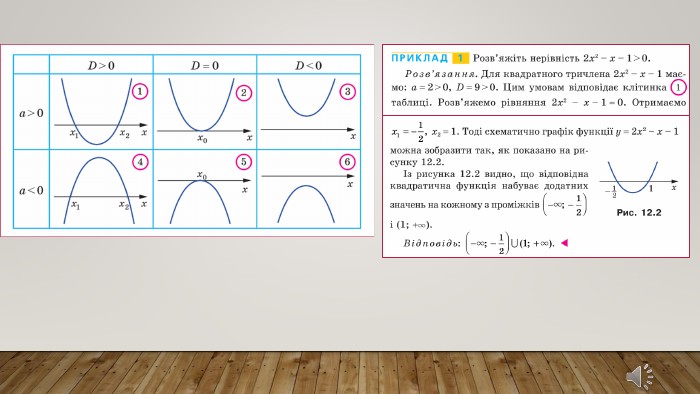
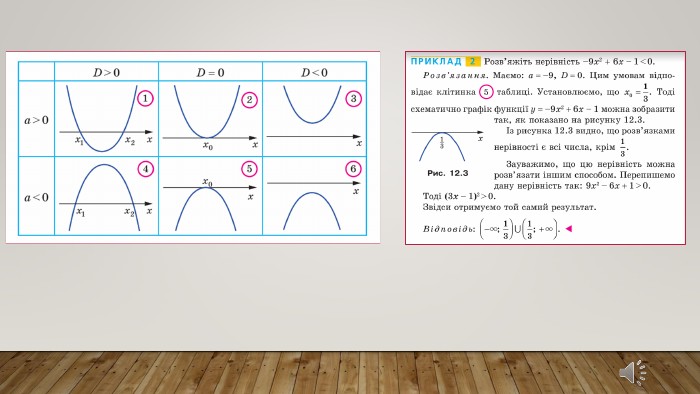
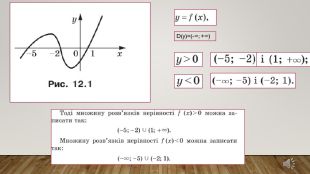
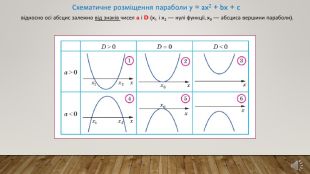
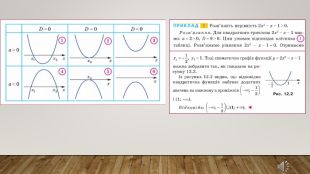
Подання нового матеріалу: введення поняття квадратної нерівності, розгляд випадків розміщення параболи відносно осі абсцис залежно від знаків чисел а і D, наведення прикладів розв'язання квадратних нерівностей. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
12. Розв’язування квадратних нерівностей Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку