Презентація "Метричні співвідношення в прямокутному трикутнику"

Про матеріал

Ця презентація була створена мною для учнів, які перебувають у 8 класі та вивчають математику на поглибленому рівні, і вчителів, які, власне, викладають геометрію учням 8 класу. Матеріал, що є основою цієї презентації, взятий з підручника Мерзляка(більш детально на титульному слайді), достатньо структурований: є зміст, цілі, повторення минулих тем(базові поняття: перпендикуляр, похила, проекція похилої на пряму; теорема Піфагора), коротоенька теорія по темі заняття, приклади розв'язування деяких задач, купа практичних завдань(практикум на 5 завдань), тестування, ДЗ.

Перегляд файлу

ДАЙТЕ ВІДПОВІДІ НА ЗАПИТАННЯ

Який трикутник називають прямокутним?

Як називаються сторони прямокутного трикутника та як вони розм щен ?

Що таке похила та її проекц я на пряму?

Що називається висотою трикутника?

ПРАВИЛЬНІ ВІДПОВІДІ НА ЗАПИТАННЯ

0 Який трикутник називають прямокутним?

1 Як називаються сторони прямокутного трикутника та як вони розмщен ?

Прямокутнийтрикутник — трикутник, один з кут в якого прямий.

Сторони прямокутного трикутника мають власн назви. Дв сторони, що утворюють прямий кут називаються катетами(a,b), а третя сторона — г потенузою(c).

За теоремою Пфагора можна знайти будь-яку сторону прямокутного трикутника, якщо в дом дв нш сторони. За теоремою П фагора квадрат г потенузи дор внює сум квадрат в катет в.

Прямокутний трикутник(∠ACB = 90°)

Зв дси можна знайти нш сторони прямокутного трикутника.

ПРАВИЛЬНІ ВІДПОВІДІ НА ЗАПИТАННЯ

3 Що називається висотою трикутника?

2 Що таке похила та її проекц я на пряму?

Висота трикутника — в др зок, проведений з вершини трикутника до прямої, яка м стить сторону протилежну вершин , та перпендикулярний до неї. Висотою також називають довжину висоти трикутника, тобто в дстань в д вершини до протилежної сторони. Основою висоти називається точка перетину висоти та прямої, яка м стить протилежну сторону.

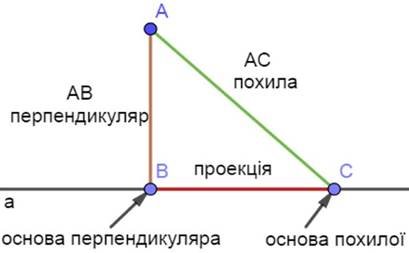Перпендикуляром, проведеним з деякої точки до заданої прямої, називається в др зок, що лежить на прям й, перпендикулярн й до заданої прямої з к нцями в задан й точц , точки, що лежить на задан й прям й. К нець перпендикуляра, що лежить на прям й, до якої в н проведений, називається основою перпендикуляра.

Похила — будь-який в др зок, проведений з точки на пряму, в дм нний в д перпендикуляра. К нець похилої, що лежить на прям й, до якої вона проведена, називається основою похилої.

В др зок, що сполучає к нець перпендикуляра похилої до прямої, проведених з одн єї точки, називається проекц єю похилої на пряму.

КОРОТЕНЬКА ТЕОРІЯ ПО ТЕМІ ЗАНЯТТЯ

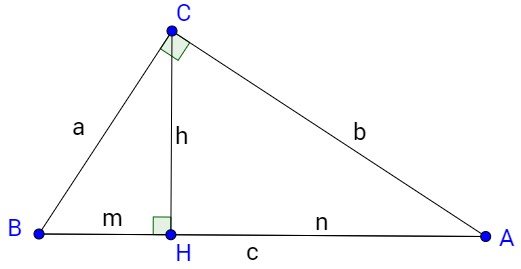На рисунку в др зок CH — висота прямокутного трикутника ABC (∠ACB=90°).

В др зки AH HB називають проєкц ями катет в AC CB в дпов дно на г потенузу.

Лема. Висота прямокутного трикутника, проведена до г потенузи, д лить трикутник на два под бних прямокутних трикутники, кожен з яких под бний даному трикутнику.

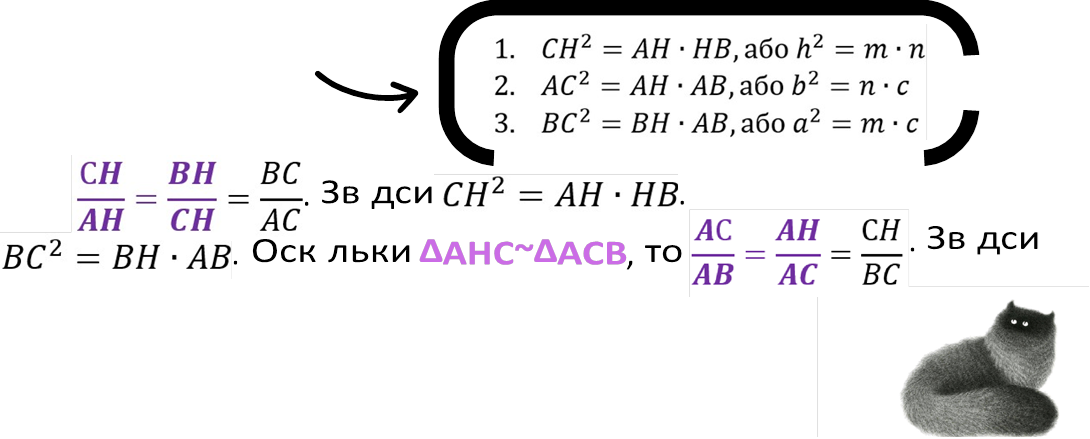Доведення леми*. У ΔABC CН — висота, ∠B=90°-∠A. У ΔВНС ΔСНА ∠BHC=∠CHA=90°, ∠ACH=90°— ∠A=∠B, тобто ∠CBH=∠ACH. Тод за І ознакою под бност ΔBHC~ΔCHA. У ΔBHС ΔВСА

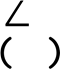∠BHC=∠BCA=90°, ∠B — сп льний, тод за І ознакою под бност ΔBHC~ΔBCA. У ΔАНС ΔАСВ AHC=∠ACB=90°, ∠A — сп льний, тод за Іознакою под бност ΔAHC~ΔACB. Що й треба було довести. Теорема^▲ . Квадрат висоти прямокутного трикутника, проведеної до г потенузи, дор внює добутку проєкц й катет в на г потенузу. Квадрат катета дор внює добутку г потенузи та проєкц ї цього катета на г потенузу.

Доведення теореми*. Оск льки ΔBHC~ΔCHA, то

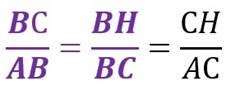Оск льки ΔBHC~ΔBCA, то . Зв дси

. Що й треба було довести.(_▲)

ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ДЕЯКИХ ЗАДАЧ

Задача 0. Дано два в др зки, довжини яких дор внюють a b. Побудуйте трет й в др зок, довжина якого дор внює √ab.

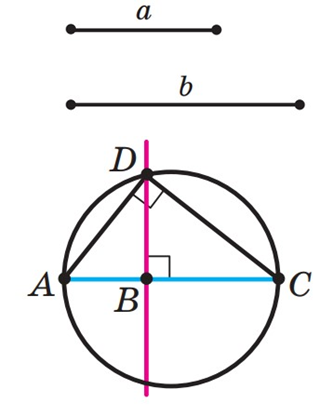Розв’язання. Розглянемо трикутник ADC(∠ADC=90°), у якому в др зок DB є висотою. Маємо: DB=√AB⋅BC. Якщо позначити AB=a, BC=b, то DB=√ab.

Проведений анал з показує, як провести побудову.

На дов льн й прям й позначимо точку A та в дкладемо посл довно в др зки AB BC так, щоб AB=a, BC=b. Побудуємо коло з д аметром AC. Через точку B проведемо пряму, перпендикулярну до прямої AC. Нехай D — одна з точок перетину прямої та кола.

Доведемо, що в др зок DB — шуканий. Справд , ∠ADC=90° як вписаний кут, що спирається на д аметр AC. Тод за теоремою 1 DB=√AB⋅BC, тобто DB=√ab._▲

--------------------------------------------------------------------------------------------------------------------------------------

Задача 1. На катет AC прямокутного трикутника ABC як на д аметр побудовано п вколо, яке перетинає г потенузу AB у точц M так, що AM:MB=1:3. Знайд ть кути трикутника ABC.

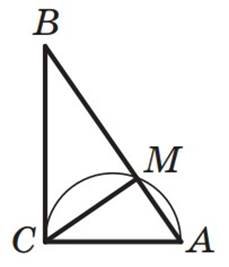Розв’язання. Оск льки кут CMA вписаний, що спирається на д аметр, то CM⊥MA.

Нехай AM=x, тод MB=3x. За теоремою 1 AC²=AM⋅AB, тобто AC²=x⋅4x. Зв дси AC=2x.

Отримали, що в прямокутному трикутнику ABC катет AC удв ч менший в д г потенузи. Зв дси ABC=30°, BAC=60°.

Задача 2. Знайд ть катети прямокутного трикутника, висота якого д лить г потенузу на в др зки, один з яких на 3 см менший в д ц єї висоти, а другий — на 4 см б льший за висоту. Розв’язання.

Задача 3. Перпендикуляр, опущений з точки перетину д агоналей ромба на його сторону, дор внює 2 см д лить цю сторону на в др зки, як в дносяться як 1:4. Знайд ть д агонал ромба. Розв’язання.

Задача 4. Знайд ть периметр р вноб чної трапец ї з основами 7 см 25 см, д агонал якої перпендикулярн до б чних стор н.

Задача 5. Д агональ р вноб чної трапец ї перпендикулярна до б чної сторони, яка дор внює 12 см. Знайд ть середню л н ю трапец ї, якщо рад ус кола, описаного навколо трапец ї, дор внює 10 см. Розв’язання.

Задача 6. У прямокутну трапец ю вписано коло. Точка дотику д лить б льшу б чну сторону на в др зки завдовжки 8 см 50 см. Знайд ть периметр трапец ї.

Розв’язання.