Урок з геометрії для учнів 8 класу з теми: " Розв'язання прямокутних трикутників"
Розв’язання прямокутних трикутників
(урок з геометрії в 8 класі)
Мета: формувати вміння та навчати учнів розв’язати задачі на застосування теореми Піфагора та її наслідків, властивостей прямокутного трикутника, співвідношення між сторонами і кутами прямокутного трикутника, удосконалювати навички виконання тестових завдань, розвивати математичну мову, логічне мислення, обчислювальні навички, предметну компетентність, виховувати увагу, самостійність, пізнавальну активність, наполегливість, інтерес до геометрії, почуття патріотизму, розширити знання учнів про Купʼянщину.
Обладнання: зошит, ручка, указка, ноутбук, мультимедійний проектор, екран, презентація до уроку, роздатковий матеріал, мобільний телефон, використовується підручник з геометрії для 8 класу (автор А.Мерзляк).
Тип уроку: урок формування вмінь та навичок.
Форма уроку: геометрично-краєзнавчий серіал "Куп’янщина – моя Батьківщина".
Хід уроку
І. Організаційний момент.
Учитель.
Колиска мого дитинства –
Усмішка весни.
П’ють тут усі джмелі
Ягідний сік полуниць.
На берегах Оскола
Сяють церков куполи.
Ь
Колиска твого дитинства ...
Де її знайти ?
(У Куп’янську)
Учитель. У житті людини завжди були важливими родичі, кохані, друзі. А ще – рідна Батьківщина, де вона народилася, де її належить жити, у чию долю та розвиток, робити свій внесок. Це наш Куп’янськ. Сьогодні у нас незвичайний урок, геометрично-краєзнавчий серіал "Куп’янщина – моя Батьківщина". Ви будете активними учасниками цього серіалу, бо будете дізнаватися багато цікавого про Куп'янщину, і в цьому нам допоможе геометрія.
Тема нашого уроку "Розв’язання прямокутних трикутників". На уроці ми будемо вчитися розв’язувати задачі на застосування теореми Піфагора та її наслідків, властивостей прямокутного трикутника, співвідношення між сторонами і кутами прямокутного трикутника.
ІІ. Актуалізація опорних знань учнів.
1.Учитель. Щоб переглянути серію № 1, потрібно виконати геометричне завдання. Діти! Ви знаєте, що у здоровому тілі – здоровий рух. А щоб бути здоровими, потрібно кожного ранку робити: "Що?". Діти відповідають: "Зарядку". Щоб добре попрацювати на уроці, потрібно також зробити геометричну зарядку. Зараз ми з вами виконаємо геометричну зарядку під гаслом "Геометрія – гімнастика розуму".
Гра "Усна геометрична розминка".
Завдання. Вписати числа в геометричні фігури, застосовуючи значення тригонометричних функцій для кутів 30°- 60° і математичні дії, назвати прізвище куп’янчанина, майстра спорту з легкої атлетики, олімпійського факелоносця, який ніс олімпійський вогонь під час Олімпіади - 80.
1) 1980 • tg 45° =
2) 77 + 4 • (cos 30° • sin 60°) =
3) ctg 45° • 1974 =
4) 14 + (2 • sin 30°) =
5) 78000 • (tg 30° • tg 60°) • (ctg 30° • ctg 60°) =
6) 
7) 240 • cos 60° • 2sin 30° =
Таблиця відповідей
|
Номер приклада |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Відповідь |
1980 |
80 |
1974 |
15 |
78000 |
32 |
120 |
|
Буква |
Є |
Л |
М |
О |
В |
Ф |
І |
|
Прізвище |
Є |
Л |
Ф |
І |
М |
О |
В |
Серія 1 "Гордість Куп’янщини"
Єлфімов Олександр Миколайович
Олімпійський факелоносець, майстер спорту з легкої атлетики, вчитель фізичної культури Смородьківської загальноосвітньої школи І-ІІ ступенів.
- 1980 році ніс олімпійський вогонь під час Олімпіади-80
- 1974 рік найсильніший стайєр у Радянському Союзі
- 15 років був у складі збірної команди Української республіки з легкої атлетики.
- 78 000 км його загальний пробіг у 32 країнах світу
- 120 км пробігав за день під час тренувань.
2. Учитель.
2.1. Для розв’язування задач нам з вами треба повторити теорему Піфагора, означення синуса, косинуса, тангенса, котангенса гострого кута прямокутного трикутника. І це ми зробимо за допомогою кросворда.
2.2. А також, для розв’язку задач будуть потрібні властивості деяких фігур із усної геометричної розминки.
Індивідуальна робота у дошки.
"Інтерактивна вправа. Дописати пропущену властивість"
1. Прямокутник.
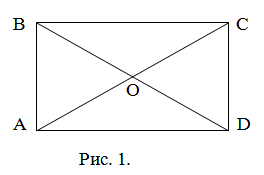ABCD – прямокутник
∠А + ∠В = ...
АВ = ...
ВС = ...
∠А = ∠...
АС = ...
АО = ...
2. Ромб.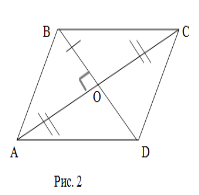 
ABCD – ромб
АВ = ....
АО = ...
ВО = ...
АС 
...
∠ВАО = ∠ ...
∠А+ ∠В = ...
∠А= ...
∠В = ...
△АВО –
3. Рівнобічна трапеція.
ABCD – рівнобічна трапеція
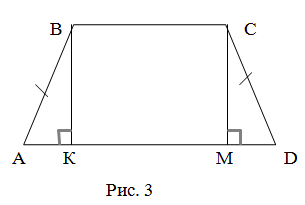АВ = ...
АК = ...
ВС = ...
∠А + ∠В = ...
∠А =∠ ...
Завдання. Розгадуючи кросворд, назвати назву улюбленого шкільного предмета вченого математика України, автора завдань ЗНО з математики, випускника Куп’янської загальноосвітньої школи № 6.
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
Запитання до кросворду.
- Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині ... (гіпотенуза)
- Синусом гострого кута прямокутного трикутника називається відношення... (протилежного) катета до гіпотенузи
- Косинусом гострого кута прямокутного трикутника називається відношення... (прилеглого) катета до гіпотенузи
- У прямокутному трикутнику будь-який катет ... (менший) гіпотенузи
- Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до ... (прилеглого)
- У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів ... (катетів)
- Квадрат будь-якого катета прямокутного трикутника дорівнює ... (різниці) квадрата гіпотенузи і квадрата іншого катета
- Два кути прямокутного трикутника, що в сумі становлять 90°, є ... (гострі)
- Якщо катети прямокутного трикутника 3 і 4, а гіпотенуза ... (п’ять), то це єгипетський трикутник.
|
|
|
|
|
|
|
|
1 |
г |
і |
п |
о |
т |
е |
н |
у |
з |
и |
|
|
2 |
п |
р |
о |
т |
и |
л |
е |
ж |
н |
о |
г |
о |
|
|
|
|
|
3 |
п |
р |
и |
л |
е |
г |
л |
о |
г |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
м |
е |
н |
ш |
и |
й |
|
|
|
|
|
|
|
|
5 |
п |
р |
и |
л |
е |
г |
л |
о |
г |
о |
|
|
|
|
|
|
|
|
|
|
6 |
к |
а |
т |
е |
т |
і |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
р |
і |
з |
н |
и |
ц |
і |
|
|
|
|
|
|
8 |
г |
о |
с |
т |
р |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
п |
ʼ |
я |
т |
ь |
|
|
|
|
|
|
|
Серія 2. Провідний математик України в галузі геометрії.
Лисиця Віктор Тимофійович
Кандидат фізико-математичних наук, доцент факультету математики і інформатики, завідувач кафедри вищої математики і інформатики Харківського Національного Університету ім. В.Н. Каразіна.
Автор завдань ЗНО з математики.
13 – науково-методичних робіт.
14 науково-методичних робіт з геометрії.
22 виступи на конференціях.
3. Учитель. Зараз перевіримо ваші вміння застосовувати правила до розв’язку задач.
Геометричне завдання "Пропущений розв’язок"
Завдання. За даними на рисунку знайти невідомі елементи у прямокутному трикутнику. Знайти суму всіх натуральних чисел, отриманих у розв’язку задач. Дізнаємося, як це число пов’язане з випускником Куп’янського НВК №2.
Задачі І варіант.
1) А Дано: △АВС, ∠С=90°, ВС=2 см, ∠А=30°
30° Знайти: АВ, АС, ∠В
Розв’язання
1) ∠В = 90° - ...
С 2 В 2) АВ = ... • СВ =
Рис. 4 3) АС = 
2) А Дано: △АВС, ∠С=90°, АС=СВ, АВ =
см
Знайти: АС, ВС, ∠А, ∠В
Розв’язання
С В 1) ∠А = ∠ ...
Рис. 5 2) Нехай АС=х(см), х2+х2 =()2 2х2 =... х=...
3) АС = ...
Задачі ІІ варіант.
1) А Дано: △АВС, ∠С=90°, ВС=3см, ∠В=60°
Знайти: АВ, АС, ∠А
Розв’язання
60° 1) ∠А = 90° - ...
С 3 В 2) АВ = 2 • ...
Рис. 6 3) АС = 
2) А Дано: △АВС, ∠С=90°, ∠А=30°, АС=6см,
30° Знайти: АВ, ВС, ∠В
6 Розв’язання
1) ∠В = 90° - ...
С В 2) tg 30° = 
ВС = ...
Рис. 7 3) АВ = 2 • ...
Учитель. В сумі вийшло число 12. Як же це число пов’язане з випускником Куп’янського НВК №2
Серія 3. Майбутня авіаційна еліта України.
Хілєс – Гунченко Віталій
Випускник Куп’янського НВК №2
Навчався у Харківському Національному Аерокосмічному Університеті ім. М.Є.Жуковського
І місце у конкурсі "Авіатор - 2017".
І місце у ІІ турі Всеукраїнської студентської олімпіади з нарисної геометрії та геометричного моделювання на ПЕОМ.
Відвідав на цей час 12 країн світу.
ІІІ. Формування вмінь і навичок учнів.
Учитель. Все необхідне повторили, переходимо до розв’язання задач.
3.1. Учитель. Математика у майбутньому.
Практична задача. Числові дані задачі № 623 допоможуть назвати прізвище найвідомішого українського гросмейстера, портрет якого розміщено в музеї інтелектуальних видів спорту в Шанхаї, випускника Куп’янської гімназії № 2.
Серія 4. Інтелектуальний вид спорту.
Анікєєв Юрій Володимирович
Випускник Куп’янської гімназії № 2
Міжнародний гросмейстер заслужений майстер спорту України, чемпіон світу по шашкам – 100
У 14 років став чемпіоном світу по шашкам - 64
У 16 років став чемпіоном Європи
У 33 роки став чемпіоном світу з Міжнародних шашок серед дорослих
У 35 років на чемпіонаті світу по шашкам – 64 завоював весь комплект нагород
1 місце у ІІ етапі Кубка світу 2019 з міжнародних шашок в Анталії.
3.2. Учитель. Переходимо до наступного етапу уроку "Аукціон задач". У кожного учня на парті знаходиться аркуш з умовами задач. Задачі різні.
Завдання для учнів.
1. Розв’язати одну задачу на вибір.
2. Пояснити, як пов’язані отримані відповіді з талановитими людьми Куп’янщини.
Задача 1. (середній рівень). Дано прямокутник АВСД, АВ = 5,5см, діагональ ВД утворює зі стороною АВ кут 60°. Знайти діагоналі прямокутника.
Задача 2. (достатній рівень). Дано ромб АВСД , ∠В = 120°, менша діагональ ВД = 
. Знайти більшу діагональ АС.
Задача 3. (високий рівень). Одна із сторін даху має форму рівнобічної трапеції. Сума верхньої і нижньої основ 20м, висота 3м, а бічна сторона нахилена до ніжної основи під кутом 45°. Знайти нижню основу.
Учитель. Як же пов’язані відповіді у задачах з талановитими людьми Куп’янщини.
Серія 5. Таланти Куп’янщини.
11 – Гутнік Ірина Валеріївна, керівник танцювального гуртка "Жар – птиця" на базі Куп'янської загальноосвітньої школи № 11.
Загальний танцювальний стаж нараховує з чоти річного віку.
30 – Гунченко Ніна Іванівна, понад 30 років співає у вокальному колективі "Слобожанка".
Працювала вчителем географії у ЗОШ №2, у 1991 році на серпневій конференції вчителів м. Куп’янська вперше виконала Державний Гімн України в дуеті із учителем української мови та літератури Паращич Ярославом Онуфрійовичем.
13 – Карєлкін Ілля учень 8 класу Куп’янської ЗОШ №4
"Учень 2020 року" Номінація "Митець року"
У свої 13 років зайняв ІІ місце у ХІІІ Міжнародному екологічному конкурсі "Метелики – німий шедевр природи" у номінації художня праця "Симетрія та романтизм у метелику зачаровані".
3.3. Учитель. Наступний етап уроку тестова самостійна робота по варіантах в режимі онлайн.
Завдання. Серед отриманих розв’язків у задачах знайти число, яке вказує вік учня, який навчався у Куп’янському НВК "Школа – гімназія №3", здобув звання Віце-Чемпіона Європи з карате у 2019 році.
Задачі І варіанту
1. Дано △АВС, ∠С = 90°, АВ = 5см, АС = 4см, СВ = 3см
Знайти синус кута А.
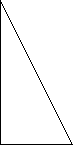А А) 0,6
Б) 0,8
4 5 В) 0,75
Г) 
С 3 В
Рис. 8
2. Дано △АВС, ∠С = 90°, АВ = 13см, СВ = 5см
Знайти АС.
А А) 12см
Б) 13см
? 13 В) 8см
Г) 17см
С 5 В
Рис. 9
3. З точки А, що знаходиться на відстані 8см від прямої а , проведено до неї дві похилі АВ і АС, які утворюють з прямою кути 30° і 45°. Знайти суму довжин похилих та їх проекцій.
А А) 
Б) 
В) 
В К С Г) 
Рис. 10
4. Спостерігачеві, який стоїть на висоті 50м, видно автомобіль під кутом 30° до горизонту (рис.11) Як знайти відстань від спостерігача до автомобіля ?
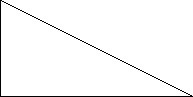
А D
50
30°
С В
Рис.11
А) 100м ; Б) 150м ; В) 50м ; Г) 200м.
Задачі ІІ варіанту
1. Дано △АВС, ∠С = 90°, АВ = 5см, АС = 4см, СВ = 3см
Знайти косинус кута А.
А А) 0,6
Б) 0,8
4 5 В) 0,75
Г)
С 3 В
Рис. 12
2. Дано △АВС, ∠С = 90°, АС = 12см, СВ = 5см
Знайти АВ.
А А) 12см
Б) 13см
12 ? В) 8см
Г) 17см
С 3 В
Рис. 13
3. З точки А, що знаходиться на відстані 6см від прямої а , проведено до неї дві похилі АВ і АС, які утворюють з прямою кути 30° і 60°. Знайти суму довжин похилих та їх проекцій.
А А) 
Б) 
В) 
В К С Г) 
Рис. 14
4. Ширина верхньої частини насипу шосейної дороги, поперечний переріз якого – рівнобічна трапеція, дорівнює 60м, відкоси 12м нахилені до горизонту, під кутом 60°. Знайдіть ширину нахилу у ніжній його частині ?
В С
12 А) 12м ; Б) 72м ;
В) 60м ; Г) 132м
А D
Рис. 15
Учитель. Число 16.
Серія 6. Спортивна гордість Куп’янщини 2020 року
Черняєв Олександр учень 11 класу Куп’янського НВК "Школа – гімназія №3"
Віце-Чемпіон Європи з карате
Це звання він здобув на спортивних змаганнях з карате у м.Анталія (Туреччина).
IV. "Китайська гра "чі – чао - чу"
Учитель. Основні етапи уроку закінчилися, наступив самий цікавий етап, це китайська гра "чі – чао – чу", що в перекладі означає танграм. Для проведення цієї гри я запрошую учня 8 класу (П.І.).
Виступ учня (про історію гри). Древні греки займалися геометрією, не тільки вимірюючи земельні ділянки і відстані до кораблів у морі. Вони любили геометричні ігри. Одна з них називається "стомахіон". В цій грі треба було з 14 частин квадрату скласти різні фігури. Цією грою захоплювалися настільки, що сам великий вчений Архімед написав про неї твір. Цією грою розважалися і древні китайці. Тільки вони ділили квадрат не на 14, а на 7 частин і, називали свою гру "чі – чао – чу", що означає "хитромудрий" орнамент з семи частин. Цю гру також називають "танграм". Цією грою захоплювався французький імператор Наполеон, який після військової поразки був зісланий на острів Святої Олени, де цілими годинами займався там складанням фігур танграма.
Завдання учням. Учні повинні скласти за 2 хв. квадрат із 7 частин.
Серія 7. Майстер головоломок
Борисов Сергій Віталійович
Працював вчителем хімії у Куп’янській гімназії № 2
За 30 секунд він склав квадрат із 7 частин.
V. Підсумок уроку.
VI. Домашнє завдання.
Повторити §3, п.18, № 624, творче завдання "Скласти прикладну задачу на розв’язування прямокутників".
про публікацію авторської розробки
Додати розробку