Презентація на тему "Додавання та множення числових нерівностей"
Про матеріал
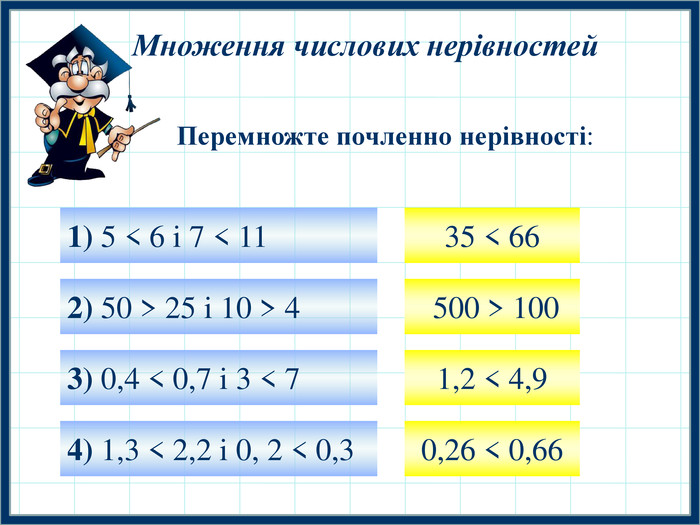
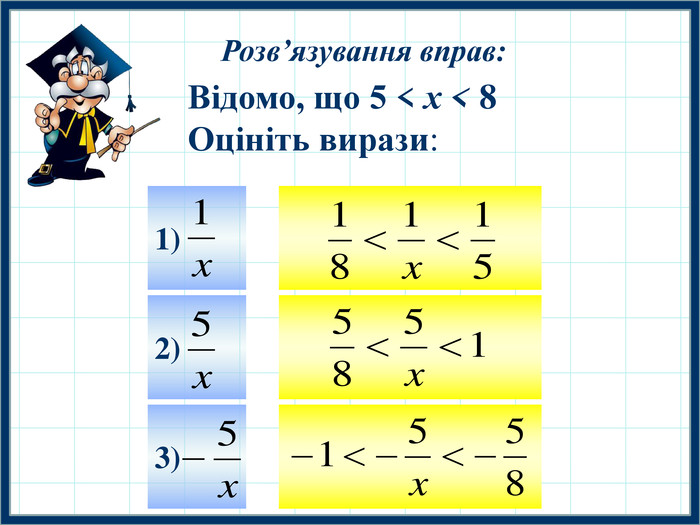
Презентація до уроку алгебри у 9 класі "Додавання і множення числових нерівностей , оцінювання значення виразів".На уроці вивчення властивостей нерівностей . а також демонстрація схеми додавання, множення , віднімання і ділення числових нерівностей. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Кравчук В.Р., Підручна М. В., Янченко Г. М.)
До уроку
3. Додавання і множення числових нерівностей. Оцінювання значень виразів Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
































-

Вигоднер Діана Ісаківна
18.09.2024 в 11:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Колесник Зоя
02.10.2023 в 20:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
28.09.2023 в 09:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Моісєєва Оксана Григорівна
25.09.2023 в 08:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Осадча Яна Анатоліївна
16.10.2022 в 16:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тиртишна Олена Іванівна
26.09.2022 в 21:27
Дякую!
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
22.09.2022 в 23:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Задорожна Олена Сергіївна
18.09.2022 в 13:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пінчук Людмила
08.09.2022 в 07:24
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Юріна Світлана
06.09.2022 в 13:04
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Недкова Алла Василівна
17.10.2021 в 21:27
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків