Презентація на тему "Дробові числа та дії з ними"
Про матеріал
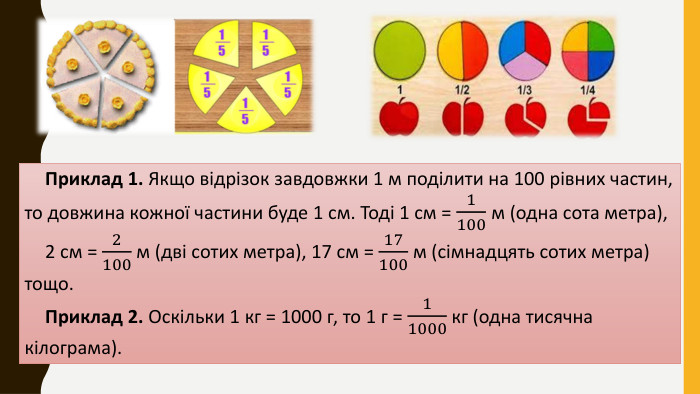
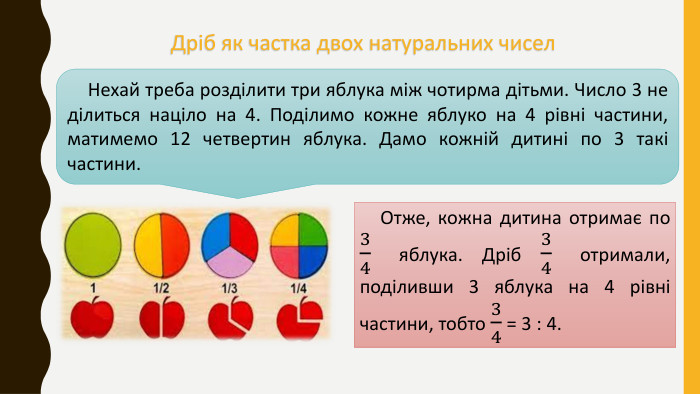
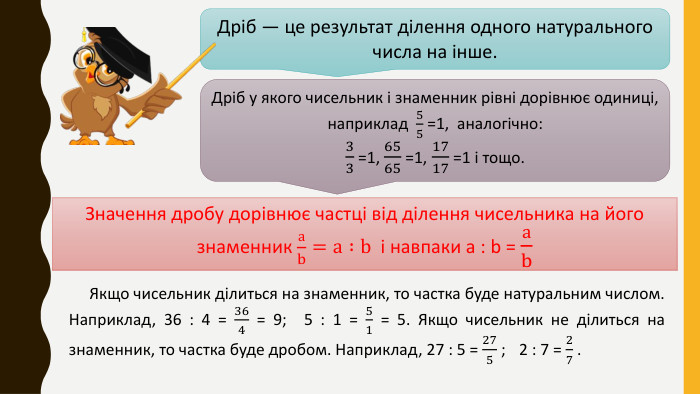
Дана презентація присвячена вивченню дробових чисел та основних арифметичних дій з ними. У матеріалі розглянуто поняття звичайних дробів, їх властивості, а також правила додавання, віднімання дробів. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку