Презентація на тему "Коло і круг"
Про матеріал
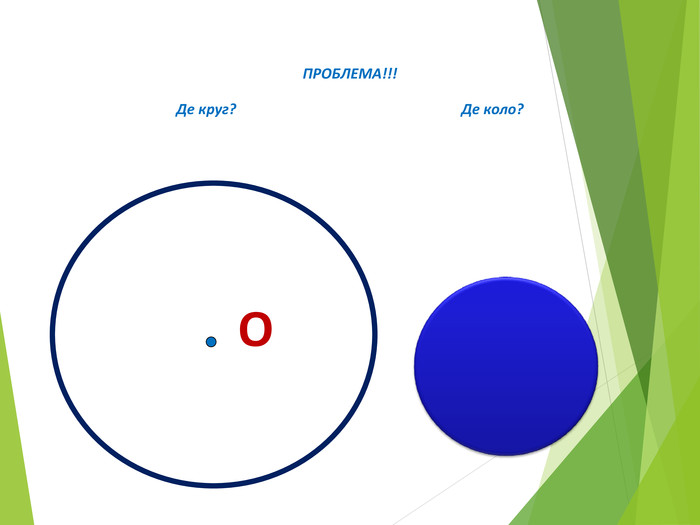
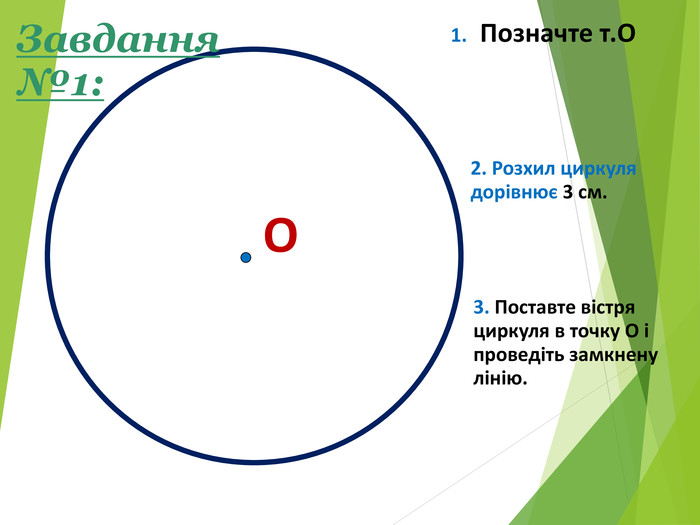
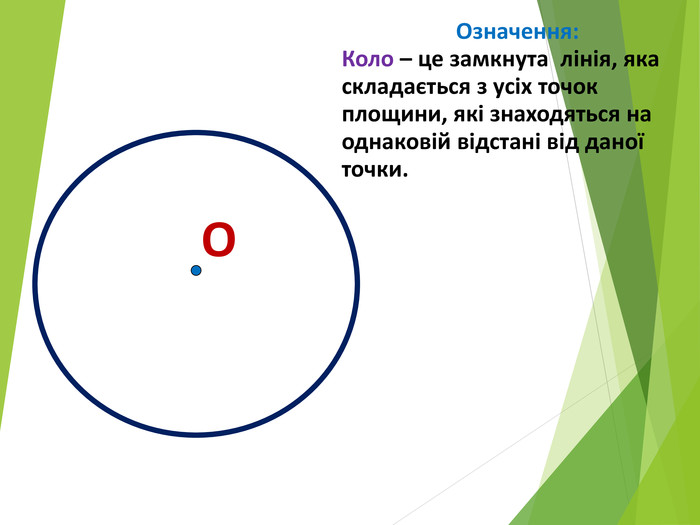
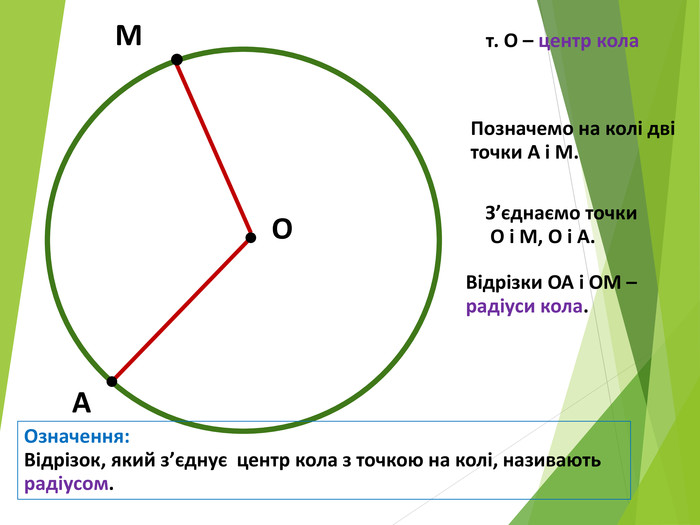
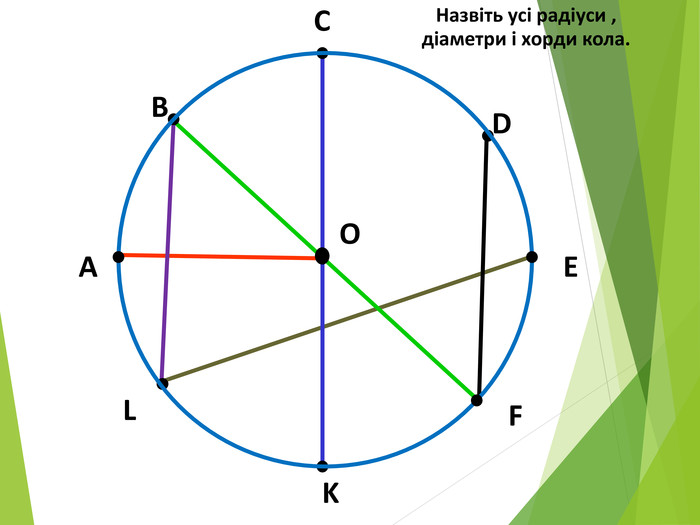
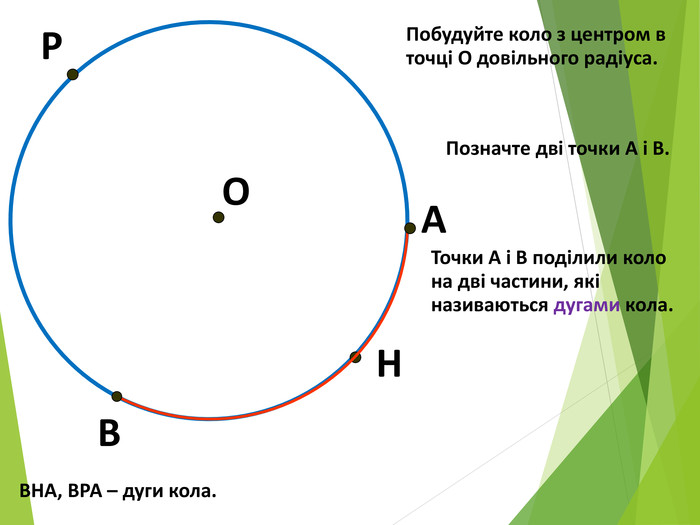
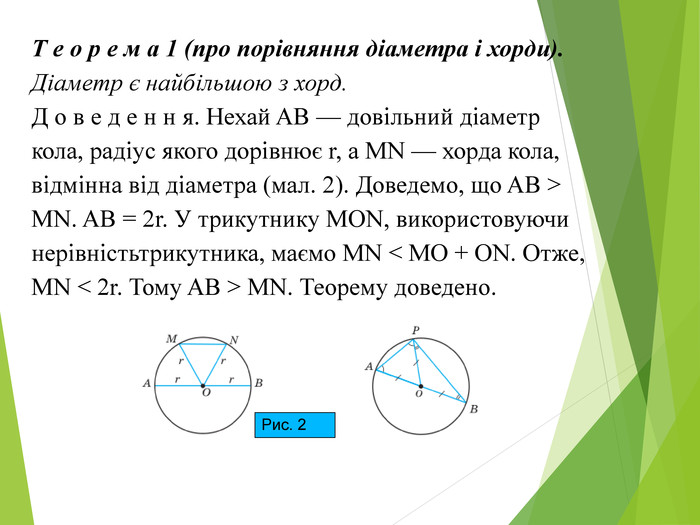
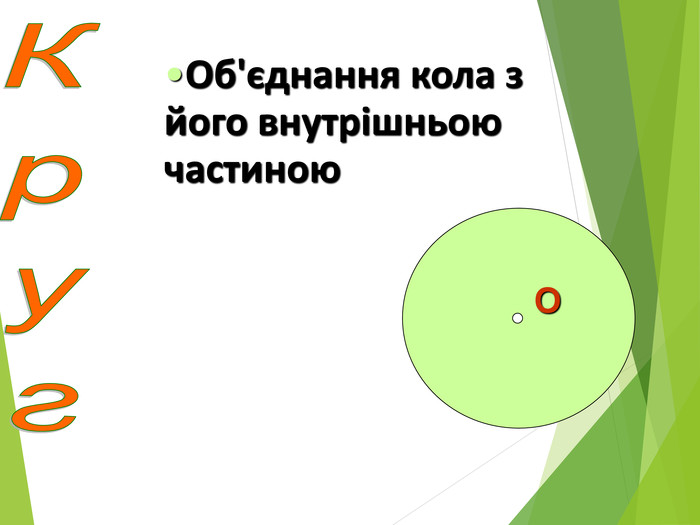
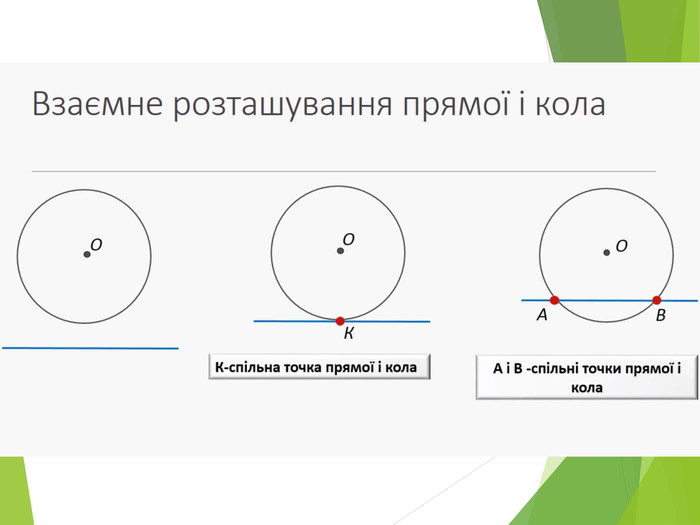
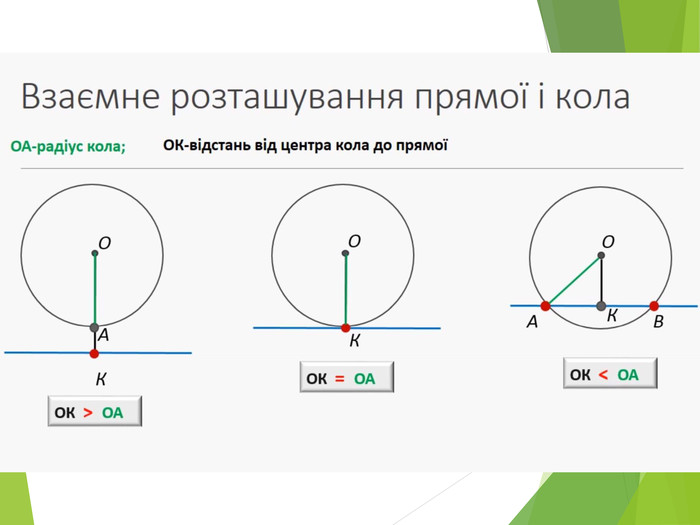
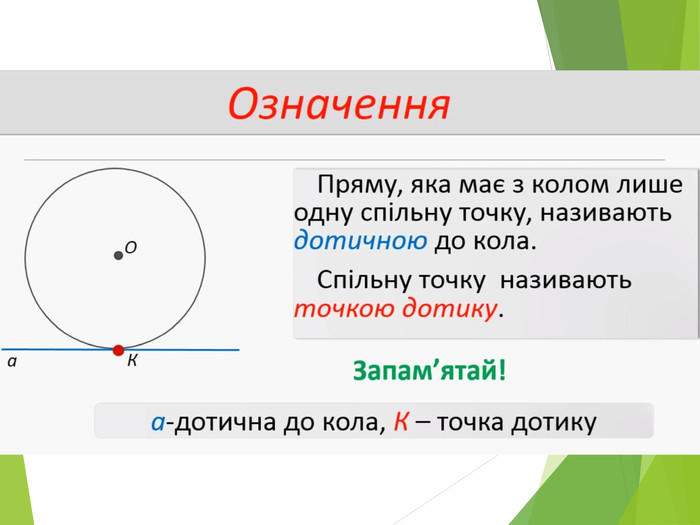
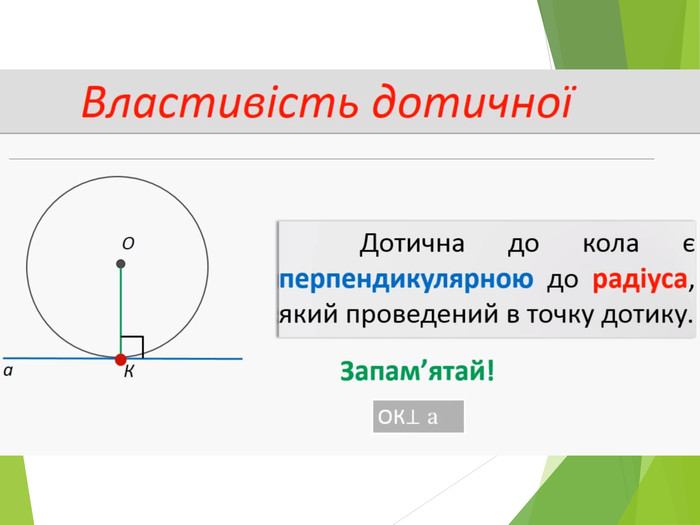
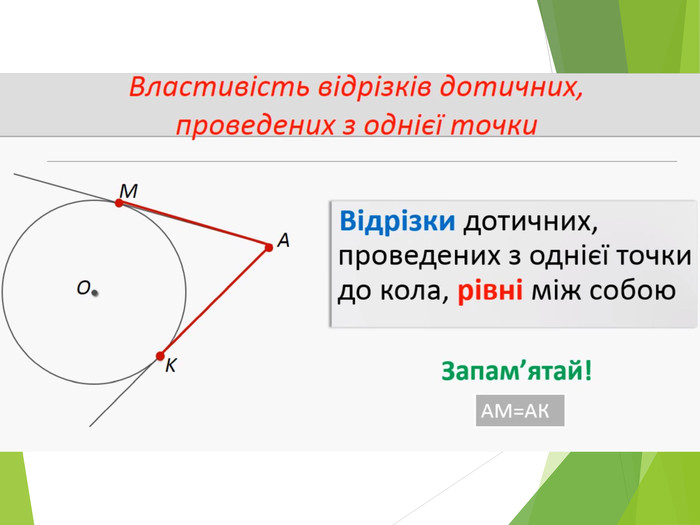
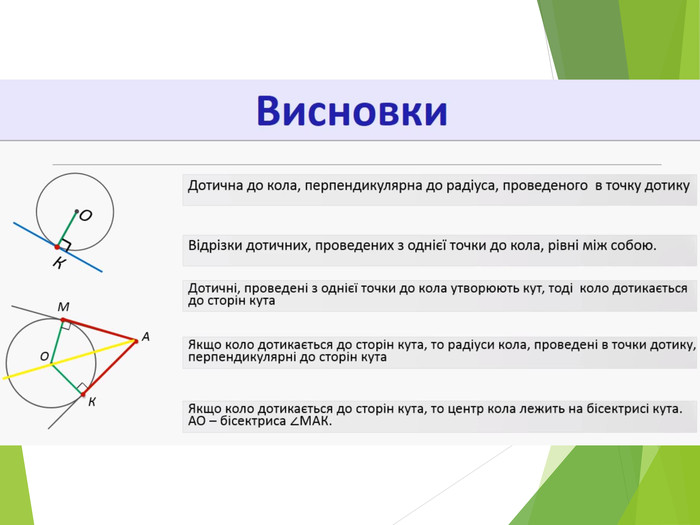
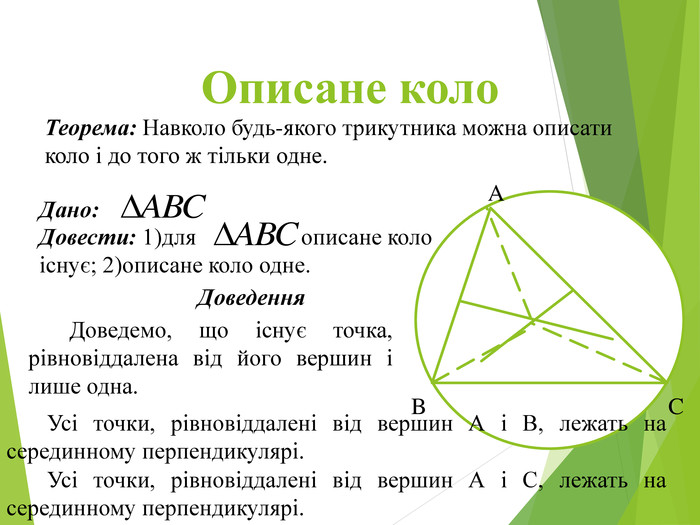
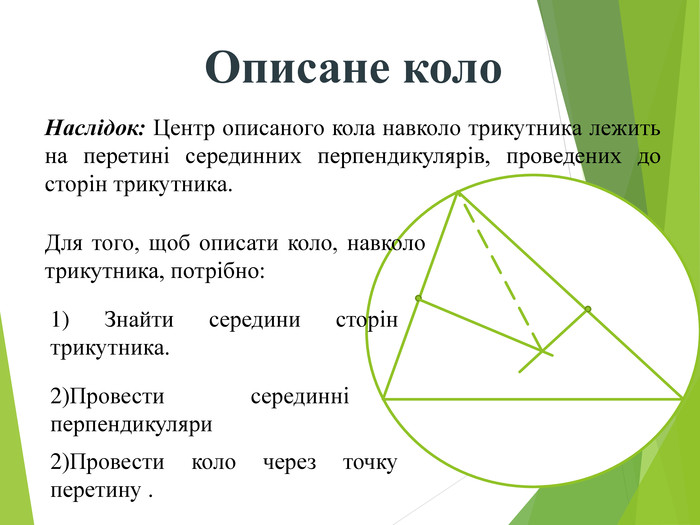
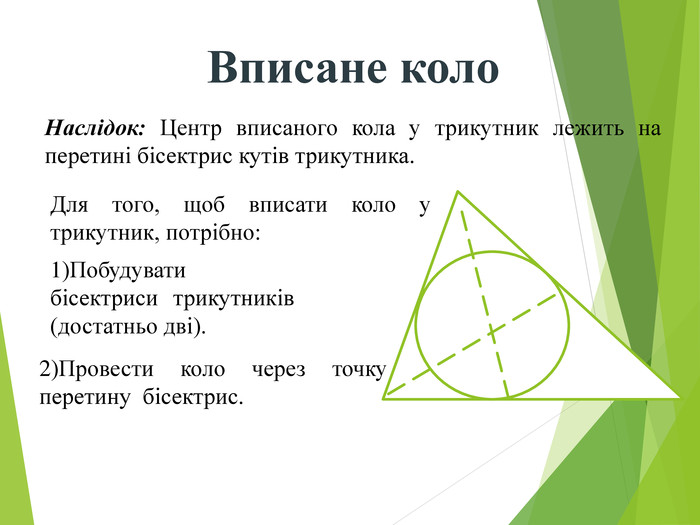
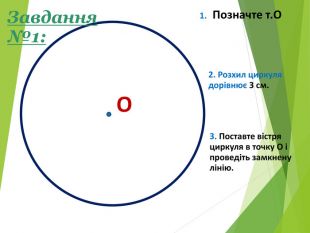
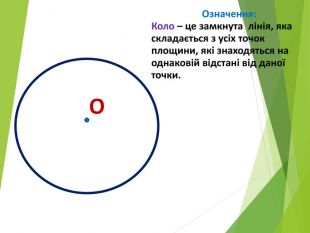
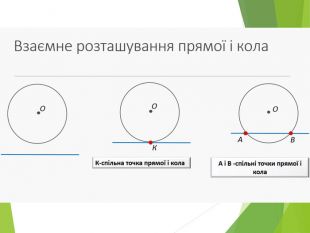
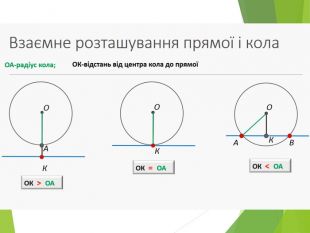
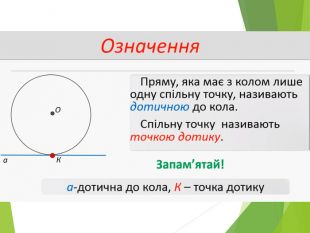
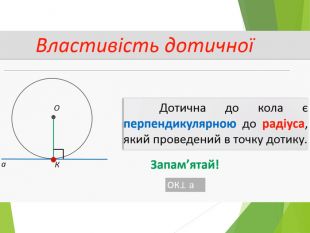
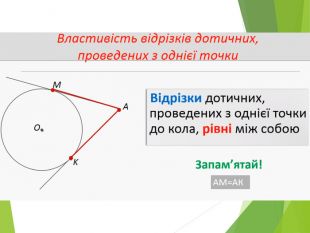
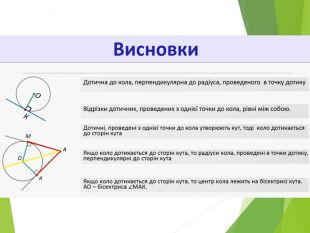
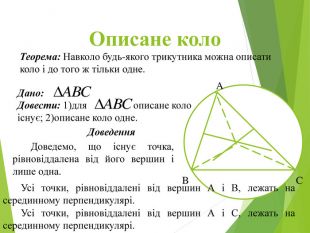
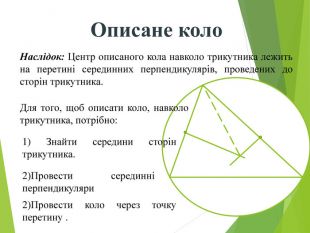
Засвоєння поняття кола, круга та їх елементів. Властивість діаметра, перпендикулярного до хорди. Дотична до кола. Властивість дотичної та відрізків дотичних . Коло, описане навколо трикутника. Коло вписане в трикутник. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




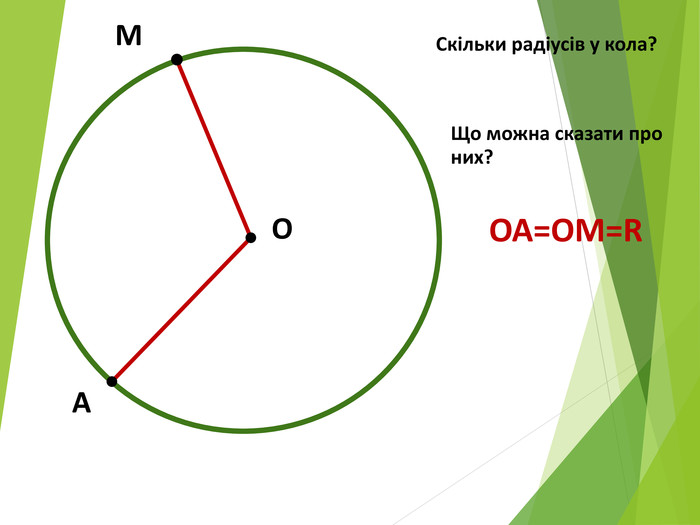
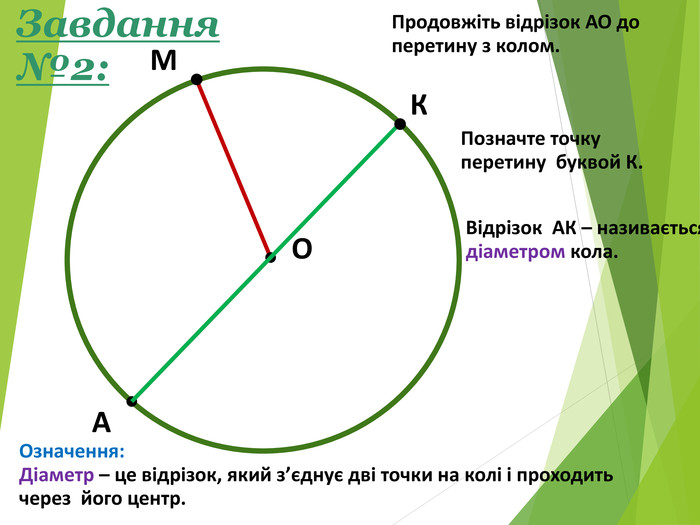
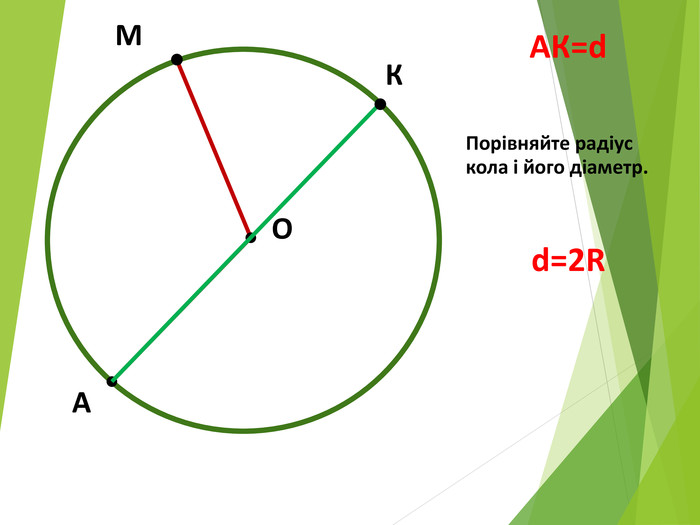
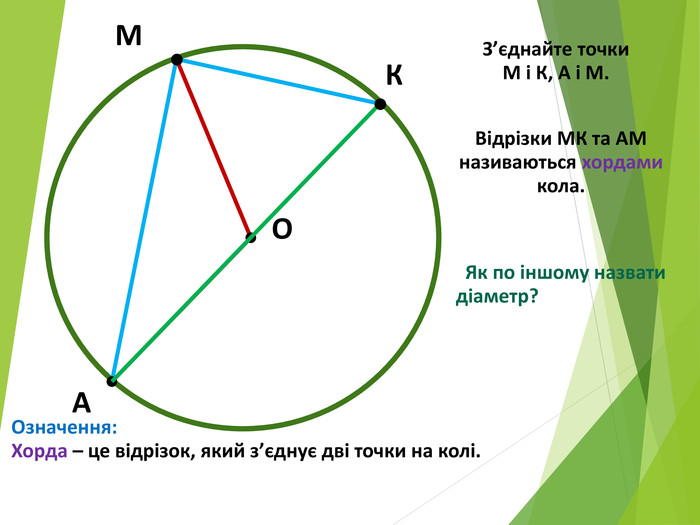






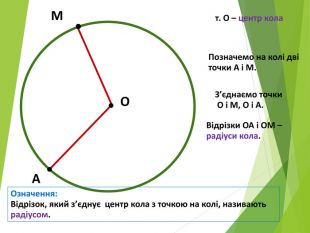
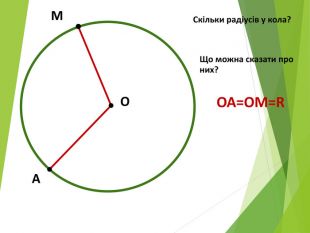
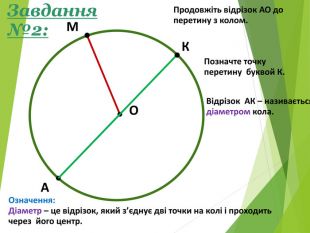
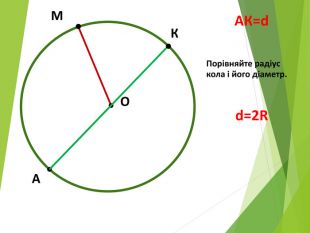
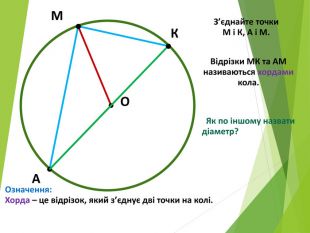
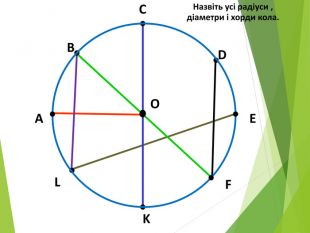
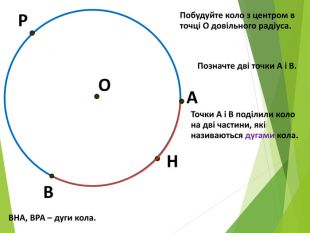

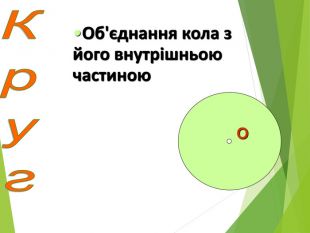




-

Лаптєва Інна
19.03.2024 в 13:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іменинник Людмила Миколаївна
28.02.2024 в 14:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
28.02.2024 в 00:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
09.04.2023 в 23:59
Для Підсумкового уроку супер!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самікова Ірина Олександрівна
04.02.2023 в 18:52
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Чусов Сергій Євгенович
07.11.2020 в 16:49
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Лампіка Ярина Ігорівна
29.04.2020 в 00:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука