Презентація на тему: "Площа криволінійної трапеції"

«Площа криволінійної трапеції»Тема заняття: Не достатньо знати, необхідно також застосовувати. Анатоль Франс

Мета заняття: Узагальнити і систематизувати знання студентів з теми «Визначені інтеграли»;Сприяти закріпленню знань про геометричний та фізичний зміст інтеграла; Навчити застосовувати математичні закони інтегрування в різних задачах;Розвивати творчі здібності, сприяти підвищенню інтересу до математики. Виховувати комунікативні риси, активність та спостережливість, вміння узагальнювати.

Перевірка домашнього завдання: Приклад 1. 70 Приклад 2. 39 Приклад 3.

“Несправний диктофон”Продовжіть речення, щоб сформульовані твердження були вірними:  «Невизначеним інтегралом називається …»                                 «Криволінійною трапецією називається…»«Дія, обернена до диференціювання …»«Первісні для однієї і тієї ж функції відрізняються тільки…» «Визначений інтеграл відрізняється від невизначеного тим, що…»«Функція записана  під знаком інтеграла, закінчується  знаками…» «Знак dx означає…»    

Завдання. Заповнити таблицю первісних.{775 DCB02-9 BB8-47 FD-8907-85 C794 F793 BA}f(x)x2sin xcos xхх -23х2 F(x)lnǀxǀ+C5х+Сtg x + C+С

Відповіді{775 DCB02-9 BB8-47 FD-8907-85 C794 F793 BA}f(x)x25sin xcos xхaxх -23х2 F(x)+Сlnǀxǀ+C5х+С-cosx+CSinx+Ctg x +C+C+С+Cx3+C

Історична подорож.

«Інтеграл» - латинське слово integro – “відновлювати” або integer – “цілий”. Одне з основних понять математичного аналізу, що виникло у зв’язку з потребою виміряти площі, об’єми, шукати функції за їхніми похідними. Вперше це слово використав в друку швецький вчений Якоб Бернуллі (1690 г.)

Знак ∫ - стилізована літера S від латинського слова summa – “сумма”. Вперше з’явився у Готфріда В. Лейбница в 1686 р.

Німецький філософ і математик1646 - 1716 гг. Готфрид Лейбніц

Німецький філософ, математик, фізик та мовник. Він і англійський вчений І. Ньютон створили (незалежно один від одного) основи важливого розділу математики – математичного аналізу. Лейбніц ввів багато понять та символів, що застосовуються в математиці і зараз, зокрема, він ввів термін “функція”. ГОТФРИД ВІЛЬГЕЛЬМ ЛЕЙБНІЦ

Будинок, в якому мешкав Г. В. Лейбніц

Життя і діяльність Ісаака Ньютона

Ісаак Ньютон. Народився:04.01.1643, Вулсторп (біля Грантема)Помер:31.03.1727,Кенсингтон (нині частина Лондона)

Ісаак НьютонІсаак Ньютон - великий англійський фізик, механик, астроном и математик. Один із засновників сучасного природознавства. Член Лондонского королівскої общини (1672), його президент (з 1703) ppt_xxshearppt_x

Основні віхи життя. Батько Ньютона помер невдовзі до народження сина. В 12 років Ньютон почав навчання у школі в Грантемі, в 19 років поступив на навчання до Трініті-колледж   Кембриджского університету, який закінчив в 22 роки із ступенем бакалавра. В 1668 отримав ступінь магістра. В 1669-1701 очолював фізико-математичну кафедру Кембриджского університету. В 1695 був призначений наглядачем, в 1699 - директором Монетного двору, де провів велику работу по перекарбуванню монети, привів у порядок монетну справу в Англії. ppt_xxshearppt_x

ПраціНайбільша праця Ньютона "Математичні початки натуральної філософії» (скорочено «Початки») - був виданий в 1687. У «Початках» дане формулювання основних понять і принципів механіки у вигляді трьох відомих законів - закон інерції, закон зміни кількості руху пропорціного прикладенній силі, закон рівності дії та притидії. На їх основі Ньютон вивів закони руху тіл у полі центральних сил не тільки в вакуумі, а й в середовищі. ppt_xxshearppt_x

Ісаак Ньютон«Оптика»Ньютон написав фундаментальну працю «Оптика» (1704). У ній він показав, що за допомогою скляної призми можна розкласти білий світ на промені різних кольорів з різним ступенем преломляемості, и пояснив цим хроматичну аберацію лінз. Помилково вважаючи цю аберацію невід'ємною, створив в 1668 і 1671 телескопи-рефлектори, засновані на явищі відбиття світлових променів від угнутого дзеркала.

Відкриття. В результаті дослідів Ньютона по розкладанню білого світла призмою стало можливим відкриття в 1859 Г. Р. Кірхгофом і Р. В. Бунзеном одного з основних методів дослідження в астрофізиці. Відкриття Ньютона властивостей світла були фундаментальними для оптики і в кінцевому рахунку привели до розуміння природи (зображення) в телескопі. Від першого маленького відбивного телескопа Ньютона була прокладена широка дорога до потужних рефлекторів нашого часу. Нарешті, від ньютонівської механіки і теорії всесвітнього тяжіння був здійснений перехід до релятивістської механіки. Внесок Ньютона в природознавство назавжди увійшов до скарбниці людського розуму. Ньютон помер у Кенсінгтоні (нині частина Лондона) і похований у Вестмінстерському абатстві.

Ісаак Ньютон. ПраціНьютон є завновником математичних непреривних процесів. Розробив одночасно с Г. В. Лейбніцем основи диференційного і інтегрального обчислень. Займався алгеброю, аналітичної геометрією, поставив ряд проблем варіаційного числення. ppt_xxshearppt_x

Його ім’я занесено на карту Місяця і Марса

Застосування визначеного інтеграла

Застосування визначеного інтеграла. ВИЩА МАТЕМАТИКАЕНЕРГЕТИКАБІОЛОГІЯМАТЕМАТИКАЕКОНОМІКАФІЗИКА

Математика. Для обчислення площ та об’ємів

Площа криволінійної трапеції розраховується за формулою:аву=f(x)0хy

Завдання.

Якщо фігура обмежена графіками двох функцій, при g(х)>f(х), тоу=f(х)0хyу=g(х)ab

Завдання.

Фізика. Для визначення: Кількості теплоти; електричного заряда; маси, переміщення; роботи, витраченої на розтягування або стисткання пружини; шляху, пройденого тілом.

Обчислення шляху за відомим законом зміни швидкості.

Розв'яжемо задачу: Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом v=2t+1(м/с). Знайти шлях, який пройшло тіло за інтервал часу від t 1 =1c, до t2 =3c.

ІНТЕГРАЛ В ЕКОНОМІЦІЗагальний прибуток за час t1 можна знайти за формулою:

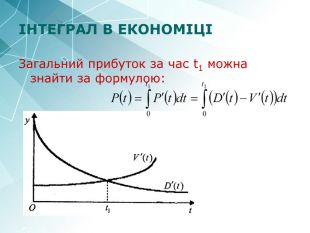
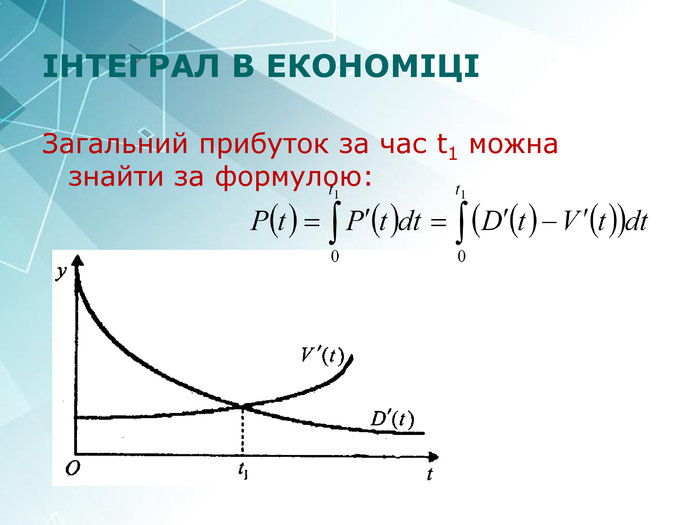
Приклад 1.  Експериментально встановлено, що продуктивність праці робітника наближено виражається формулоюf(t)= -0.0033t2 - 0.089t + 20.96, де t — робочий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним. . Протягом кварталу обсяг випуску продукції становитиме: Відповідь: Од.

ІНТЕГРАЛ В ПОБУТІЩоб каша була смачною, потрібно таке відношення води і круп:

РОБОТА В ГРУПАХФінансисти. АрхеологиІнженери. Енергетики

ФІНАНСИСТИНа полі пшениці після приземлення космічного корабля  залишився  слід, який нагадує фігуру, обмежену лініями у =‌‌‌‌‌ –х2 + 9 та у = х2 + 1. Необхідно визначити збитки, заподіяні агрокомплексу, якщо з 1 м2 отримують в середньому 3,8 кг пшениці, яка коштує  0,8 грн. / кг.

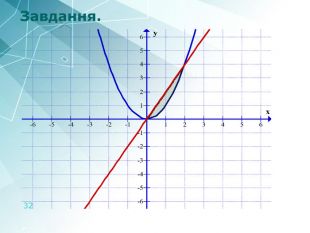
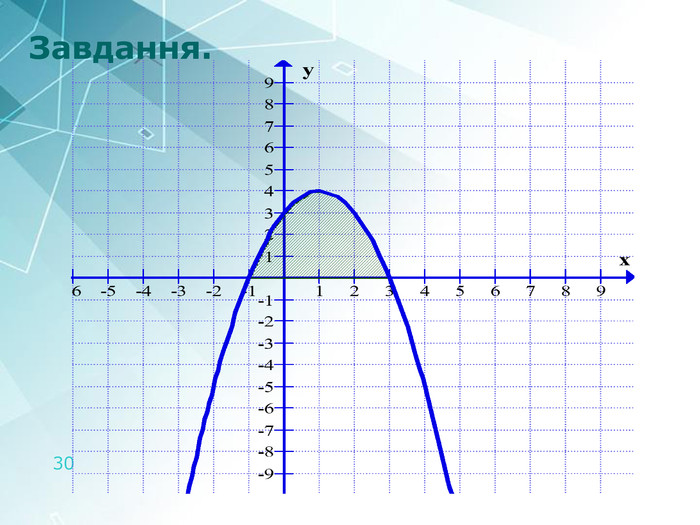
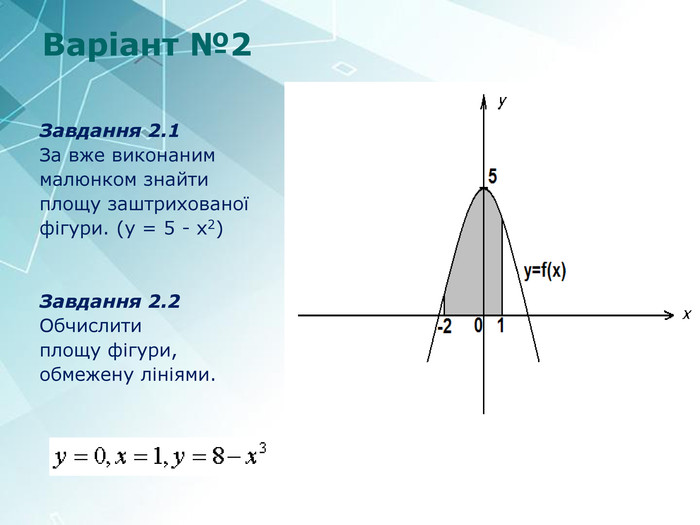
АРХЕОЛОГИНещодавно археологи при дослідженні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після було з’ясовано, що це місце мало форму, схожу на фігуру, утворену параболою у = –  х2 + 2х + 3 і віссю Ох (х вчені вимірювали в метрах). Обчислити площу жертовного місця, виконайте малюнок.

ІНЖЕНЕРИДля кращого обслуговування заїзду гонок серії « Формула-1» майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t)=3t2+2t . Який шлях проїде пілот цієї гонки з 2-ої до 7-ої секунди від початку руху? Одиниці виміру м. Виконайте малюнок.

ЕНЕРГЕТИКИНавантаження  на Криворізьку теплоелектростанцію задається функцією   f(x) = 3x2 + 4x – 2. Визначити витрати електроенергії протягом доби. Одиниці виміру к. Вт/год. Намалюйте графік.

"Забути не можна пам’ятати!"

Варіант №1 Завдання 1.1 За вже виконаниммалюнком знайти площу заштрихованоїфігури. (у = х2+2)  Завдання 1.2 Обчислити площу фігури, обмежену лініями.

Завдання 1.1 S = 9. Варіант №1. Завдання 1.2 S = Варіант №2. Завдання 2.1 S = 12. Завдання 1.2 S =

Варіант №2 Завдання 2.1 За вже виконаниммалюнком знайти площу заштрихованоїфігури. (у = 5 - х2) Завдання 2.2 Обчислити площу фігури, обмежену лініями.

Домашнє завдання. 1. Повторити методи, що застосовуються при обчисленнї площі криволінійної трапеції.2. Виконати завдання с. 119, № 530 а), б).