Презентація на тему "Правильні багатогранники. Види багатогранників"

Тема уроку. Правильні багатогранники.

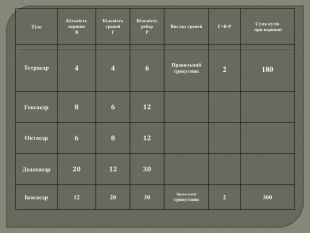
Математичний диктант «Вірю – не вірю»«+» - вірю, « -» - не вірю. Всі бічні грані піраміди - трикутники Висота прямої призми дорівнює її висотіТрикутна піраміда має 4 граніАпофема правильної піраміди довша за її висоту. П’ятикутна призма має 15 ребер. Бічні грані правильної піраміди – рівнобедрені трикутники. Бічні грані зрізаної піраміди – паралелограми. Чотирикутна призма має 4 граніОснови призми рівні і паралельніБудь-яка грань призми – паралелограм. Бічне ребро піраміди може дорівнювати висотіТрикутна призма має 6 вершин.

Оцінювання: 1 бал-правильна відповідь(+) Всі бічні грані піраміди - трикутники (+) Висота прямої призми дорівнює її висоті(+) Трикутна піраміда має 4 грані(+) Апофема правильної піраміди довша за її висоту(+) П’ятикутна призма має 15 ребер(+) Бічні грані правильної піраміди – рівнобедрені трикутники(-) Бічні грані зрізаної піраміди – паралелограми(-) Чотирикутна призма має 4 грані(+) Основи призми рівні і паралельні(-) Будь-яка грань призми – паралелограм(+) Бічне ребро піраміди може дорівнювати висоті(+) Трикутна призма має 6 вершин.

«Немає жодної галузі математики, якою б абстрактною вона не була, що коли-небудь не виявиться застосованою для явищ дійсного світу» М.І. Лобачевский

Мета уроку: сформувати поняття про правильні многогранники; ознайомити з видами правильних многогранників та їх властивостями

Опуклий багатогранник називається правильним, якщо його грані є правильними многокутниками з однією і тією самою кількістю сторін, а в кожній вершині многогранника сходиться одне і те ж число ребер

Правильних багатогранників всього п’ять, але Льюіс Керролл так сказав про них: «Правильних багатогранників до неподобства дуже мало, але цей досить скромний по чисельності загін зумів пробратися в самі глибини різних наук».  

Назва багатогранника  І частина ІІ частина«тетра» - 4 «едра» - грань«гекса» - 6 «окта» - 8«додека »-12«ікоса» - 20

Правильний тетраедр – це многогранник, у якого всі грані – правильні трикутники і в кожній вершині сходиться по 3 ребра. Елементи: Вершин – 4 Ребер – 6 Граней – 4

Гексаедр (куб) – це багатогранник, у якого всі грані квадрати і в кожній вершині сходиться по три ребра Елементи: Вершин – 8 Ребер – 12 Граней – 6

Октаедр – це багатогранник, у якого всі грані правильні трикутники і в кожній вершині сходиться по чотири ребра Елементи: Вершин – 6 Ребер – 12 Граней – 8

Додекаедр – це багатогранник, у якого всі грані правильні п’ятикутники і в кожній вершині сходиться по три ребра Елементи: Вершин – 20 Ребер – 30 Граней – 12

Ікосаедр – це багатогранник, у якого всі грані правильні трикутники і в кожній вершині сходиться по п’ять ребер Елементи: Вершин – 12 Ребер – 30 Граней – 20

Тіло. Кількість вершин. ВКількість граней. ГКількість ребер. РВигляд граней. Г+В-РСума кутів при вершиніТетраедр446 Правильний трикутник2180 Гексаедр8612 Октаедр6812 Додекаедр201230Ікосаедр122030 Правильний трикутник2300

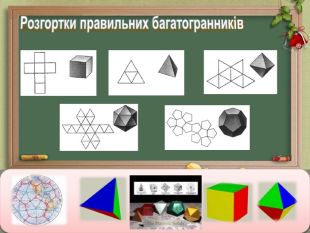
У своїх філософських теоріях правильні багатогранники застосовували багато вчених. Ще в Древній Греції були описані всі правильні багатогранники. Особливо важливе місце багатоогранникам приділяли піфагорійці – учні школи Піфагора (VI – V століття до н.е.), де устрій світу тісно зв'язувався з геометрією, геометричним тілами.

 Для будь-якого опуклого багатогранника справедливе співвідношення: Г+ В – Р = 2, де Г – кількість граней, В – кількість вершин, Р – кількість ребер Теорема Ейлера

Основні властивості правильних багатогранників:всій грані рівні правильні багатогранники всі плоскі кути рівні всі двогранні кути, що містять дві грані із загальним ребром, рівні всі ребра рівні, всі багатогранні кути рівні, у кожній вершині сходиться однакова кількість ребер

 Розгортки правильних багатогранників

Г=12, В=10, Р=20, Г+В-Р=212+10-20=2

r

Задача 3 Довжина ребра октаедра дорівнює 6 см. Знайдіть площу його повної поверхні.

Задача 4 Знайдіть суму всіх плоских кутів ікосаедра

Історія. У давні часи геометричним фігурам, особливо правильним, надавали таємничого філософського змісту. Так, за Платоном, усе в природі створено взаємодією повітря, води, землі, і вони мають відповідні форми: тетраедра, октаедра, ікосаедра, додекаедра, гексаедра

Земля. Вода. Всесвіт. Вогонь. Повітря

 Тетраедр - вогонь

 Гексаедр - земля

 Октаедр - повітря

 Ікосаедр - вода

 Додекаедр - всесвіт. Платон: «Його Бог визначив для Всесвіту й удався до нього, коли розмальовував його й прикрашав»

 Правильні багатогранники в мистецтві“ Таємна вечеря ” С. ДаліНа картині Христос зі своїми учнями зображений на фоні величезного прозорого додекаедра. Форму додекаедра, як вважали раніше, мав ВСЕСВІТ, тобто вважалось, що ми живемо всередині зводу, який має форму поверхні правильного додекаедра

 Правильні багатогранники в природіНімецький біолог початку ХХ ст. Еге Геккель дослідив, що скелет одноклітинного організму феодарії за формою нагадує ікосаедр .

Математика володіє не тільки істиною, а й вищою красою – красою відточеною й точною, піднесено чистою, яка наближається до справжньої досконалості, що властива лише найвеличнішим зразкам мистецтва Бертран Рассел

 Правильні багатогранники в мистецтві“Меланхолія” А. Дюрер. На картині – “Меланхолія” Дюрера, це гравюра 16-го століття, зображено неправильний багатогранник, який тримає композицію й зрівноважує фон

 Титульна сторінкакниги Ж. Кузена. Надгробний пам’ятник в Солсбері

Репродукція літографії Ешера (1943) “ Рептилії ” – все тримається на додекаедрі Правильні багатогранники в мистецтві“Меланхолія” А. Дюрер

 Платон, Евклід, Архімед і Кеплер використовували в своїх філософських теоріях правильні багатогранники.

Висновки  Судячи з усього, правильні багатогранники будуть відігравати все важливішу роль у різних галузях знань, адже ці фігури внутрішньо пов’язані з природними явищами. Як говорив Платон, із усіх відомих тіл вони найпрекрасніші, причому кожен багатогранник прекрасний по-своєму. Мабуть,це той випадок, коли краса та істина — єдине ціле