Презентація на тему «Розв язування вправ на всі дії з раціональними числами»
Про матеріал
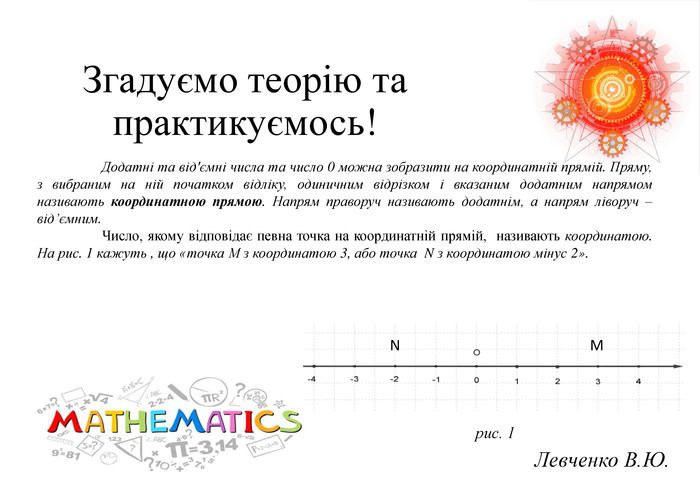
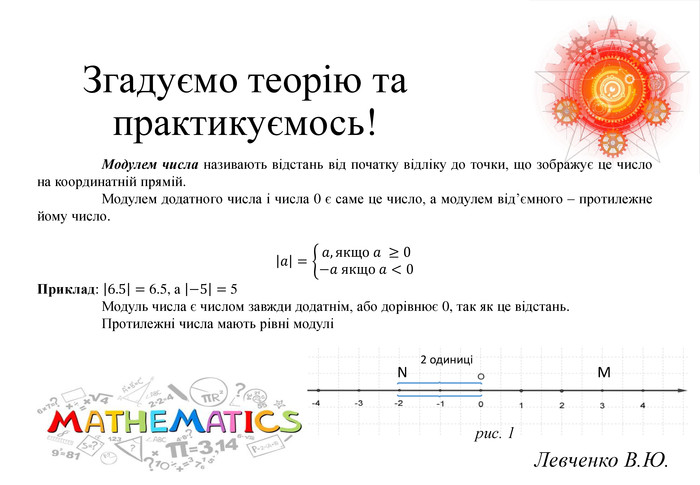
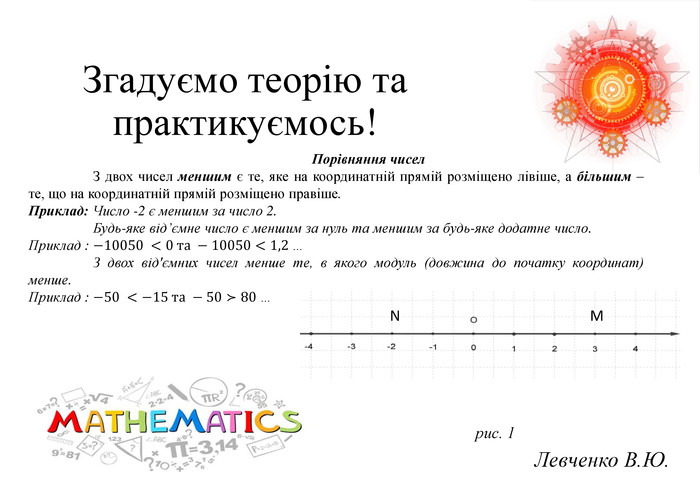
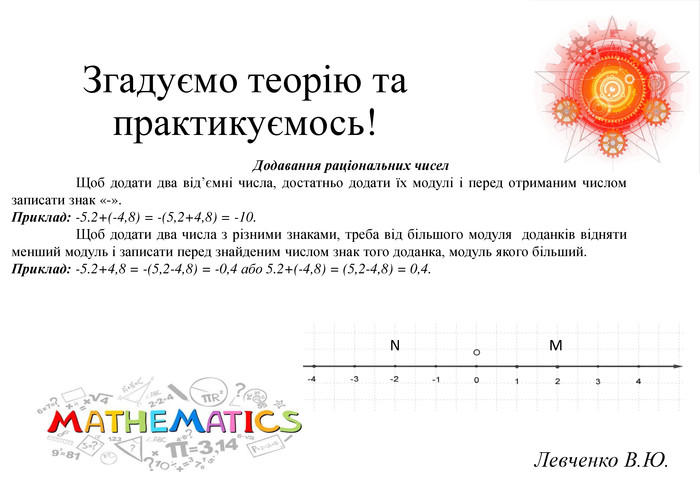
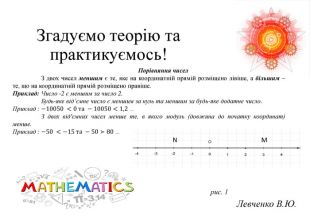
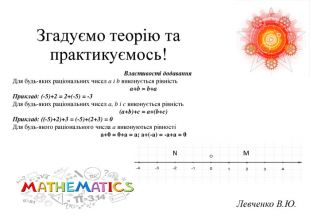
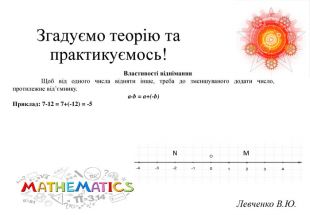
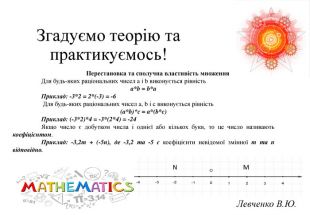
Презентація на тему «Розв язування вправ на всі дії з раціональними числами» допоможе учням систематизувати свої знання, отримані під час вивчення розділу "Раціональні числа та дії над ними". Також в презентації міститься слайд з типовими помилками, що допускають учні під час роботи з даною темою та поради до їх вирішення.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку