Презентація на тему "Теорема Піфагора" для 8 класу

Теорема Піфагора Навчальний проект Турко О.Г., вчитель математики вищої категорії, вчитель-методист

Теорема Піфагора У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи а c b a2 + b2 = с2

Стародавня індійська задача Бхаскари Квітка лотоса при вертикальному положенні стебла піднімалася над водою на Ѕ фута. Вітер відхилив її на 2 фути від попереднього положення (по поверхні води). Після цього квітка лотоса опинилася на рівні води. Визначте глибину озера в цьому місці. (Х + Ѕ)2 – X2 = 22 X 2 + X + ј - X 2 = 4 X = 3 ѕ (футів) – глибина озера х х + Ѕ 2 А В С К

“Палка довжиною 1/2, приставлена до стіни. Її верхній кінець опустили на 1/10. Як далеко відсунеться її нижній кінець ?” У давньому Вавилоні властивість не тільки трикутника зі сторонами 3, 4, 5, але й узагалі всіх прямокутних трикутників була добре відома. Так, в одному з найбільш давніх вавилонських математичних текстів є дуже цікава задача: с b У задачі, як бачимо, за даними гіпотенузи с = 1/2 та одного з катетів b = 1/2 - 1/10 = 2/5 необхідно знайти другий катет. Його вавилоняни знаходять “по Піфагору": а2 = с2 - в2 а = √ 1/4 - 4/25 а = 3/10 ?

Старовинні задачі : Случися некоему человеку к стене лествицу прибрати, у стены же тоя высота есть 117 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать. 1252 = 1172 + Х2 X2 = 1252 – 1172 X2 = (125 – 117)(125 + 117) X = 44(стопи) – на такій відстані нижній кінець драбини знаходиться від стіни. Задача з першого підручника математики на Русі під назвою “Арифметика” Леонтія Пилиповича Магницького.

      Доведення теореми вважалося дуже важким і мало назву “Dons asinorum” - “міст віслюка” або “elefuga” - “втеча вбогих” , “вітряний млин” “теорема-метелик” або “теорема нареченої” а сама теорема –

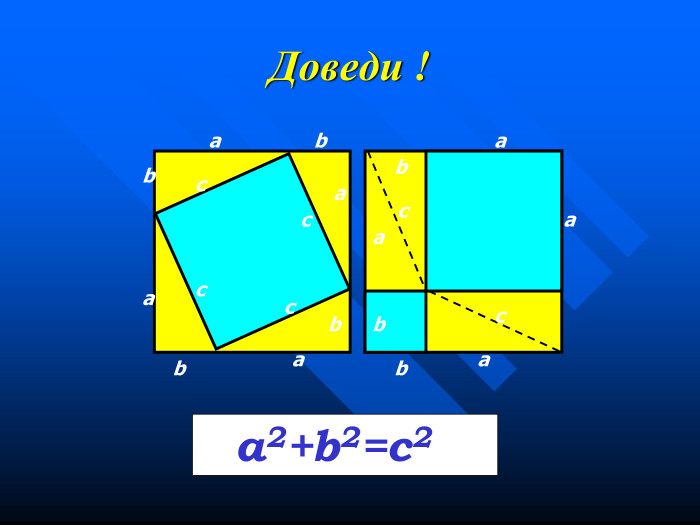
ДАВНЬОІНДІЙСЬКЕ ДОВЕДЕННЯ У математичних трактатах Давньої Індії, доводячи теорему, часто наводили тільки малюнок і супроводжували його лише одним словом: “Дивись !” “Наскільки багатообіцяюча область знань і які незліченні варіації можуть бути у відповідях на одне і те ж питання” Лев Толстой

Доведи ! а а а а а а а а b b b b b b b с с с с с с а2+b2=с2

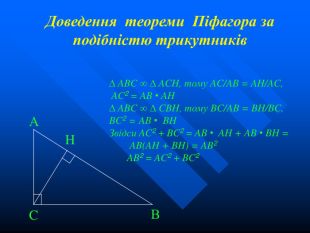
a b c α β Доведення : Нехай маємо довільний прямокутний трикутник з катетами а,b і гіпотенузою с. На кожній стороні квадрата зі стороною с добудуємо трикутник. Утвориться квадрат зі стороною (а+в). Sкв. = (a + b) 2 або Sкв. = 4Sтр. + S`кв. Sтр. = 1/2ab; S`кв. = c 2, тоді Sкв. = 4 • 1/2ab + c 2 Тобто : (a + b) 2 = 4 • 1/2ab + c 2 a 2 + 2ab + b 2 = 2ab + c 2 a 2 + b 2 = c 2 a b c α β a b с α β a b c α β

(з інших джерел, більше п’ятисот ), але жага до примноження їх кількості збереглася, тому теорему Піфагора занесено в “Книгу рекордів Гінеса”. Самостійне “відкриття” доведення теореми Піфагора буде корисним і сучасним учням Спробуй доведи З глибокої давнини математики знаходять усе нові й нові доведення теореми Піфагора , усе нові й нові задуми її доведень. Таких доведень – більш менш суворих, більш менш показових – відомо більше півтори сотні

Доведення теореми Піфагора за подібністю трикутників A C H В ∆ ABC ∞ ∆ ACH, тому AC/AB = AH/AC, AC2 = AB • AH ∆ ABC ∞ ∆ CBH, тому BC/AB = BH/BC, BC2 = AB • BH Звідси AC2 + BC2 = AB • AH + AB • BH = AB(AH + BH) = AB2 AB2 = AC2 + BC2

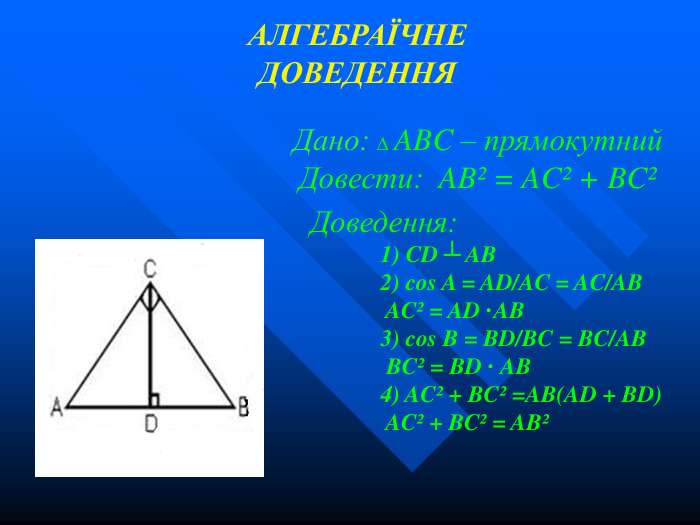
Доведення: 1) добудуємо відрізок CD = AB; проведемо ED ┴ AD ;ED = AB 2) SABED = S∆ABC + S∆CDE + S∆BCE SABED = 2 • AB • AC • 1⁄ 2 + 1⁄ 2 BC2 SABED = (DE + AB) • AD • 1⁄ 2 AB • AC + 1⁄ 2 BC2 = 1⁄ 2 (DE + AB) • AD AB • AC + 1⁄ 2 BC2 = 1⁄ 2 (DE + AB)(CD + AC) AB • AC + 1⁄ 2 BC2 = 1⁄ 2 (AC + AB)2 AB • AC + 1⁄ 2 BC2 = 1⁄ 2 AC 2 + AС • АВ + ⁄ 2 АB 2 BC2 = AC 2 + АB 2 ГЕОМЕТРИЧНЕ ДОВЕДЕННЯ Дано: ∆ ABC – прямокутний трикутник Довести BC2 = AB2 + AC2

Доведення: 1) CD ┴ AB 2) cos A = AD/AC = AC/AB ACІ = AD ·AB 3) cos B = BD/BC = BC/AB BCІ = BD · AB 4) ACІ + BCІ =AB(AD + BD) ACІ + BCІ = ABІ АЛГЕБРАЇЧНЕ ДОВЕДЕННЯ Дано: ∆ ABC – прямокутний Довести: ABІ = ACІ + BCІ

Доведення Эвкліда

Дано: ∆АВС – прямокутний а = ВС – катет в = АС – катет, с = АВ – гіпотенуза. A B C с S = c2 в S = в2 a S = a2 Довести : с2 = а2 + в2 або АВ2 = АС2 + ВС2 Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на його катетах.

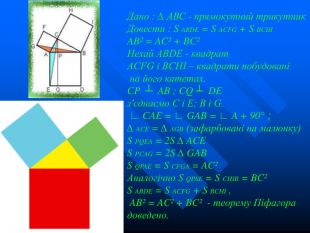
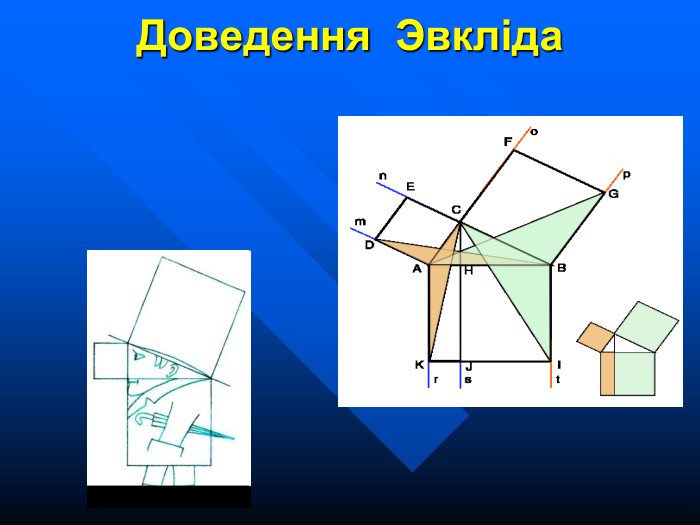
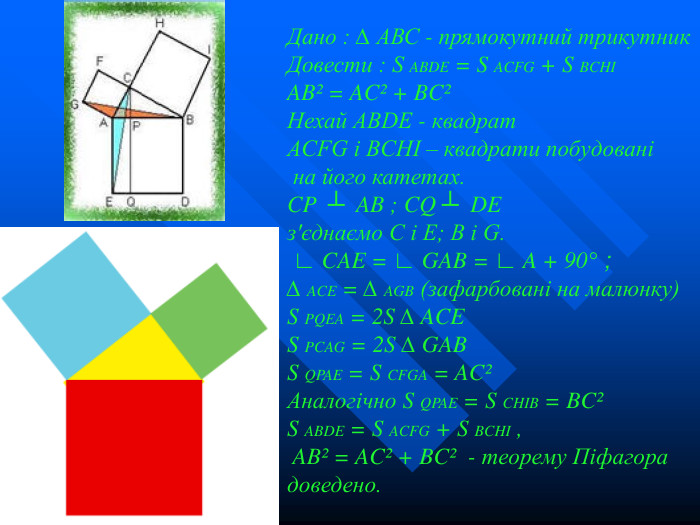
Дано : ∆ АВС - прямокутний трикутник Довести : S ABDE = S ACFG + S BCHI ABІ = ACІ + BCІ Нехай ABDE - квадрат ACFG і BCHI – квадрати побудовані на його катетах. CP ┴ AB ; CQ ┴ DE з'єднаємо C і E; B і G. ∟ CAE = ∟ GAB = ∟ A + 90° ; ∆ ACE = ∆ AGB (зафарбовані на малюнку) S PQEA = 2S ∆ ACE S PCAG = 2S ∆ GAB S QPAE = S CFGA = ACІ Аналогічно S QPAE = S CHIB = BCІ S ABDE = S ACFG + S BCHI , ABІ = ACІ + BCІ - теорему Піфагора доведено.

На протилежних берегах річки стоять двоє стрільців. Зріст одного 180 см, другого 120 см. Ширина річки 500 см. Обидва стрільці одночасно випускають стрілу з лука, влучаючи в один момент у мішень на поверхні води, що лежить на прямій, яка сполучає ступні стрільців. Знайти довжини шляхів стріл та місце знаходження мішені. Задача Розв’язок: Нехай АС = х см, тоді СК = (500 - х) см. ∆ АВС: ВС2 = 1802 + х2, ∆ СКМ:СМ2 = (500 - х) 2 + 1202. Оскільки стріли попали в ціль одночасно, то СМ = ВС 1802 + х2 = (500 - х) 2 + 1202; х = 232. Таким чином, відстань до мішені 232 см, а довжина шляху стріли ВС2 = 1802 + 2322 = 86 224, ВС ≈ 294 см. Відповідь: 294 см, 232 см. А В М К С

32 + 42 = 52 52 + 122 = 132 72 + 242 = 252 92 + 402 = 412 112 + 602 = 612 132 + 842 = 852 62 + 82 = 102 92 + 122 = 152 122 + 162 = 202 Трикутник зі сторонами 3, 4 і 5 часто називають Єгіпетським трикутником. Піфагорові трійки m2 - n2 m2 + n2 2 m n

Заповніть порожні клітинки таблиці

С В А К Дано : Рівнобедрений трикутник ABC AB = BC = 50 м, AC = 28 м BK – медіана Знайти : Довжину BK АК = КС = 14 м АB2 = BK2 + AK2 BK2 = АB2 - AK2 BK2 = 502 - 142 = 2500 – 196 =2304 BK = 48 м Задача

Визначте, чи є прямокутним трикутник зі сторонами: Розв’яжіть задачу Дано Знайти: РABCD