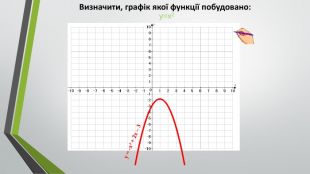
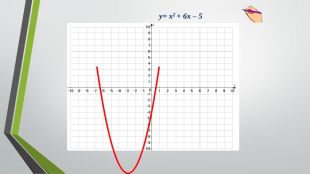
Презентація на урок алгебри у 9 класі з теми: "Квадратична нерівність"
Про матеріал
Дану презентацію можна використовувати на урок алгебри у 9 класі при закріпленні теми "Квадратичні нерівності"
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





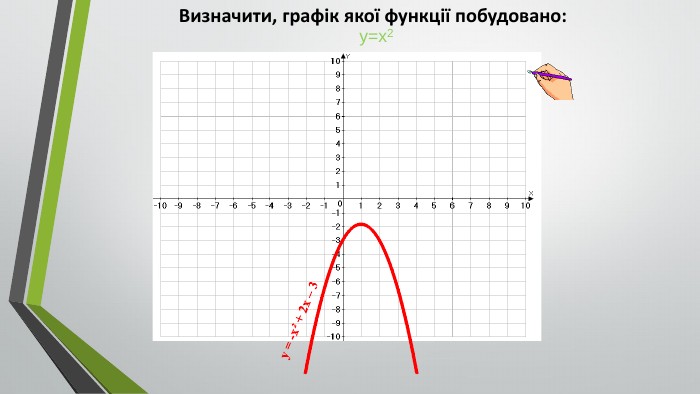
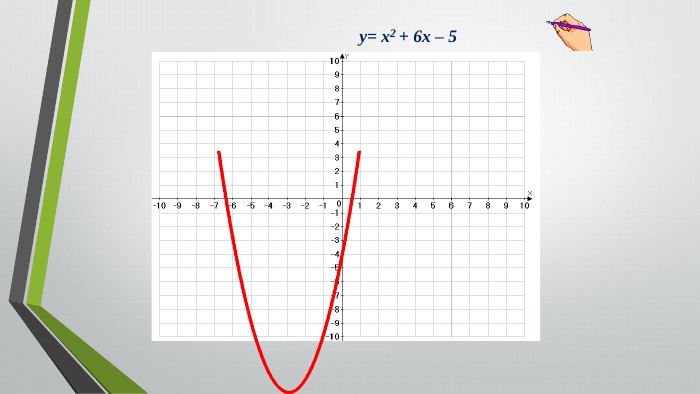



![1. Розглянемо функцію у=-х2+8х-12. 3. Нулі функції: -х2+8х-12=0 Відповідь:4. Ескіз графіка функції///////////////////2. Графіком функції є парабола, вітки якої напрямлені вниз, оскільки а=-1, -1<0.y≥0 , якщо x Є[2;6]x26[2;6]Розв'язати нерівність - x2 +8x-12 ≥ 0 Розв'язання 1. Розглянемо функцію у=-х2+8х-12. 3. Нулі функції: -х2+8х-12=0 Відповідь:4. Ескіз графіка функції///////////////////2. Графіком функції є парабола, вітки якої напрямлені вниз, оскільки а=-1, -1<0.y≥0 , якщо x Є[2;6]x26[2;6]Розв'язати нерівність - x2 +8x-12 ≥ 0 Розв'язання](/uploads/files/4663/305127/331956_images/10.jpg)