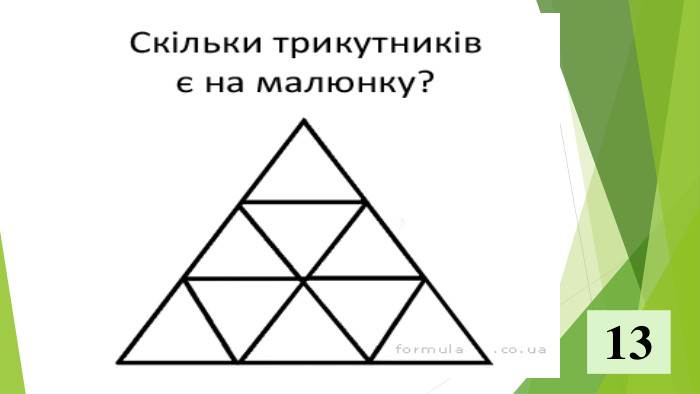
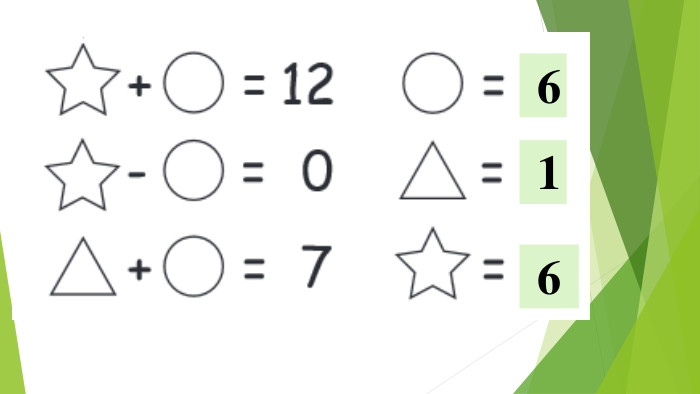
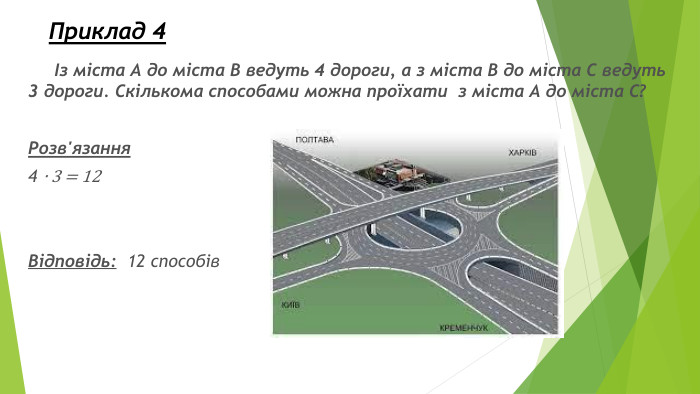
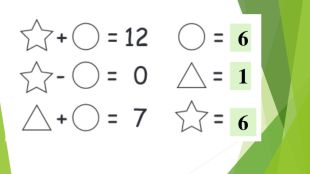
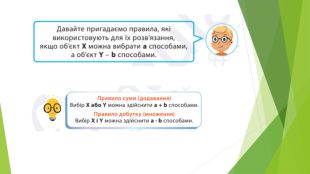
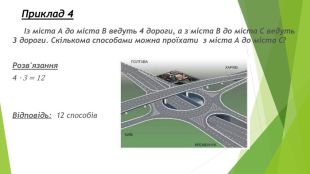
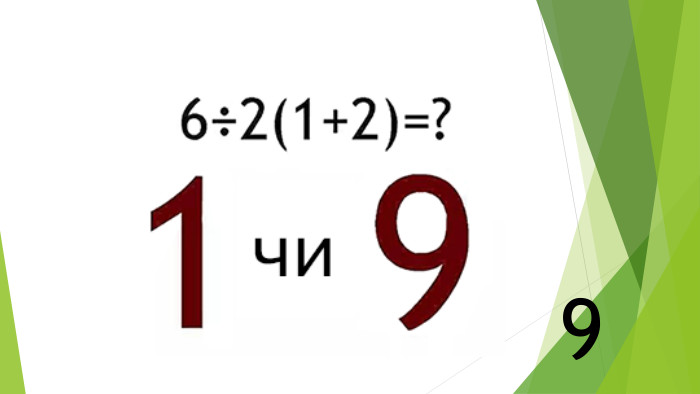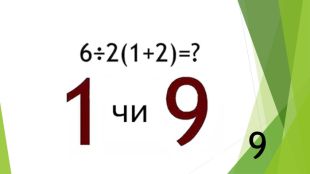Презентація "Найпростіші комбінаторні задачі"
Про матеріал
Урок ознайомлення з новим матеріалом , містить логічні завдання які налаштовують на роботу, пояснення та розв'язання задач, рефлексію. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку