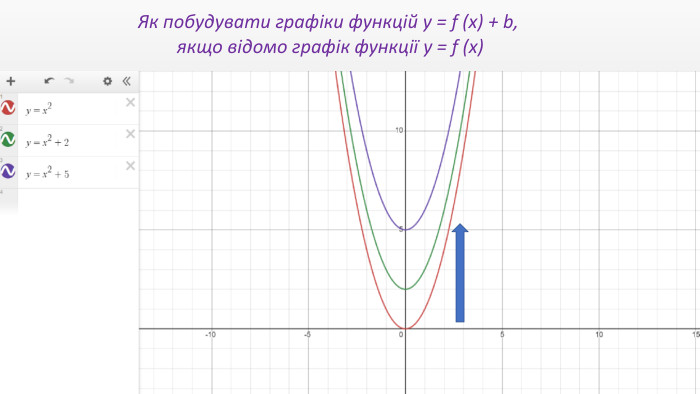
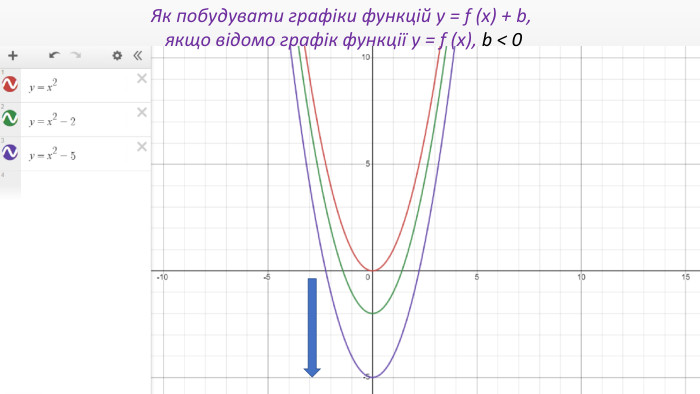
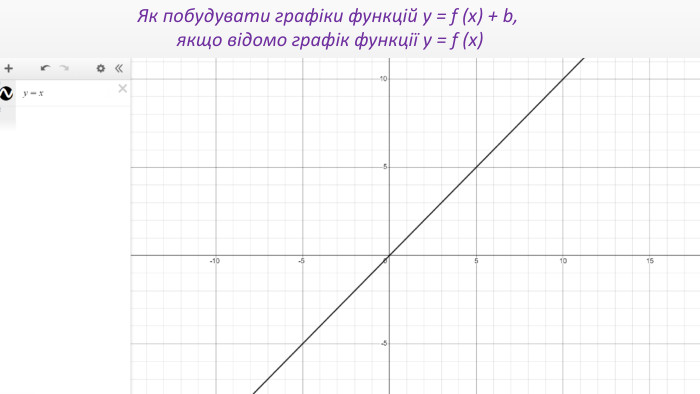
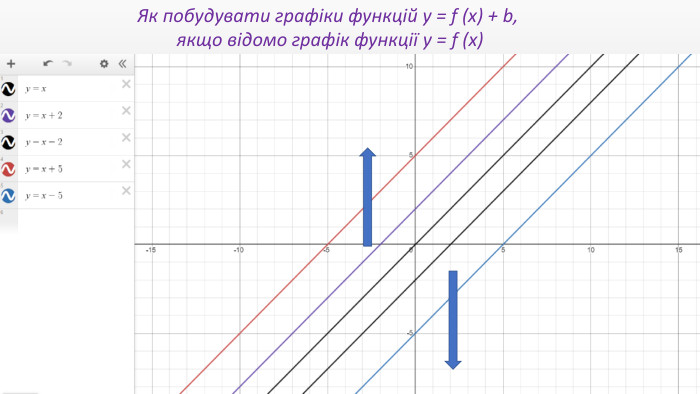
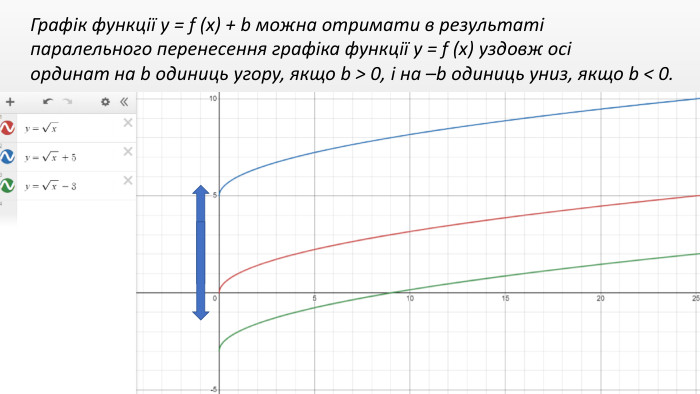
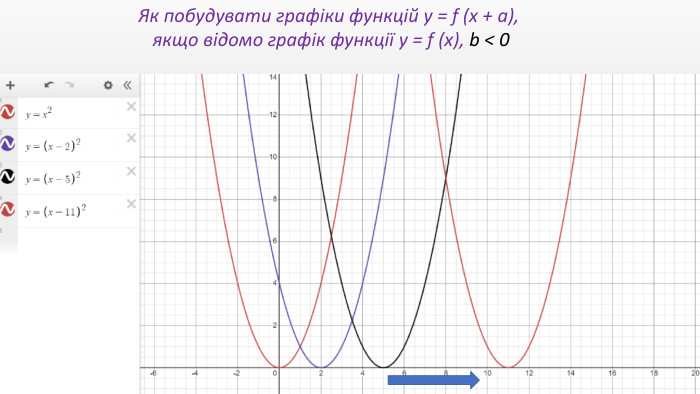
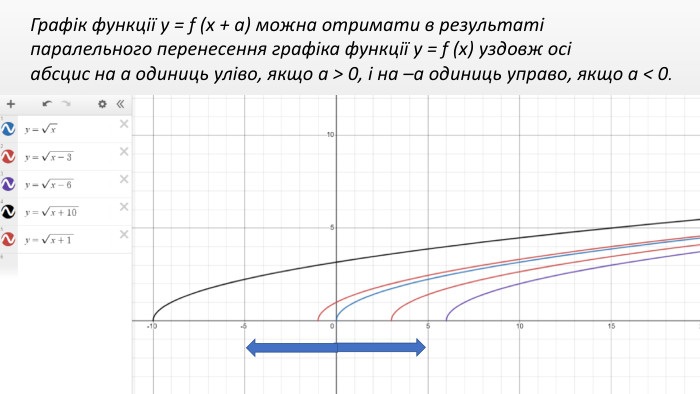
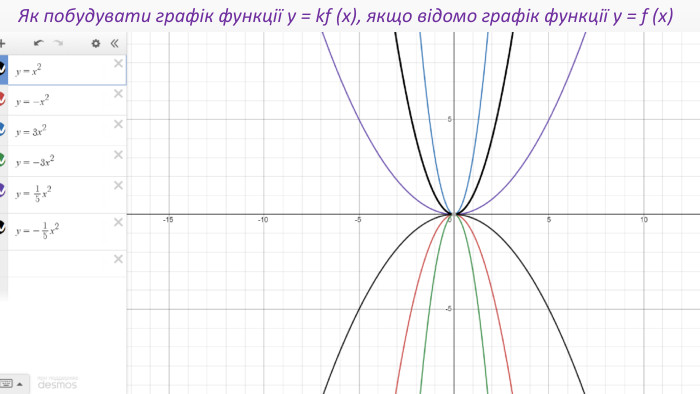
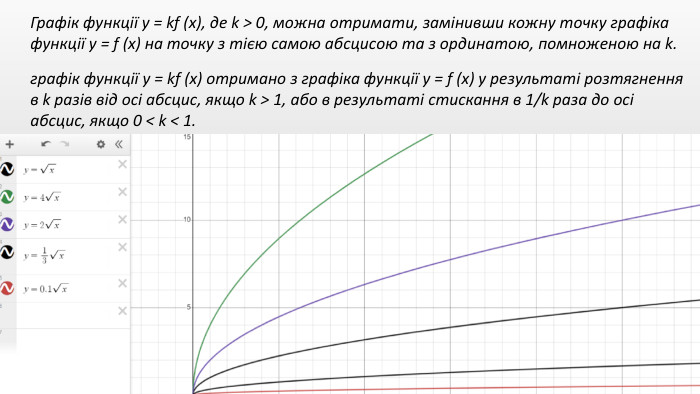
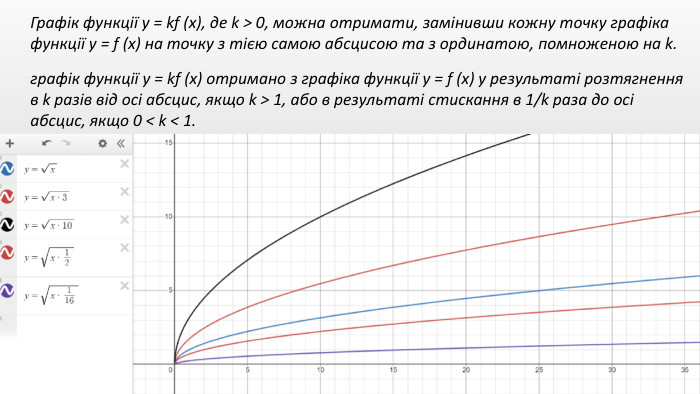
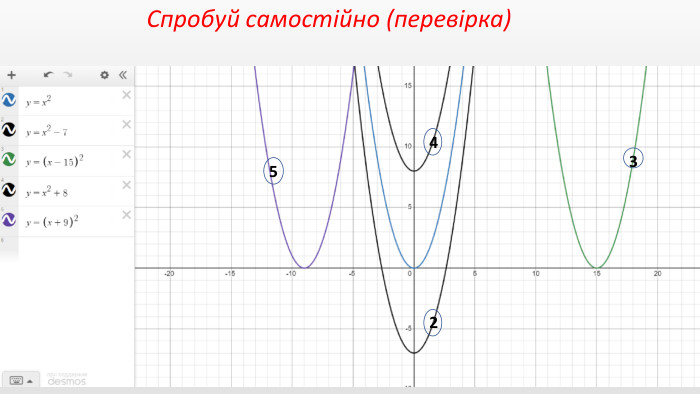
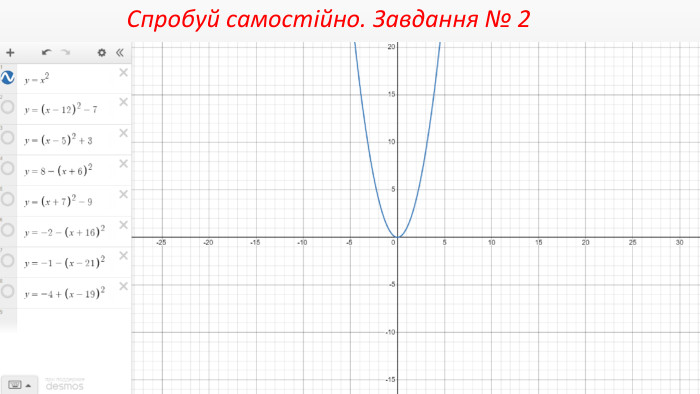
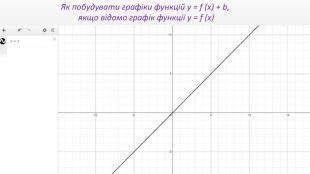
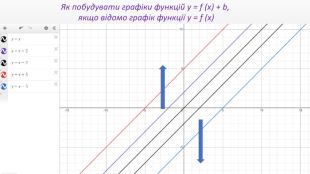
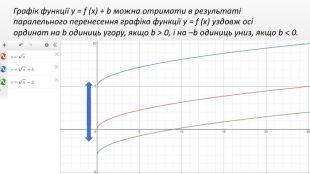
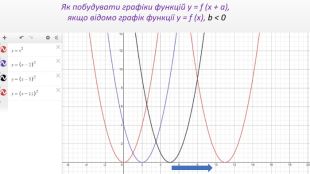
Презентація "Перетворення графіків функцій"
Про матеріал
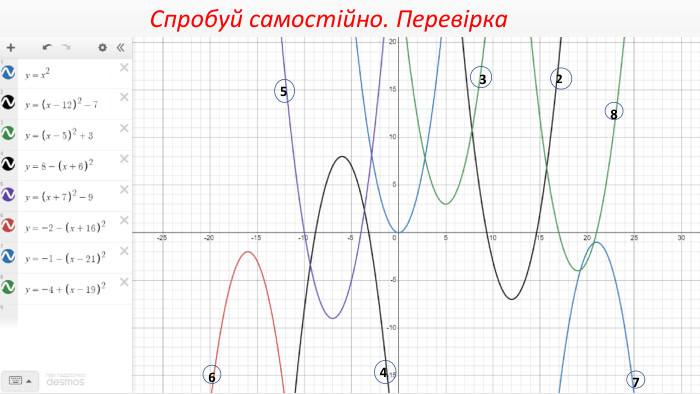
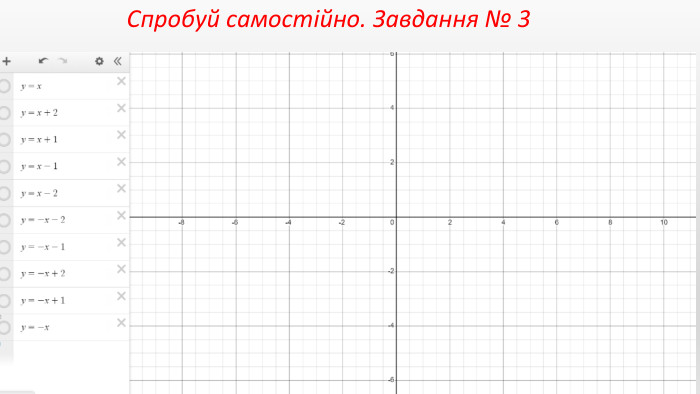
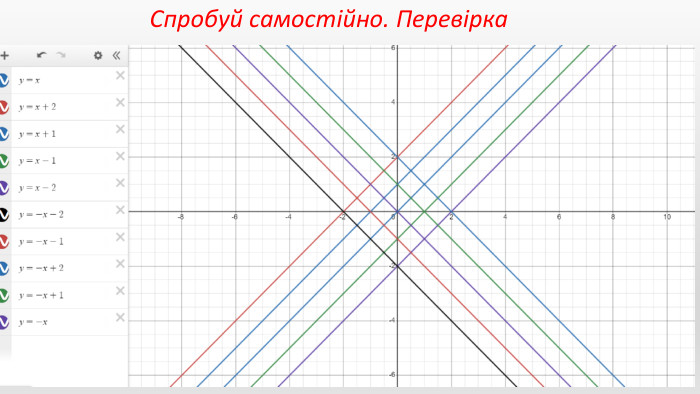
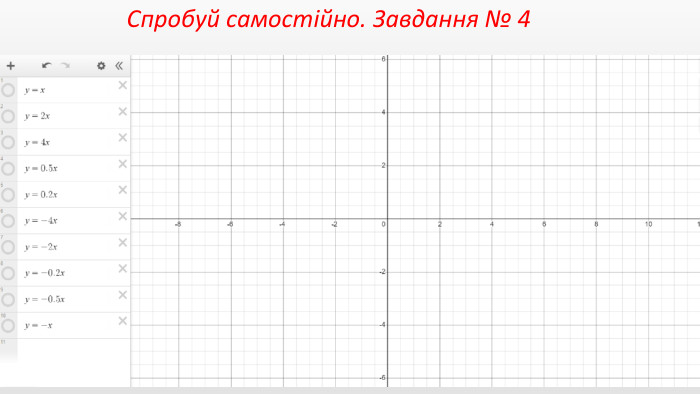
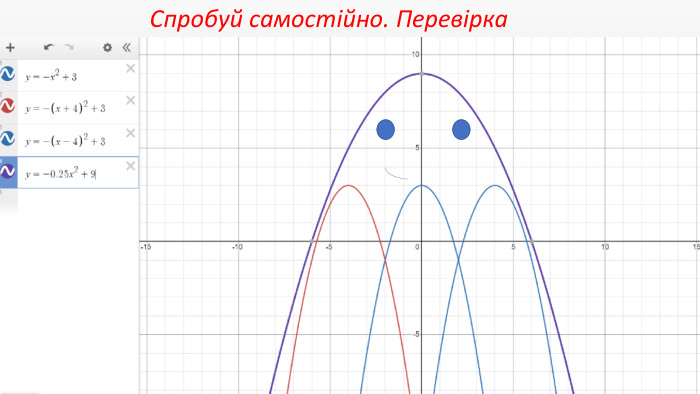
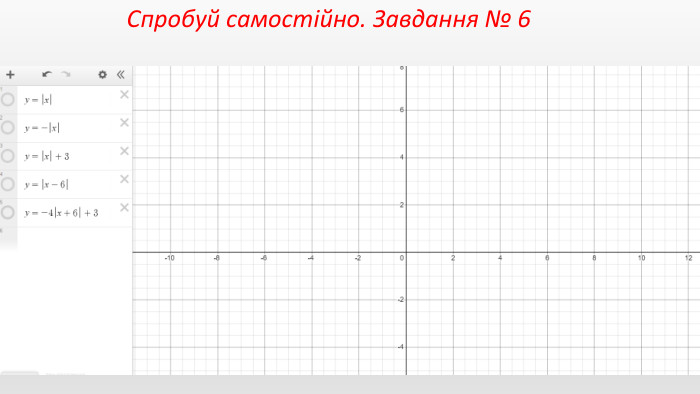
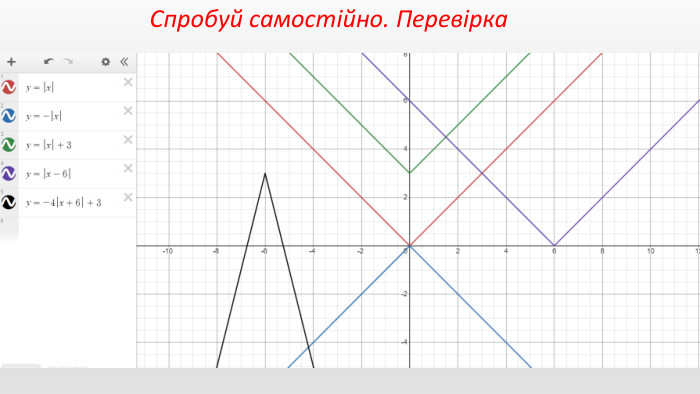
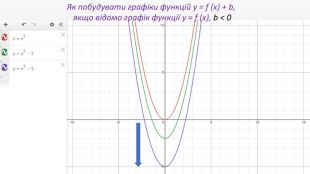
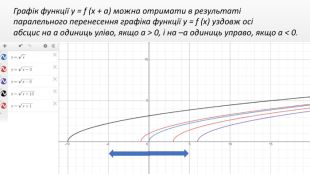
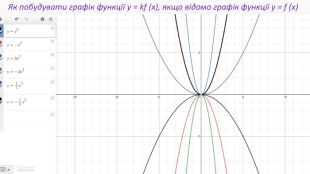
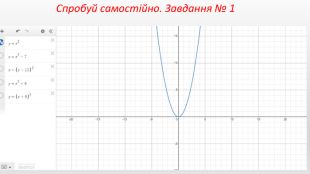
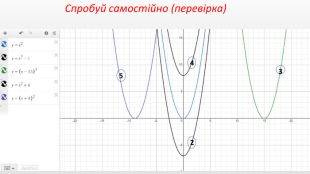
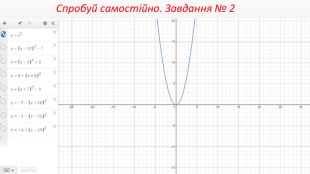
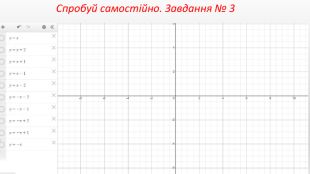
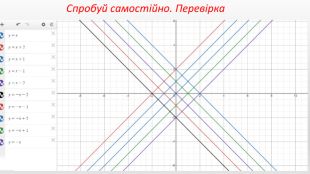
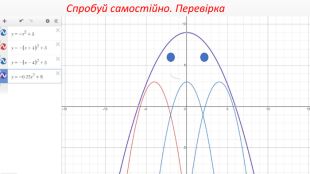
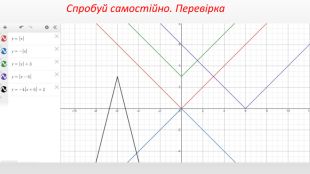
Презентація створення для опрацювання теми - Правила перетворення графіків функцій. Містить наочний матеріал і вправи для закріплення Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку